Статья опубликована в рамках: XXVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 04 февраля 2015 г.)
Наука: Математика
Секция: Математическая физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ЭНЕРГИЯ ВИХРЕВЫХ РАСПРЕДЕЛЕНИЙ НАМАГНИЧЕННОСТИ ЛЕГКОПЛОСКОСТНОГО ФЕРРОМАГНЕТИКА
Хусаинова Галина Владимировна
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E -mail: aldisa@mail.ru
Хусаинов Дамир Зиннурович
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E -mail: damiran@mail.ru
Сагарадзе Игорь Викторович
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E-mail:
THE ENERGY OF VORTEX MAGNETIZATION DISTRIBUTIONS IN EASY-PLANE FERROMAGNET
Khusainova Galina
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
Khusainov Damir
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
Sagaradze Igor
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
АННОТАЦИЯ
Рассмотрена энергия легкоплоскостного ферромагнетика с вихревым статическим распределением намагниченности, образующегося при взаимодействии двух ![]() доменных границ. Проведен анализ зависимости энергии от взаимного расположения границ. Показано, что энергия имеет наименьшее значение в случае, когда доменные границы параллельны .
доменных границ. Проведен анализ зависимости энергии от взаимного расположения границ. Показано, что энергия имеет наименьшее значение в случае, когда доменные границы параллельны .
ABSTRACT
The energy of vortex static magnetization distribution in easy-plane ferromagnet arising by interaction two ![]() domain walls was considered. The analysis of dependence energy from relative position walls has been done. It has been shown that energy is least value in the case of parallel domain walls.
domain walls was considered. The analysis of dependence energy from relative position walls has been done. It has been shown that energy is least value in the case of parallel domain walls.
Ключевые слова: вихрь; солитон; энергия ферромагнетика.
Keywords: vortex; soliton; energy of ferromagnet.
Теоретические исследования стационарных неоднородных распределений намагниченности основываются на определенных физических приближениях [2, c. 27]. При этом нелинейные уравнения феноменологической теории магнетизма сводятся к более простым уравнениям, имеющим точные аналитические решения. Так, для модели ферромагнетика с большой анизотропией по оси Z: ![]() и
и ![]() (
(![]() — постоянные анизотропии) двумерные распределения вектора намагниченности
— постоянные анизотропии) двумерные распределения вектора намагниченности ![]() описываются нелинейным двумерным статическим уравнением синус-Гордон [2, c. 96]:
описываются нелинейным двумерным статическим уравнением синус-Гордон [2, c. 96]:
![]() (1)
(1)
где ![]() — азимутальный угол,
— азимутальный угол, ![]() ,
,
![]() — характерная магнитная длина, связанная с обменным взаимодействием и постоянной анизотропии:
— характерная магнитная длина, связанная с обменным взаимодействием и постоянной анизотропии: 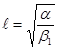 . В основном состоянии вектор намагниченности
. В основном состоянии вектор намагниченности ![]() лежит в «легкой плоскости» XY:
лежит в «легкой плоскости» XY: ![]() .
.
В этом случае плотность свободной энергии имеет вид:
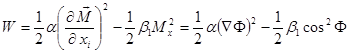 (i=1,2), (2)
(i=1,2), (2)
![]() — константа обменного взаимодействия.
— константа обменного взаимодействия.
Рассмотрим двухсолитонное решение уравнения (1) [1, c. 469] :
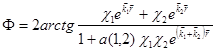 , (3)
, (3)
где ![]() ,
, ![]() — начальная фаза,
— начальная фаза, ![]() ,
, ![]() (i=1,2) ,
(i=1,2) ,
![]() ,
,![]() — вещественные постоянные,
— вещественные постоянные, ![]() .
.
Оно описывает вихревое распределение намагниченности, образующееся при пересечении двух 1800 доменных границ с топологическим зарядом n=2 [1, с. 470] .Для ограниченных фазовых постоянных ![]() (i=1,2) данное решение в пределе
(i=1,2) данное решение в пределе ![]() сводится к односолитонному решению. Нетривиальное решение нового типа (вырожденное солитонное решение) можно получить в пределе
сводится к односолитонному решению. Нетривиальное решение нового типа (вырожденное солитонное решение) можно получить в пределе ![]() , если рассматривать фазовые постояные неограниченными и имеющими особенности [3, с. 36]. Предположим, что фазовые постоянные являются сингулярными функциями параметров солитона:
, если рассматривать фазовые постояные неограниченными и имеющими особенности [3, с. 36]. Предположим, что фазовые постоянные являются сингулярными функциями параметров солитона:
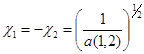 . (4)
. (4)
Преобразуем (3) :
![]() .
.
Пусть ![]() , где a и b — вещественные постоянные. Учитывая, что
, где a и b — вещественные постоянные. Учитывая, что ![]() , получаем
, получаем
![]() ,
, ![]() ,
, ![]() .
.
Таким образом, ![]() . (5)
. (5)
Или
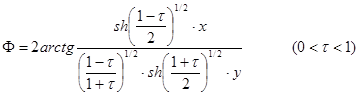 . (6)
. (6)
С учетом плотности энергии ферромагнетика W, магнитная энергия ферромагнетика:
![]() (7)
(7)
(выражение записано в безразмерных единицах, за единицу длины выбрана длина ![]() ) .
) .
С учетом (6) преобразуем данное выражение
![]() , (8)
, (8)
где ![]() — энергия основного состояния ферромагнетика,
— энергия основного состояния ферромагнетика,
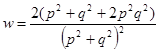 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Видно, что энергия (8) зависит от параметра ![]() . Отметим, что в работе [4, с. 22] авторами было исследовано простейшее вырожденное солитонное решение уравнения (1).Было показано, что в вырожденном случае, когда вектора
. Отметим, что в работе [4, с. 22] авторами было исследовано простейшее вырожденное солитонное решение уравнения (1).Было показано, что в вырожденном случае, когда вектора ![]() и
и ![]() , характеризующие доменные границы, параллельны (параметр
, характеризующие доменные границы, параллельны (параметр ![]() ) энергия ферромагнетика, хотя и большая (линейная по R), но меньше, чем в невырожденном случае с распределением намагниченности, соответствующим случаю перпендикулярных векторов
) энергия ферромагнетика, хотя и большая (линейная по R), но меньше, чем в невырожденном случае с распределением намагниченности, соответствующим случаю перпендикулярных векторов ![]() и
и ![]() (параметр
(параметр ![]() ). Этот анализ энергии для двух случаев расположения векторов:
). Этот анализ энергии для двух случаев расположения векторов: ![]() (вырожденный случай) и
(вырожденный случай) и ![]() позволяет предположить, что энергия ферромагнетика с уменьшением параметра
позволяет предположить, что энергия ферромагнетика с уменьшением параметра ![]() от 1 до 0 будет расти.
от 1 до 0 будет расти.
Исследуем изменение p и q как функций от параметра ![]() :
:
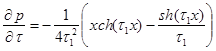 , (9)
, (9)
 . (10)
. (10)
Нетрудно показать, что в случае больших x и y; то есть при ![]() (A, B — некоторые числа):
(A, B — некоторые числа):
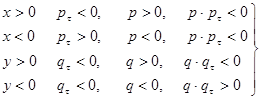 (11)
(11)
Найдем, как изменяется плотность энергии ![]() с изменением параметра
с изменением параметра ![]() :
:
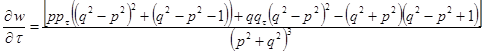 .(12)
.(12)
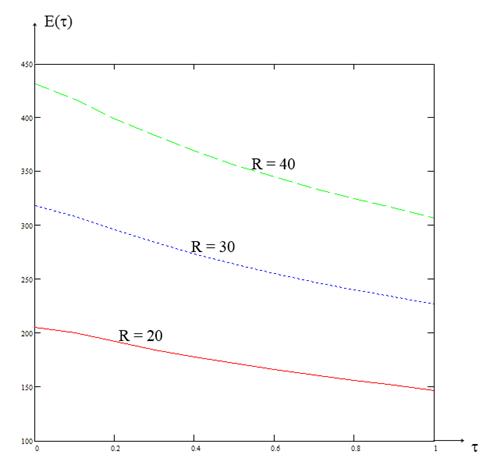
Рисунок 1. Зависимость энергии ![]() при различных значениях R (R = 20,30, 40). (R — размер образца)
при различных значениях R (R = 20,30, 40). (R — размер образца)
Внимательный анализ полученного выражения (12) с учетом (11) и того факта, что ![]() , приводит к результату:
, приводит к результату: ![]() . Таким образом, плотность энергии является убывающей функцией параметра
. Таким образом, плотность энергии является убывающей функцией параметра ![]() . Численный анализ интеграла энергии (8) дает аналогичный результат. На (рис. 1) приведена зависимость
. Численный анализ интеграла энергии (8) дает аналогичный результат. На (рис. 1) приведена зависимость ![]() для различных значений образца R. Видно, что для всех R наблюдается уменьшение величины энергии при увеличении значения
для различных значений образца R. Видно, что для всех R наблюдается уменьшение величины энергии при увеличении значения ![]() : при
: при ![]() энергия уменьшается, что полностью согласуется с результатом выше приведеннного аналитического анализа.
энергия уменьшается, что полностью согласуется с результатом выше приведеннного аналитического анализа.
Список литературы.
1.Борисов А.Б., Танкеев А.П., Шагалов А.Г. Вихри и двумерные солитоны в легкоплоскостных магнетиках //ФММ, — 1985 — Т. 60 — С. 468—479.
2.Косевич А.М., Иванов Б.А., Ковалев А.С. Нелинейные волны намагниченности. Динамические и топологические солитоны. Киев: Наук. Думка, 1983 — 192 с.
3.Хусаинова Г.В. (Безматерных Г.В.), Хусаинов Д.З. Вырожденное солитонное решение двумерного уравнения синус-Гордон //Фундаментальные и прикладные исследования в современном мире: материалы VII Междунар. науч.-практ. конф. СПб., — 2014 — Т. 1 — С. 32—38.
4.Хусаинова Г.В. (Безматерных Г.В.), Хусаинов Д.З. Вихревое решение двумерного уравнения синус-Гордон//Естественные и математические науки в современном мире: Cб. ст. по материалам XXVI Междунар. науч.-практ. конф. Новосибирск, — 2015 — № 1 (25) — С. 17—23.
дипломов


Оставить комментарий