Статья опубликована в рамках: XXVI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 12 января 2015 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
КОРРЕКТНОСТЬ ОДНОЙ ЛИНЕЙНОЙ НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ О НАСЫЩЕННО-НЕНАСЫЩЕННОЙ ФИЛЬТРАЦИИ
Семенко Евгений Вениаминович
д-р физ.-мат. наук, зав. кафедрой математического анализа, профессор Новосибирского государственного педагогического университета, РФ, г. Новосибирск
E -mail: semenko
Семенко Татьяна Ивановна
канд. физ.-мат. наук, доцент Новосибирского государственного педагогического университета, РФ, г. Новосибирск
CORRECTNESS OF ONE LINEAR INITIAL-BOUNDARY VALUE PROBLEM OF SATURATED-UNSATURATED FILTRATION
Evgeny Semenko
doctor of science, head of mathematical analysis department, professor of Novosibirsk State Pedagogical University, Russia, Novosibirsk
Tatyana Semenko
candidate of science, assistant professor of Novosibirsk State Pedagogical University, Russia, Novosibirsk
АННОТАЦИЯ
Рассматривается линейный аналог начально-краевой задачи, возникающей в теории фильтрации при моделировании совместного движения влаги в зонах полного и неполного насыщения. Линейная задача представляет самостоятельный интерес как неклассическая начально-краевая задача со свободной границей, с необычным условием на свободной границе, отражающим способ сопряжения течений на границе зон полного и неполного насыщения. В работе приводится доказательство существования и единственности обобщенного решения этой задачи.
ABSTRACT
The linear analog of initial-boundary value problem arising in filtration theory at modeling of water in saturated and unsaturated zones coupled movement is considered. The linear problem has a separate interest as non-classical free boundary problem with unusual conjugation condition on free boundary, reflecting the manner of conjugation of flows on the boundary of saturated and unsaturated zones. The proof of existence and uniqueness of generalized solution is brought in this work.
Ключевые слова: теория фильтрации; зона полного насыщения; зона неполного насыщения; задачи со свободными границами; обобщенное решение; теорема существования и единственности.
Keywords: filtration theory, saturated zone; unsaturated zone; free boundary problem; generalized solution; existence anduniqueness theorem.
Для описания взаимосвязанного движения влаги в зонах полного и неполного насыщения в [1] была предложена приближенная гидравлическая модель фильтрации, основанная на предположении о преобладании вертикальных потоков влаги в зоне неполного насыщения и горизонтальных — в зоне полного насыщения. Эта модель в случае профильной (происходящей в вертикальной плоскости) фильтрации представляет собой начально-краевую задачу для уравнения
|
|
(1) |
в области ![]() (зоне неполного насыщения грунта) со свободной границей
(зоне неполного насыщения грунта) со свободной границей ![]() , где
, где ![]() — глубина залегания грунтовых вод. Здесь
— глубина залегания грунтовых вод. Здесь ![]() — давление влаги в зоне неполного насыщения,
— давление влаги в зоне неполного насыщения, ![]() — одномерная фиксированная область. На свободной границе
— одномерная фиксированная область. На свободной границе ![]() задаётся условие
задаётся условие
|
|
(2) |
следующее из соотношения баланса влаги для всей толщи грунта и связывающее вертикальные потоки в зоне неполного насыщения с горизонтальными в зоне полного насыщения.
В работе [2] приводится линейная задача, полученная из исходной гидравлической модели путём сведения её к задаче в постоянной области с помощью замены переменной ![]() , а также фиксирования коэффициентов во всех уравнениях и граничных условиях. Эта задача отражает главные особенности исходной модели — предположения о преобладании вертикальных скоростей в зоне неполного насыщения, горизонтальных скоростей в зоне полного насыщения, а также способ сопряжения этих двух зон. Мы приведём здесь развернутое доказательство существования и единственности обобщенного решения линейной задачи.
, а также фиксирования коэффициентов во всех уравнениях и граничных условиях. Эта задача отражает главные особенности исходной модели — предположения о преобладании вертикальных скоростей в зоне неполного насыщения, горизонтальных скоростей в зоне полного насыщения, а также способ сопряжения этих двух зон. Мы приведём здесь развернутое доказательство существования и единственности обобщенного решения линейной задачи.
Итак, рассмотрим полученную в [2] задачу для функций ![]() и
и
![]() :
:
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
где: ![]() — постоянная,
— постоянная, ![]() ,
,
![]() ,
,
![]() — положительные постоянные.
— положительные постоянные.
Определение. Обобщенным решением задачи (3)—(7) в ![]() назовём пару функций (w, h) таких, что
назовём пару функций (w, h) таких, что
![]()
|
|
|
удовлетворяющих условиям:
|
1) |
(8) |
|
|
|
|
|
|
|
2)
|
(9) |
|
3)
|
(10) |
Здесь![]() ,
, ![]() ,
, ![]()
Теорема. Пусть в условии (5) ![]() Тогда существует единственное обобщенное решение (w, h) задачи (3)—(7), причём справедлива оценка:
Тогда существует единственное обобщенное решение (w, h) задачи (3)—(7), причём справедлива оценка:
|
|
(11) |
Доказательство. Для доказательства существования решения применим метод Фурье. Будем отыскивать частное решение уравнения (3) в виде
![]() (12)
(12)
и потребуем, чтобы оно удовлетворяло условиям (4), (6), (7). Подставляя (12) в (3), (4), (6), (7), получим следующие краевые задачи для функций ![]() и уравнение для
и уравнение для ![]() :
:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
где ![]() — постоянные.
— постоянные.
Уравнение (15) при любом ![]() имеет решение
имеет решение ![]() , где
, где ![]() Задача (13) разрешима при
Задача (13) разрешима при ![]() где
где ![]() ,
, ![]() соответствующие решения имеют вид:
соответствующие решения имеют вид: ![]() . Задача (14) для любого фиксированного
. Задача (14) для любого фиксированного ![]() разрешима при
разрешима при ![]() ,
, ![]() , где
, где ![]() , а
, а ![]() являются положительными решениями уравнения
являются положительными решениями уравнения ![]() ctg
ctg![]() ; соответствующие решения имеют вид
; соответствующие решения имеют вид ![]() y. Решения задач Штурма-Лиувилля (13), (14) образуют полные ортогональные системы в
y. Решения задач Штурма-Лиувилля (13), (14) образуют полные ортогональные системы в ![]() и
и ![]() соответственно, следовательно, система функций
соответственно, следовательно, система функций ![]() является полной ортогональной системой в
является полной ортогональной системой в ![]() .
.
Обозначим через ![]() коэффициенты разложения функции
коэффициенты разложения функции ![]() в ряд Фурье по этой системе:
в ряд Фурье по этой системе:

и пусть ![]() =
=![]() Как известно,
Как известно, ![]() в
в ![]() при
при ![]() и справедлива оценка
и справедлива оценка
![]() (16)
(16)
(неравенство Бесселя). Пусть теперь
![]() =
=![]() (17)
(17)
Нетрудно заметить, что ![]() является решением задачи
является решением задачи
![]() , (3*)
, (3*)
![]() (4*)
(4*)
![]() (5*)
(5*)
![]() (6*)
(6*)
![]() (7*)
(7*)
Покажем, что для ![]() справедлива оценка
справедлива оценка
![]() (11*)
(11*)
где ![]() есть некоторая постоянная, не зависящая от
есть некоторая постоянная, не зависящая от ![]() Для этого умножим (3*) на
Для этого умножим (3*) на ![]() и проинтегрируем равенство по
и проинтегрируем равенство по ![]() ,
,![]()
![]() +
+![]() (18)
(18)
=![]()
Принимая во внимание (4*), (6*), (7*), получаем:
I=![]() (19)
(19)
= ![]()
C учётом (18) и (19) имеем:
![]() (20)
(20)
где ![]() не зависит от
не зависит от ![]() откуда, переходя к максимуму по
откуда, переходя к максимуму по ![]() , мы и получаем требуемую оценку (11*).
, мы и получаем требуемую оценку (11*).
Далее, с учётом (16), имеем:
G(![]() )
)![]() , (21)
, (21)
что означает равномерную по ![]() ограниченность последовательностей
ограниченность последовательностей ![]() в
в ![]() . Следовательно, существует подпоследовательность (сохраним для неё обозначение
. Следовательно, существует подпоследовательность (сохраним для неё обозначение ![]() ) такая, что
) такая, что ![]() слабо в
слабо в ![]() Так как
Так как ![]() очевидно, удовлетворяет (8)
очевидно, удовлетворяет (8)![]() , то, переходя в этих тождествах к пределу при
, то, переходя в этих тождествах к пределу при ![]() , получим, что
, получим, что ![]() обобщённое решение задачи (3)
обобщённое решение задачи (3)![]() с начальным значением
с начальным значением ![]() , и для него справедлива оценка (11) как для слабого предела последовательности
, и для него справедлива оценка (11) как для слабого предела последовательности ![]() этой оценке удовлетворяющей. Существование обобщенного решения доказано.
этой оценке удовлетворяющей. Существование обобщенного решения доказано.
Докажем теперь единственность такого решения. Пусть ![]() два обобщённых решения задачи (3)
два обобщённых решения задачи (3)![]() , и пусть
, и пусть ![]() Тогда
Тогда ![]() является обобщённым решением задачи при
является обобщённым решением задачи при ![]() Заметим, что так как
Заметим, что так как ![]() , то равенство (8) справедливо для любой функции
, то равенство (8) справедливо для любой функции ![]() такой, что
такой, что ![]() ,
, ![]() (множество
(множество ![]() плотно в классе таких функций).
плотно в классе таких функций).
Рассмотрим в ![]() функцию
функцию
|
|
(22) |
Нетрудно убедиться, что ![]() имеет в
имеет в ![]() обобщённые производные
обобщённые производные ![]() принадлежащие
принадлежащие ![]() Далее, так как
Далее, так как ![]() то при почти всех
то при почти всех ![]() существует значение
существует значение ![]() , причём, с учётом (11),
, причём, с учётом (11), ![]() при почти всех
при почти всех ![]()
Из свойств функции ![]() заключаем, что функция
заключаем, что функция ![]() имеет обобщённую производную
имеет обобщённую производную ![]() принадлежащую
принадлежащую ![]() и
и ![]() Подставив функцию
Подставив функцию ![]() вида (22) в тождество (8) с
вида (22) в тождество (8) с ![]() получим равенство
получим равенство
|
+ |
(23) |
Легко проверить, что для любой функции ![]()
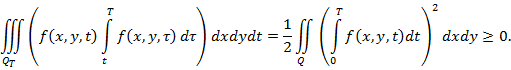
Следовательно, второе и третье слагаемые в (23) неотрицательны, поэтому ![]() откуда вытекает, что
откуда вытекает, что ![]() в
в ![]() то есть
то есть ![]() .
.
Далее, так как ![]() , то
, то ![]() в
в ![]() , то есть
, то есть ![]() что завершает доказательство единственности решения.
что завершает доказательство единственности решения.
Список литературы:
1.Антонцев С.Н., Епихов Г.П., Кашеваров А.А. Системное математическое моделирование процессов водообмена. Новосибирск: Наука, 1986. — 216 с.
2.Семенко Т.И. О корректности приближенной гидравлической модели насыщенно-ненасыщенной фильтрации // Динамика сплошной среды. Новосибирск, — 1991. — Вып. 102. — С. 114—132.
дипломов


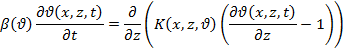
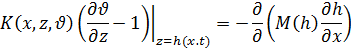
Оставить комментарий