ЧИСЛОВАЯ ОЦЕНКА ЭФФЕКТИВНОСТИ И РАНЖИРОВАНИЕ БППС СОТОВОЙ СВЯЗИ

Хакимов Рахматджон Иномович

преподаватель Худжандского государственного университета им. академика Б. Гафурова, Республика Таджикистан, г. Худжанд

E-mail: rahmatjon at gmail.com

NUMERICAL EVALUATION OF EFFICIENCY AND RANKING OF CELLULAR NETWORK’S BTSS

Hakimov Rahmatjon

teacher at Khujand State University named after academician B. Gafurov, Republic of Tajikistan, Khujand

АННОТАЦИЯ

В статье рассматривается вопрос об оценке качества обслуживания телефонных звонков абонентов сотовой связи. Вводится числовая характеристика — вес базовой приемопередающей станции в итоговой доле дефектных звонков. Приводится алгоритм, который может быть использован для поддержки принятия решения по выбору БППС с целью проведения в них оптимизационных работ. Описываются преимущества и недостатки данного алгоритма. Приводятся примеры вычислений числовых оценок.

ABSTRACT

The problem of the evaluation of the quality of service for cellular communications subscribers’ phone calls is discussed in this paper. A numerical characteristic — the weight of a base transceiver station in the total rate of defective calls — is entered. An algorithm that can be used to support a decision making on the selection of the BTSs to provide the optimization works in them is given. Some of the advantages and disadvantages of this algorithm are described. Examples of calculation of numerical evaluations are provided.

Ключевые слова: числовая оценка; вес; БППС; сотовая связь; качество обслуживания; алгоритм; оптимизация; доля дефектных звонков.

Keywords: numerical evaluation; weight; BTS; cellular communications; quality of service; algorithm; optimization; defective calls ratio.

Введение. Популярность технологий сотовой связи второго (GSM) и третьего поколений (WCDMA), обусловленная возможностью предоставления качественных услуг мобильной телефонии, доступа в Интернет, видеоконференций и других, породила рынок с высоким уровнем конкуренции. Вопрос поддержания и улучшения качества работы сети сотовой связи важен, в связи с его непосредственным отношением к удовлетворенности абонента (клиента) работой оператора (поставщика услуг). Процесс выбора базовых приемопередающих станций (БППС [3, с. 24] или БС [1, с. 112]), в которых будут проводиться оптимизационные работы с целью улучшения качества работы сети, актуален по причине ограниченности ресурсов: технических, людских, временных и финансовых. В данной работе качество обслуживания телефонных звонков абонентов оператором сотовой связи оценивается на основе функционирования БППС сети оператора в определенный (конечный) промежуток времени.

Постановка задачи. Предполагается, что известны числа n_j, m_j, j=1,...,k, где k — общее количество БППС в сети оператора, n_j — общее количество звонков поступивших в j-ю станцию, m_j - количество дефектных звонков среди поступивших в j-ю станцию. Предполагается, что n_j > 0, j=1,...,k. Звонок считается дефектным, если произошел провал звонка [3, с.124] до первого гудка или обрыв звонка до отбоя.

По числам n_j, m_j, j=1,...,k требуется количественно оценить уровень обслуживания звонков станциями и на основе оценок разработать алгоритм, который позволит автоматизировать процесс выбора БППС для проведения в них оптимизационных работ. Алгоритм должен помогать в выборе таких БППС, улучшение работы которых даст наилучший эффект в уменьшении доли дефектных звонков в общем количестве звонков, произведенных в рассматриваемый промежуток времени. Следует отметить, что как параметр для улучшения могут быть выбраны различные ключевые показатели качества сети, например, доля успешности установки звонков (CSSR, Call Setup Success Rate) [6, с. 54] или доля обрывов звонков по трафиковому каналу (Call Drop Rate on TCH) [7, с. 57].

Введем следующие обозначения:

 — тотальное количество звонков,

 — тотальное количество дефектных звонков,

 — тотальная доля дефектных звонков,

 — доля дефектных звонков при обслуживании j-ой станцией.

Оптимальность работы БППС будем определять значением тотальной доли дефектных звонков . Чем меньше значение , тем эффективной считается работа станций в целом.

Определение. Значение , вычисляемое по следующей формуле, назовем весом j-й БППС в тотальной доле дефектных звонков:

I. Некоторые утверждения

Утверждение 1. Вес j-й БППС в тотальной доле дефектных звонков равен нулю, тогда и только тогда, когда доля дефектных звонков, поступивших в эту БППС, равна тотальной доле дефектных звонков:

Доказательство. Пусть для некоторой j-й БППС имеем  Тогда

Что и требовалось доказать.

Утверждение 2. Вес j-й БППС в тотальной доле дефектных звонков больше (меньше) нуля, тогда и только тогда, когда доля дефектных звонков, поступивших в эту БППС, больше (меньше) тотальной доли дефектных звонков:

Доказательство. Рассмотрим случай «больше». Пусть для некоторой j-й БППС имеем Тогда

Последнее неравенство верно в силу того, что  и

Далее,

Что и требовалось доказать.

Случай «меньше» доказывается аналогичным образом.

Утверждение 3. Не теряя общности, предположим, что  

Тогда и обратно.

Доказательство. Так как  и  при j = 1, …, k, то учитывая определение  имеем:

Что и требовалось доказать.

Интерпретировать утверждение 3 можно следующим образом. Предположим, что отключение 1-й БППС не отразится никак на количестве звонков, поступающих в другие БППС и на количестве дефектных звонков этих БППС. Тогда, если отключить 1-ю БППС, то тотальная доля дефектных звонков будет лучше, чем в случае отключения любой другой БППС. Но на практике так поступают крайне редко, так как каждая БППС: 1) обслуживает абонентов своей зоны покрытия, доставляя голосовой и пакетный трафик, этим принося доход [5, с. 63]. Следовательно, операторы заинтересованы в минимизации времени простоя БППС [8, с. 175]; 2) отключение одной БППС обычно повышает нагрузку на другие БППС, что, как правило, отражается плохо на показателях качества сети. Как частный случай, может ухудшиться показатель хендовера. Оператор понимает необходимость расходования ресурсов на уменьшение количества обрывов звонков [4, с. 169].

Поэтому задачу поставим иным образом: свести вес j-й БППС к нулю.

Пусть для некоторой j-й БППС имеет место: Из определения веса БППС в тотальной доле дефектных звонков следует, что для этой БППС имеет место

Предположим, что в результате работ на некоторой БППС:

1)  уменьшится количество дефектных звонков на этой БППС;

2)  количество звонков на этой и других БППС не изменится;

3)  количество дефектных звонков на других БППС не изменится.

Учитывая эти предположения, какое должно быть количество дефектных звонков на j-й БППС, чтобы её вес в тотальной доле дефектных звонков уменьшился в r раз?

Введем обозначение Тогда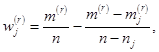

Где

Отсюда получаем

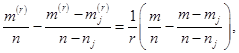
Имея в виду, что получаем

При сформулированных выше предположениях 1)—3) верно следующее

Утверждение 4. Количество дефектных звонков на j-й БППС должно равняться 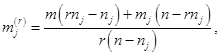чтобы её вес в тотальной доле дефектных звонков уменьшился в r раз.

Утверждение 5. При сведении количества дефектных звонков j-й БППС с m_j на :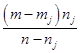

1)  тотальная доля дефектных звонков уменьшится с  на то есть на w_j;

2)  вес j-й БППС в тотальной доле дефектных звонков будет равен нулю.

Доказательство. Пусть

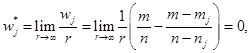
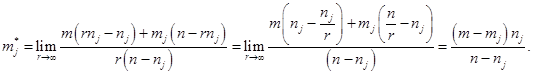
Предположим, что в результате работ на j-й БППС:

1)  количество звонков на этой и других БППС не изменилось;

2)  количество дефектных звонков на других БППС не изменилось;

3)  количество дефектных звонков на j-й БППС было сведено к

С одной стороны, доля дефектных звонков j-й БППС будет равна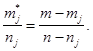 С другой стороны, имея в виду, что получаем

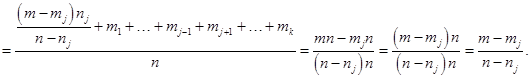
То есть тотальная доля дефектных звонков тоже будет равна

Что и требовалось доказать.

Следствие 1. При выборе в качестве объекта оптимизации БППС с наибольшим весом и при сформулированных выше предположениях 1)—3) сведение её веса к нулю даст наилучший эффект в уменьшении тотальной доли дефектных звонков.

Исходя из вышеизложенных утверждений и следствия 1, опишем искомый алгоритм.

II . Алгоритм для выбора БППС для оптимизации с целью уменьшения тотальной доли дефектных звонков

Предлагаем следующий алгоритм для выбора БППС для оптимизации с целью уменьшения тотальной доли дефектных звонков

1)  вычислить тотальную долю дефектных звонков;

2)  вычислить вес каждой БППС в тотальной доле дефектных звонков;

3)  выбрать БПС с максимальным весом (отсортировать по весу);

4)  уменьшить количество дефектных звонков выбранной БППС (с m_j на);

5)  пересчитать тотальную долю дефектных звонков;

6)  при необходимости перейти к п.2.

Пункты 1, 2, 5 алгоритма показывают, что на практике вычисления могут занимать значительные ресурсы памяти и процессора ЭВМ. Пункт 3 изложенного алгоритма показывает, что алгоритм может дать хороший результат в случае относительно неравномерного распределения дефектных звонков между различными БППС. Так, в случае оптимизации работы БППС, имеющего вес в разы больше остальных БППС, можно получить значительные улучшения показателя тотальной доли дефектных звонков. Если же дефектные звонки распределены относительно равномерно между всеми БППС, то веса различных БППС приблизительно равны нулю и оптимизация работы одной БППС не даст значительного улучшения показателя тотальной доли дефектных звонков. В связи с пунктом 4 возникает вопрос о технической возможности уменьшения дефектных звонков на БППС с высоким весом. Вполне вероятны случаи, когда невозможно уменьшить количество дефектных звонков на некоторой БППС в связи с особенностями рельефа местности, условий распространения радиосигнала и т. д.

В связи с пунктом 4 приведенного алгоритма актуален вопрос о возможности перераспределения нагрузок n₁, ..., n_k между станциями для уменьшения дефектных весов. При этом количества дефектных звонков , ,  могут меняться. Данный вопрос в некоторой степени рассмотрен в [2, с. 271].

III . Пример подсчета веса БППС до и после оптимизации

Есть понятие дефектов на миллион единиц (англ., Defects Per Million Opportunities, DPMO):

Для обозначения доли дефектных звонков далее воспользуемся аббревиатурой MCDR (англ., Mobile Call Defects Ratio).

В приведенной ниже таблице 1 наибольший вес в общем MCDR имеет БППС № 5 с весом 768 DPMO.

Общее количество звонков на БППС № 5 до оптимизации равно n₅ = 66751. Общее количество дефектных звонков на БППС № 5 до оптимизации равно m₅ = 1328+642 = 1970.

Общее количество звонков на сети до оптимизации равно n = 726687. Общее количество дефектных звонков на сети до оптимизации равно m =10604 + 5325 = 15929. Следовательно,

Предположим, что в результате оптимизационных работ на БППС № 5 (и сети, вообще) сохранилось количество попыток звонков, но уменьшилось количество дефектных звонков на БППС и достигло 1020+392=1412. Так её вес в тотальной доле дефектных звонков был сведен практически к нулю (при новом пересчете). В итоге, общее значение MCDR DPMO с 21920 DPMO уменьшилось до 21152 DPMO (убыло на 768 DPMO).

В таблицах 1-4 данные столбцов «MCDR, DPMO» и «БППС, DPMO» округлены до целого.

Таблица 1.

Данные по 10-и БППС до оптимизации

Таблица 2.

Итоговые данные по 10-и БППС до оптимизации

Таблица 3.

Данные по 10-и БППС после оптимизации

Таблица 4.

Итоговые данные по 10-и БППС после оптимизации

После рассмотренного шага оптимизации наибольший вес имеет БППС № 9.

Построим две диаграммы рассеяний для данных до оптимизации (до сведения веса БППС № 5 к нулю) и после на основе двух показателей: доли дефектных звонков и количества попыток звонков каждой БППС. Сравнив расположения точки № 5, которая соответствует БППС № 5, на диаграммах, можно заметить, что в работе БППС №5 наблюдается улучшение.

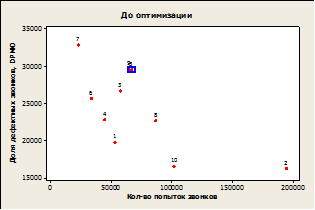
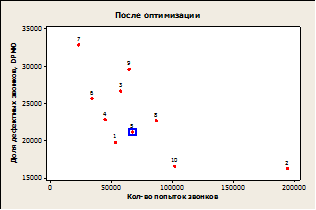
Рисунок 1. Диаграммы рассеяния доли дефектных звонков и количества попыток звонков каждой БППС до оптимизации (слева) и после оптимизации (справа)

Выводы. Описанный в п.III алгоритм возможно использовать для поддержки принятия решения по выбору БППС с целью проведения в них оптимизационных работ и автоматического выявления выбросов в связке доли дефектных звонков и количества попыток звонков каждой БППС.

Список литературы:

1.Зингеренко Ю.А. Основы построения телекоммуникационных систем и сетей / Конспект лекций. СПб: СПбГУ ИТМО, 2005. — 143 с. [Электронный ресурс] — Режим доступа. — URL: http://books.ifmo.ru/file/pdf/85.pdf (дата обращения: 14.11.2014).

2.Наимов А.Н., Хакимов Р.И. Математические вопросы эффективного обслуживания телефонных звонков абонентов сотовой связи // Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2014). Сборник трудов VII международной конференции (Воронеж, 14—21 сентября 2014 г.) Воронеж: Издательство «Научная книга» 2014. — С. 270—275.

3.Обзор системы GSM. Корпоративный тренинг. - Вымпелком, 2004. [Электронный ресурс] — Режим доступа. — URL: http://www.radioscanner.ru/files/download/file2460/obzor_sistemy_gsm.rar (дата обращения: 11.11.2014).

4.Ericsson WCDMA System Overview. LZT 123 6208 R5B © Ericsson, 2006.

5.Jui-Chi Chen et al. Utilization Optimization for OVSF Multi-code Assignment in WCDMA Networks/ Asian Journal of Health and Information Sciences, — Vol. 2, — № 1—4, — pp. 49—65, — 2007.

6.Martin KOLLÁR. EVALUATION OF REAL CALL SET UP SUCCESS RATE IN GSM. Acta Electrotechnica et Informatica — Vol. 8, — № 3, — 2008, — pp. 53—56, ISSN 1335-8243 © 2008 FEI TUKE

7.Mudassar Ali, Asim Shehzad, Dr. M.Adeel Akram. Radio Access Network Audit & Optimization in GSM (Radio Access Network Quality Improvement Techniques). International Journal of Engineering & Technology IJET-IJENS Vol. 10 — № 01, 108401-2727 IJET-IJENS © February 2010 IJENS.

8.Pierre Zune. Family of RBS 3000 products for WCDMA systems Ericsson Review № 3, 2000.