КООПЕРАТИВНЫЕ  ДИФФЕРЕНЦИАЛЬНЫЕ  ИГРЫ  С  ОГРАНИЧЕННГЫМИ  РЕСУРСАМИ  У  ИГРОКОВ

Скитович  Владимир  Викторович

доцент,  канд.  физ.-мат.  наук,  Санкт-Петербургский  государственный  университет,  РФ,  г.  Санкт- Петербург

Email: 

COOPERATIVE   DIFFERENTIAL  GAMES  WITH  LIMITED  RESOURCES  AT  PLAYERS

Vladimir  Skitovich

associate  Professor,  candidate  of  physical-mathematical  Sciences,  St.  Petersburg  state  University,  Russia,  St.  Petersburg

АННОТАЦИЯ

В  статье  рассматривается  проблема  устойчивости  коллективных  соглашений  в  кооперативных  дифференциальных  играх.  Построены  побочные  платежи,  которые  обеспечивают  для  достигнутого  игроками  соглашения  устойчивость  по  Нэшу.  Найдены  достаточные  условия,  при  которых  рассмотренное  коллективное  соглашение  будет  устойчивым. 

ABSTRACT

The  article  deals  with  the  problem  of  stability  of  collective  agreements  in  cooperative  differential  games.  Built  side  payments  which  provide  for  the  agreement  reached  by  players  Nash  equilibrium.  Found  sufficient  conditions  under  which  reviewed  the  collective  agreement  will  be  sustainable.

Ключевые  слова :  кооперативные  игры;  дележ;  побочные  платежи;  устой­чивость;  коллективные  соглашения.

Keywords :  cooperative  games;  payoff  vector;  side  payments;  stability;  collective  agreements

Дадим  формальное  определение  рассматриваемого  класса  игр  n  лиц.  Пусть  динамика  развития  игры  задается  дифференциальным  уравнением: 

  с  начальным  условием  ,  (1) 

где:      —  управления  выбираемые  игроками; 

T   —  момент  времени  окончания  игры.

Если  в  результате  выбранных  игроками  управлений  реализуется  траекто­рия  ,  ,  то  степень  удовлетворения  интересов  каждого  из  игроков  определяется  его  функцией  выигрыша:

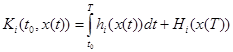  ,  (2) 

где:    —  текущий  выигрыш  i-ого  игрока  к  моменту  времени  t  ; 

  —  терминальный  выигрыш,  получаемый  отдельным  игроком  в  момент  окончания  игры. 

Кооперативный  характер  игры  предполагает  трансферабельность  выигрышей  и  возможность  совместных  действий  игроков,  т.  е.  образование  коалиций  ,  где  N  —  множество  всех  участников  игры  .  Потенциальные  возможности  отдельной  коалиции  S  определяются  характеристической  функцией  игры  —  ,  которая  в  данном  случае  будет  иметь  следующий  вид:

  .  (3) 

При  этом,  характеристическая  функция  общей  коалиции  будет  равна

  ,  (4) 

где    —  оптимальная  траектория  данной  игры,  вдоль  которой  суммар­ный  выигрыш  игроков  максимален.

Поскольку  реализация  оптимальной  траектории  игры  требует  согласован­ных  действий  всех  игроков,  а  интересы  каждого  из  них  будут  удовлетворены  в  различной  степени,  то  необходимым  условием  общего  согласия  становится  распределение  индивидуальных  доходов.  Поэтому  под  решением  кооператив­ной  игры  понимается  некоторый  дележ  ,  удовлетворяющий  следующим  условиям:

1.  Условие  индивидуальной  рациональности  :  ,  .

2.  Условие  коллективной  рациональности  :  .

Выбор  дележа  представляет  собой  самостоятельную  проблему,  которой  за­нимаются  и  социологи,  и  политологи,  и  математики.  Поэтому  будем  считать,  что  дележ  d  однозначно  определяется  некоторым  принципом  оптимальности,  признаваемым  всеми  игроками  и  реализующим  господствующее  понимание  со­циальной  справедливости.  Сформулированную  таким  образом  дифференциаль­ную  игру  обозначим  через  .

Реализация  дележа  достигается  путем  выплаты  игроками  в  ходе  игры  по­бочных  платежей.  Под  побочными  платежами  в  игре    будем  понимать  вектор-функцию  ,  которая  обладает  следующими  свойствами:

1. 

2. 

3. 

где    —  размер  выплат  отдельному  игроку  остальными  игроками  к  мо­менту  времени  (или  наоборот,  если  значение  функции    оказывает­ся  отрицательным). 

Предполагается,  что  для  осуществления  побочных  платежей  каждый  из  игроков  обладает  определенным  количеством  ,  некоторого  трансферабельного  ресурса,  а  также  может  использовать  текущий  выигрыш.  Побочные  платежи    будем  называть  реализуемыми,  если  игроки  в  состоянии  их  осуществить,  т.  е.  для  всех  значений    выполняются  неравенства:

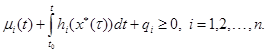  (5)

Таким  образом,  коллективное  соглашение  в  игре    будет  собой  пред­ставлять  тройку  ,  где    —  оптимальная  траектория  развития  игры,  d  —  дележ,    —  побочные  платежи,  реализующие  этот  дележ. 

Для  анализа  устойчивости  возможных  соглашений,  наряду  с  игрой    будем  рассматривать  также  порождаемые  ею  подыгры  ,  которые  отли­чаются  от  исходной  игры  только  начальными  условиями  и  продолжительно­стью.  Характеристическую  функцию  и  дележ  в  подыгре    обозначим  соответственно  через    и  d(t),  значения  которых  определяются  по  тем  же  правилам,  что  и  в  исходной  игре.  При  этом  значения  характеристических  функций  игры  и  подыгр  будут  связаны  между  собой  сле­дующими  уравнениями  Беллмана: 

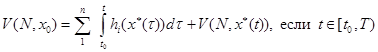    (6)

  (7)

Коллективное  соглашение    будем  называть  устойчивым,  если  для  любой  коалиции    в  каждый  момент  времени    выполняется  неравенство:

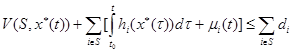.  (8)

Содержательно,  это  определение  означает,  что  ни  одной  из  коалиций  невыгодно  в  ходе  игры  нарушить  достигнутое  соглашение  и  начать  действовать  самостоятельно.  Анализ  неравенств,  определяемых  формулой  (8),  позволяет  сделать  ряд  выводов.  Пусть  ,  тогда  неравенство  (8)  примет  следующий  вид: 

    .  (9)

В  теории  кооперативных  игр  неравенства  (9)  известны  как  условие  коалиционной  рациональности  и  множество  дележей  удовлетворяющих  этому  условию  принято  называть  ядром  игры.  Исходя  из  этого,  можно  сделать  следующий  вывод:

Утверждение  1.  Для  устойчивости  соглашения    необходимо,  чтобы  вектор  дележей  d  принадлежал  ядру  игры  .

Рассмотрим  другой  частный  случай,  когда  функция  побочных  платежей  построена  следующим  образом:

,  .  (10)

Содержательный  смысл  формулы  (10)  состоит  в  том,  что  если  в  какой-либо  момент  времени    соглашение  будет  пересмотрено,  то  в  силу  равенства  (6)  суммарный  выигрыш  игроков  останется  неизменным  и  индивидуальные  выигрыши  также  не  изменятся,  поскольку

,  .  (11)

Следовательно,  на  индивидуальном  уровне  ни  одному  из  игроков  нет  смысла  в  ходе  игры  настаивать  на  пересмотре  соглашения.

Утверждение  2.  Если  побочные  платежи  ,    реализуемы,  то  коллективное  соглашение    будет  равновесным  по  Нэшу.

Однако  не  исключено,  что  нарушение  соглашения  может  в  какой-либо  момент  времени  оказаться  выгодным  для  некоторой  из  коалиций.  Нетрудно  проверить,  что  побочные  платежи  ,    обеспечивают  выполнение  неравенства  (8),  если  для  каждой  из  подыгр    выполняется  условие  коалиционной  рациональности: 

,  .

Утверждение  3.  Если  для  всех  значений    дележ    принадлежит  ядру  подыгры  ,  а  побочные  платежи    реализуемы,  то  коллективное  соглашение    будет  устойчивым.

К  сожалению,  большинство  содержательных  игр  имеет  пустое  ядро  и  поэтому  весьма  часто  коллективные  соглашения  оказываются  неустойчивыми.  Исключение  представляют  игры  двух  лиц,  для  которых  ядро  всегда  не  пусто  и  совпадает  с  множеством  всех  дележей.  В  этом  случае  вопрос  устойчивости  сводится  к  ресурсному  обеспечению  и  отысканию  реализуемых  побочных  платежей.  Полученные  результаты  позволяют  объяснить  популярность  и  эффективность  двусторонних  соглашений,  особенно,  когда  речь  идет  об  обеспечении  безопасности  договаривающихся  сторон.  Для  обеспечения  устойчивости  многосторонних  соглашений  необходимо  создание  и  развитие  соответствующих  социальных  институтов,  таких  как  право,  суд,  армия  и  т.  п.