ВВЕДЕНИЕ  АФФИННЫХ  И  НОРМАЛЬНЫХ  СВЯЗНОСТЕЙ  НА  ГИПЕРПОЛОСЕ 

Попов  Юрий  Иванович

канд.  физ.-мат.  наук,  профессор  Балтийского  федерального  университета

имени  И.  Канта,  РФ,  г.  Калининград,

E-mail: 

 

INTRODUCTION  AFFINITY  AND  NORMAL  CONNECTION  ON  HYPERBANDS 

Popov  Yuri

candidate  of  Science,  professor  of  Baltic  federal  university  of  I.  Kant,  Russia,  Kaliningrad

 

Аннотация

Данная  статья  является  продолжением  работы  [5],  в  которой  рассматривается  геометрия  специального  класса  регулярных  гиперполос    проективного  пространства  .  Вводятся  аффинные  (касательные)  и  нормальные  (центропроективные)  связности  на  гиперполосе.  Найдены  тензоры  кривизны  (кручения)  этих  связностей.  Работа  выполнена  методом  Г.Ф.  Лаптева  [1].  Во  всей  работе  индексы  принимают  значения 

;I,  J,  K,…p,q,s,…=i,  j,  k,…;  a,b,c,…;

  α,β,γ,…;i,j,k,…=(a,p);;

.

ABSTRACT

This  article  is  a  continuation  of  [5],  which  deals  with  the  geometry  of  a  special  class  of  regular  hyperbands  projective  space.  We  introduce  affine  (tangential)  and  normal  (Centroprojective)  connections  on  hyperstrip.  Found  curvature  tensors  (torsion)  of  these  connections.  Work  performed  by  G.F.  Laptev  [1].  Throughout  the  paper  the  indices  take  values  ;I,  J,  K,…p,q,s,…=i,  j,  k,…;  a,b,c,…;

  α,β,γ,…;i,j,k,…=(a,p);;

.

 

Ключевые  слова:   гиперполоса;  афинная  связность;  нормальная  связность.

Keywords:  hyperbands;  affinity  connection;  normal  connection.

 

§   1.  Касательная  и  нормальная  связности  гиперполосы

1.  Следуя  работе  [1]  формулы  инфинитезимального  перемещения  репера  запишем  в  виде

 

  ,    (1) 

 

Так  как  реперы    и    в  проективном  пространстве    отождествляются,  то  для  проективной  группы    существенна  лишь  разница

 

  ,  (2)

 

где    и    одновременно  не  равны  нулю;  очевидно,  что  .

Для  форм    из  (1),  (2)  вытекают  следующие  структурные  уравнения  [2]:

 

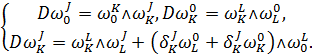  (3)

 

2.     Известно  [5],  что  гиперполоса  ⊂  P_n  задается  уравнениями 

 

  (4)

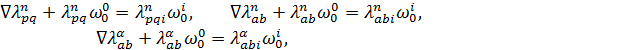
  (5)

 

Пусть  гиперполоса    [5],  заданная  уравнениями  (4),  (5),  оснащена  в  смысле  Нордена  [3],  то  есть  оснащена  полями  нормалей    1-го  рода  и  полями  нормалей    2-го  рода.  Адаптируем  репер    [5]  полям  нормалей  1-го  и  2-го  рода,  т.  е.  точки  ,  ,,.

В  этом  случае  формы  ,  становятся  главными:

 

  ,  ,  ,  ,    (6)

 

где 

 

  ,  ,  , 

  ,   (7)

 

Таким  образом,  уравнения  (4)—(7)  являются  уравнениями  нормализованной  по  Нордену  гиперполосы    в  дифференциальной  окрестности  3-го  порядка.  Кроме  того,  из  (6)  следует,  что

 

  ,    (8)

 

и  из  формул  (4)  и  (6)  находим,  что

 

  ,    (9)

 

где    и    в  силу  сопряженности  плоскостей  Λ  и  L  [5].

Из  задания  гиперполосы  (4)—(7)  следует,  что  при  фиксации  точки    базисной  поверхности    касательные  плоскости    и  нормальные  плоскости  ,    остаются  неподвижными.  Тогда  в  силу  [3],  [6]  на  базе    возникают  нормальные  ,    и  касательные  расслоения    плоскостей.  В  силу  (3),  (6),  (7),  (8),  (9)  структурные  уравнения  касательного  (аффинного)  расслоения    гиперполосы    принимают  вид

 

  ,  ,  (10)

 

где

 

    (11)

    (12)

 

Согласно  теореме  Картана-Лаптева  [7],  [1]  следует,  что  в  касательном  расслоении    гиперполосы  ,  нормализованной  по  Нордену,  определяется  аффинная  связность    без  кручения.  Впервые  эту  связность  ввел  и  подробно  исследовал  А.П.  Норден  [3].  Формы    будут  ее  формами  связности,  а  формы    —  ее  формами  кривизны,  а    —  тензор  кривизны  связности  .

Теорема  1.  В  дифференциальной  окрестности  3-го  порядка  на  нормализованной  по  Нордену  гиперполосе  ⊂  P_n  в  ее  касательном  расслоении  определяется  аффинная  связность    без  кручения  с  2-формами    (11)  кривизны,  тензор  кривизны  которой  имеет  строение  (12).

3.  Структурные  уравнения  нормального  расслоения    (расслоения  нормалей  1-го  рода  гиперполосы)  с  учетом  (3),  (8),  (9)  можно  представить  в  виде:

 

,  ,

=

,

  (13)

 

где 

 

  , 

  ,  ,  (14)

 

 

    ,

  ,  ,  (15)

  ,  .

 

Согласно  работам  [4],  [6],  получаем,  что  в  нормальном  расслоении  возникает  центропроективная  связность    с  формами  связности  и  2-формами    кривизны,  [6]  компоненты  тензора  кривизны  ,  которой  имеют  строение  (15).  Связность    будем  называть  нормальной  проективной  связностью  оснащенной  гиперполосы  .

Таким  образом,  имеет  место 

Теорема  2.   В  дифференциальной  окрестности  3-го  порядка  на  базисной  поверхности    гиперполосы  ⊂  P_n  определяется  нормальная  связность    в  расслоении  ее  нормалей  1-го  рода  .  Компоненты  тензора  кривизны  связности    имеют  строение  (15),  а  2-  формы  кривизны  соответственно  (14).

§  2.  Задание  аффинных  и  нормальных  связностей,  индуцируемых 

-  ,-∆  —  подрасслоениями

1.  Структурные  уравнения  касательного  -подрасслоения  имеют  вид:

 

,  (17)

 

где  совокупность  величин 

 

  (18)

 

образует  тензор  кручения  {},  а  2-формы  кривизны    имеют  структуру:

 

  (19)

 

Следуя  работам  [4],  [6],  утверждаем,  что  в  слоях  касательного  -подрасслоения  индуцируется  аффинная  связность    [3]  с  кручением  {}  (18),  компоненты  тензора  кривизны  {},  которой  имеют  вид: 

 

  (20)

 

В  результате  справедлива 

Теорема  3.   Гиперполоса    в  касательном  Λ-подрасслоении  в  дифференциальной  окрестности  3-го  порядка  индуцирует  внутреннюю  аффинную  связность  с  кручением  (18)  и  с  2-формами  кривизны  {}  (19),  тензор  кривизны  {}  которой  имеет  структуру  (20).

2.  Структурные  уравнения  нормального  расслоения    (расслоение  нормалей  1-го  рода  Λ-подрасслоения)  имеют  вид:

 

 

, 

,

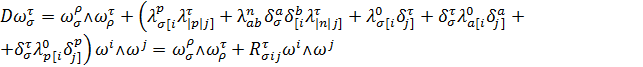,  (21)

, 

, 

, 

 

Где

 

                       (22)

 

2-формы  кривизны,  а  компоненты  тензора  кривизны  {}имеют  строение:

 

,  (23)

 

Резюмируя,  получим  предложение

Теорема  4.  Гиперполоса  в  нормальном  расслоении  N_n-r(V)  (в  расслоении  нормалей  1-го  рода  Λ  —  подрасслоения)в  дифференциальной  окрестности  3-го  порядка  порождает  внутренним  образом  нормальную  связность    со  слоевыми  формами  связности  ()  и  2-формами  кривизны  ()  (22).  Компоненты  тензора  кривизны  {}  имеют  вид  (23).

3.  Структурные  уравнения  касательного  -подрасслоения  представим  таким  образом:

 

                 (24)

 

 

где  компоненты  тензора  кручения 

 

    (25)

 

а  тензор  кривизны  {}  имеет  строение:

 

  (26)

 

Теорема  5.   В  дифференциальной  окрестности  3-го  порядка  в  касательном  -подрасслоения  гиперполосы  ⊂  P_n  индуцируется  аффинная  связность  с  кручением  (25)  и  с  2-формами  кривизны 

= ,  тензор  кривизны  которой  имеет  вид    (26).

4.  Структурные  уравнения  нормального  расслоения    (расслоение  нормалей  1-го  рода  L-подрасслоения)  можно  представить  в  виде:

 

  , 

, 

    (27)

,, 

,

 

где 

 

,  ,

,  (28)

 

являются  2-формами  кривизны,  а  компоненты  тензора  кривизны  имеют  такую  структуру:

 

,  ,

,    (30)

,  .

 

В  результате  справедлива 

Теорема  6.  В  нормальном  расслоении    гиперполоса  порождает  в  дифференциальной  окрестности  3-го  порядка  внутренним  образом  нормальную  связность    со  слоевыми  формами  связности  ( )  и  2-формами  кривизны  ().  Компоненты  тензора  кривизны  имеют  строение  (30).

5.  Структурные  уравнения  нормального    -  подрасслоения  можно  представить  в  виде:

 

 

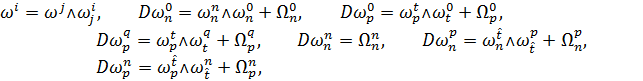
где 

 

  (30)

, 

 

являются  2-формами  кривизны,  а  компоненты  тензора  {  кривизны  имеют  такое  строение:

 

,(31)

 

Таким  образом,  имеет  место

Теорема  7.  В  дифференциальной  окрестности  3-го  порядка  гиперполоса    порождает  внутренним  образом  в  -  подрасслоении  нормальную  связность  ,  2-формы  кривизны  и  компоненты  тензора  кривизны  которой  {  имеют  соответственно  вид  (30)  и  (31).

 

Список  литературы:

1.Лаптев  Г.Ф.  Дифференциальная  геометрия  погруженных  многообразий.  Теоретико-групповой  метод  дифференциальных  геометрических  исследований  //  Тр.  Моск.  мат.  об-ва.  —  1953  —  т.  2.  —  с.  275—382.

2.Лумисте  Ю.Г.  Проективные  связности  в  канонических  расслоениях  многообразий  плоскостей.  Матем.  сб.  —  1973,  91(133),  —  №  2(6),  —  с.  211—233.

3.Норден  А.П.  Пространства  афинной  связности.  М.,  1976.

4.Остиану  Н.М.,  Рыжков  В.В.,  Швейкин  П.И.  Очерк  научных  исследований  Германа  Федоровича  Лаптева.  Труды  Геометрич.  семинара.  ВИНИТИ  АН  СССР,  —  1973,  —  т.  4,  —  с.  7—70.

5.Попов  Ю.И.  Нормализации,  ассоциированные  с  гиперполосой  Нm().  VII  Международная  научно-практическая  конференция  «Современные  концепции  научных  исследований»  (часть  2),  г.  Москва,  30—31  октября  —  2014,  —  №  7,  —  стр.  45—49.

6.Чакмазян  А.В.  Номальная  связность  в  геометрии  подмногообразий,  Монография;  Ереван,  1990.  —  116  с.

7.Cartan  E.  Les  spaces    connexion  projective//Тр.  Семинара  по  векторному  и  тензорному  анализу  /  МГУ.  М.,  —  1937.  —  Вып.  4  —  с.  147—159.