ПОЛЯ  ГЕОМЕТРИЧЕСКИХ  ОБЪЕКТОВ  H   -РАСПРЕДЕЛЕНИЕ  ПРОЕКТИВНОГО  ПРОСТРАНСТВА

Будылкин  Андрей  Александрович

аспирант  Балтийского  федерального  университета  имени  И.  Канта,  РФ,  г.  Калининград

E -mail:  AndreyBudylkin@rambler.ru

 

FIELDS  OF  GEOMETRIC  OBJECTS   H  -DISTIBUTION  OF  PROJECTIVE  SPACE

Budylkin  Andrey

graduate  student  of  Baltic  federal  university  of  I.  Kant ,  Russia,  Kaliningrad

 

АННОТАЦИЯ

Дано  задание  H-распределения  в  P_n  [7].  Рассмотрены  поля  геометрических  объектов  в  дифференциальной  окрестности  1-го  порядка  [3],  [4].  Построены  нормализации  в  смысле  Нордена  [5]  и  квазинормали  [6]  основных  структурных  подрасслоений  H-распределения,  в  дифференциальной  окрестности  1-го,  2-го  порядка.  Изучение  H-распределений  актуально,  так  как  эти  образы  являются  обобщениями  специальных  классов  регулярных  гиперполос  [2]  [8],  гиперповерхностей  и  гиперполосных  распределений[9].  Работа  выполнена  методом  Лаптева  Г.Ф.  [3]  Индексы:

;I,  J,  K,…σ,ρ,τ,…=i,  j,  k,…;  α,β,γ,….

ABSTRACT

Given  a  presentation  of  H-distribution  of  Pn  [7].  Considered  fields  of  geometric  objects  in  the  differential  neighborhood  of  the  1st  order  [3],  [4].  Built  normalizations[5]  in  the  sense  of  Norden  and  kvazinormali[6]  of  the  main  structural  subbundles,  in  the  differential  neighborhood  of  the  1st,  2nd  order.  Study  of  H-distributions  is  important,  because  these  images  are  generalizations  of  the  special  classes  of  regular  hyperbands  [2]  and  hyperband  distribution  [9].  Work  performed  by  G.F.  Laptev  [3]  Indices: 

;I,  J,  K,…σ,ρ,τ,…=i,  j,  k,…;  α,β,γ,….

 

Ключевые  слова:   распределение;  тензор;  квазитензор;  нормализация;  квазинормаль;  геометрический  объект.

Keywords:  distribution;  tensor;  kvazitensor;  normalization;  quasinormal;  geometric  object.

 

§  1.  Задание  H-распределения  в  n-мерном  проективном  пространстве

Определение.   Скомпонованным  гиперплоскостным  распределением  (H-распределением)  [7]  называется  гиперплоскостное  Н-распределение,  в  каждом  центре  Х  которого  зафиксированы  две  плоскости  Λ_m(Х),  L_n-m-1(Х)  такие,  что  выполняются  соотношения: 

 

[Λ_m(Х),  L_n-m-1(Х)]=H_n-1(Х),  Λ_m(Х)∩  L_n-m-1(Х)=Х  .

 

Присоединим  к  образующему  элементу  H-распределения  проективный  репер  R₀={A₀,  A_I}  следующим  образом:  Х≡A₀,{А_i}Λ(A₀),  А_α    L(A₀),  А_n    Н_n-1. 

В  репере  R₀  H-распределение  задается  следующим  образом:

 

  (1)

 

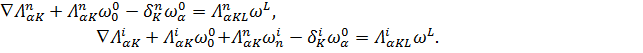
Функции,  стоящие  в  правых  частях  равенств,  вообще  говоря,  являются  несимметричными  по  нижним  индексам.

Совокупности  функций  Г₁=,  Г₂=  образуют  фундаментальные  объекты  [2]  1-го  и  2-го  порядка  H-распределения.  Продолжения  уравнений  (1)  вводят  в  рассмотрение  фундаментальные  объекты  более  высоких  порядков  Г₁ÌГ₂ÌГ₃ÌГ₄Ì.  Имеет  место  теорема  существования  H-распределения  [1]:

Теорема  1.  В  n-мерном  проективном  пространстве  в  репере  R₀  гиперплоскостное  скомпонованное  распределение  задается  с  произволом  (2m+1)(n-m-1)+m  функций  от  n  аргументов.

§  2.  Построение  полей  геометрических  объектов  H-распределения  в  дифференциальной  окрестности  первого  порядка

В  дальнейшем  будем  рассматривать  H-распределение,  для  которого  в  каждом  центре  А₀  плоскость  L_n-m-1  сопряжена  с  плоскостью  Λ_m  относительно  главного  фундаментального  тензора,  т.е.  выполняются  условия

 

    (2)

 

В  этом  случае  компоненты  тензора  будут  иметь  следующее  строение:

 

 

Мы  рассматриваем  регулярное  H-распределение  [8],  для  которого  тензор  невырожденный,  т.е.    (3)

Следовательно,  в  силу  (3)  для  тензора  первого  порядка  введём  обращённый  ему  тензор    [3],  удовлетворяющий  следующим  соотношениям  и  уравнениям:

 

 

Аналогично,  для  соответствующих  главных  фундаментальных  тензоров  -  ,L-,  подрасслоений  вводим  обращённые  им  соответствующие  тензоры  ,  такие,  что 

 

 

Следуя  работе  Остиану  Н.М.  [6]  вводим  соответсвия  Бомпьяни-Пантази  между  нормалями  1-го  и  2-го  рода  соответсвенно  Н-,Λ-,  L-  подрасслоений:

 

 

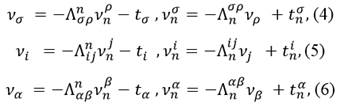
где 

 

 

С  учетом  условий  (2)  уравнения  (1)  примут  вид:

 

  (7)

   

 

Введём  нормализацию  в  смысле  Нордена  [5]  для  Λ-подрасслоения.

Определение.   Λ-подрасслоение  назовем  нормализованным  в  смысле  Нордена,  если  к  нему  инвариантным  образом  присоединены  поля  нормалей  первого  рода  N_n-m  и  нормалей  второго  рода  N  _m-1  :

 

  (а)    (b)  (8)

 

причём  в  каждом  центре  А₀  нормаль  первого  рода  N_n-m=[A₀,  A_α,X_n]  проходит  через  плоскость  L_n-m-1ÌH(A₀).

Условие  инвариантности  нормали  N_n-m,  где,  приводит  к  соотношению  (8а).  Если  потребовать,  чтобы  прямая  h=[A₀,X_n]  была  инвариантной,  то  кроме  (8а)  получим  условие 

 

    (9)

 

Уравнения  (9)  выполняются,  если  охват  объекта  {}  осуществить  с  помощью  квазитензора  :  .  В  дальнейшем  считаем,  что  прямая  h=[A₀,X_n],  где  ,  инвариантна.  Нормаль  второго  рода  N_m-1  плоскости  Λ(А₀)  задаётся  точками  ,  где  функции  удовлетворяют  уравнениям  (8b).  Если  охваты  квазитензоров  осуществить  по  формулам 

 

 

где 

то  к  Λ-подрасслоению  в  дифференциальной  окрестности  первого  порядка  внутренним  образом  присоединяется  нормализация  в  смысле  Нордена  .

Рассмотрим  функции  ,  удовлетворяющие  уравнениям 

  Эти  уравнения  определяют  поле  нормалей  второго  рода  для  L-подрасслоения.  В  силу  биекции  (5)  полю  нормалей  второго  рода  соответствует  поле  нормалей  первого  рода  L-подрасслоения  в  дифференциальной  окрестности  первого  порядка:

 

 

Введём  нормализацию  в  смысле  Нордена  [5]  для  L-подрасслоения.

Определение.   L-подрасслоение  назовем  нормализованным  в  смысле  Нордена  [5],  если  к  нему  инвариантным  образом  присоединены  поля  нормалей  первого  рода  N_m+1  и  нормалей  второго  рода  N_n-m-2  :

 

_,

 

причём  в  каждом  центре  А₀  нормаль  первого  рода  N_m+1=[A₀,  A_i,X_n]  проходит  через  плоскость  Λ_mÌH(A₀). 

В  силу  биекции  (6)  полю  нормалей  1-го  рода  {}()  соответствует  поле  нормалей  2-го  рода  L-подрасслоения: 

 

.

 

Функции    удовлетворяют  уравнениям

 

.  (*)

 

Следовательно,  квазитензор  {}  в  каждом  центре  А₀  определяет  нормаль  второго  рода  для  L-подрасслоения.  В  силу  биекции  (6)  полю  нормалей  2-го  рода  (*)  соответствует  поле  нормалей  1-го  рода  L-подрасслоения  в  дифференциальной  окрестности  первого  порядка:

 

 

Теорема  2.   В  дифференциальной  окрестности  первого  порядка  H-распределение  внутренним  образом  порождает  нормализации  L-подрасслоения  и  нормализации  (),  (),  L-подрасслоения  в  смысле  Нордена.

Квазитензоры  функционально  независимы,  поэтому  они  определяют  пучок  нормалей  первого  рода  Λ-подрасслоения  и  по  биекции  (5)  пучок  нормалей  2-го  рода:

 

  ,  .  (10)

 

Аналогично,  для  L-  подрасслоения  получим  пучок  нормалей  1-го  рода  и  по  биекции  (6)  получим  пучок  нормалей  2-го  рода 

 

  ,  (11) 

 

Совокупности  функций  ,  определяют  поля  нормалей  1-го  рода  Н-подрасслоения:

 

  (12)

 

Поля  (12)  в  силу  биекции  (4)  порождают  поля  нормалей  второго  рода  Н-подрасслоения:

 

    (13)

 

Построенные  поля  (13)  порождают  пучки  нормалей  1-го  и  2-го  рода  Н-подрасслоения:

 

  ,  .  (14)

 

Теорема  3.   В  дифференциальной  окрестности  первого  порядка  H-распределение  внутренним  образом  порождает  в  каждом  центре  А₀  пучки  нормалей  1-го  и  2-го  рода  (10),  (11),  (14)  соответственно  Λ-,  L-,  Н-подрасслоений.

§  3.  Квазитензоры  и  квазинормали   H-распределения  в  дифференциальной  окрестности  первого  порядка

Согласно  [4],  систему  величин    назовём  квазинормалью  H-распределения,  если  при  преобразованиях  стационарной  подгруппы  элемента  распределения  имеем  один  из  следующих  законов  преобразования  :

 

 

  (15)

 

 

где  l,  µ  —  постоянные  числа,  не  равные  нулю.

I .  Квазинормали  и  нормали,  ассоциированные  с  L-подрасслоением

Учитывая  уравнения  (7),(*),  построим  следующие  квазинормали  в  дифференциальной  окрестности  первого  порядка.

 

  (16)

 

Один  из  способов  получения  инвариантных  нормалей  ,    1-го  и  2-го  родов  H-распределения  заключается  в  нахождении  общих  нормалей  (в  общем  случае  единственных)  двух  квазинормалей.  Например,  для  L-подрасслоения  имеем  следующие  построения  в  дифференциальной  окрестности  первого  порядка.  Пара    определяет  инвариантные  нормали

 

 

В  дальнейшем  это  соответствие  будем  обозначать  следующим  образом: 

а.   ,

б.  ,

в.   , 

г.   , 

д.  , 

е.   . 

Теорема  4.   В  дифференциальной  окрестности  1-го  порядка  H-распределение  внутренним  инвариантным  образом  порождает  шесть  нормализаций    L-под-расслоения.

II .  Нормализации,  ассоциированные  с  L-подрасслоением  H-распределения

В  силу  уравнений  (7)  получаем  следующие  дифференциальные  уравнения  квазинормалей  L-подрасслоения  в  дифференциальной  окрестности  1-го  порядка:

 

(17)

 

Квазинормали  (17)  порождают  следующие  пары  нормалей  1-го  и  2-го  рода  L-подрасслоения  в  дифференциальной  окрестности  1-го  порядка:

а.  

б. 

в.    

г.   ,

д.   

е.    

Итак,  справедлива

Теорема  5.   В  дифференциальной  окрестности  1-го  порядка  H-распределение  внутренним  инвариантным  образом  порождает  шесть  нормализаций    L-подрасслоения.

§  4.  Построение  квазинормалей  и  нормалей   основных  структурных  подрасслоений  в  дифференциальной  окрестности  второго  порядка

I .  Так  как  L-подрасслоение  невырождено,  тогда 

 

    (18)

 

Дифференцируя  (18),  получим 

 

  ,  (19)

 

где  . 

Продолжение  уравнения  (19)  с  учетом  (7)  приводит  к  уравнениям

 

.  (20)

 

Отсюда  при  K=i,  в  частности,  получаем  уравнение 

 

,

 

которое  при  фиксации  центра  А₀  H-распределения  примет  вид

 

    (21)

 

Таким  образом,  совокупность  функций 

 

, 

 

определяет  в  дифференциальной  окрестности  второго  порядка  квазинормаль,  ассоциированную  с  L-подрасслоением.  Полагая  К=,  из  (20)  получаем

 

  .  (22)

 

Введём  в  рассмотрение  функции 

 

  (23)

 

которые  в  силу  (22)  при  фиксации  центра  А₀  H-распределения  удовлетворяет  уравненям

 

    .  (24)

 

Из  (24)  следует,  что  совокупность  функций    есть  квазинормаль  2-го  порядка  L-подрасслоения.

II .  Аналогично  п.1,  учитывая,  что  L-подрасслоение  невырождено,  т.  е.

 

  ,  (25) 

 

и  дифференцируя  (25),  получим 

 

,  (26)

 

где    . 

Продолжая  уравнения  (26)  с  учетом  (7),  получим

 

.  (27)

 

Из  (27)  при  К=i,  К=α  находим

 

,  (28)

.  (29)

 

Функции

 

,    (30)

 

при  фиксации  точки  А  (центра  H  -распределения)  в  силу  соответственно  (28),(29)  удовлетворяют  уравнениям 

 

  ,  (31)

  .  (32)

 

Согласно  определению  (15)  из  (31),(32)  следует,  что  совокупности  функций  {},{}  образуют  квазинормали  в  дифференциальной  окрестности  2-го  порядка,  ассоциированные  соответственно  с  Λ-  и  L-  подрасслоениями.

III .  Используя  квазинормали  (17)  и  (21),  (31),  вводим  нормализации  Λ-  подрасслоения,  при  условии,  что  тензор  неголономности 

равен 

 

   

    (33)

 

С  помощью  квазинормалей  (17),(21),(28)  находим  в  дифференциальной  окрестности  2-го  порядка  поля  нормалей  2-го  рода  внутренним  образом  присоединенных  к  L-подрасслоению:

 

  (34)

 

Функции  (34)  удовлетворяют  уравнению  типа    .

По  биекции  Бомпьяни-Пантази  (5)  для  нормалей  (34)  2-го  рода  получаем  соответственно  нормали  1-го  рода  Λ  —  подрасслоения:

 

 

Теорема  6.   H-распределение  в  дифференциальной  окрестности  2-го  порядка  внутренним  образом  порождает  два  поля  нормализаций    L-подрасслоения,  если  тензор  неголономности  равен  нулю  т.е.    и  шесть  полей  нормализаций  в  смысле  Нордена  ,  если 

IV .  Если  тензор  неголономности  L-подрасслоения    равен  ,  то  можно,  используя  квазинормали  ,  ,  ,  построить  нормализации  ,  L-подрасслоения  в  дифференциальной  окрестности  2-го  порядка:

 

 

Если  тензор  неголономности  L-подрасслоения    то  нормалям  2-го  рода

 

  (35)

 

в  биекции  Бомпьяни-Пантази  (6),  соответствуют  нормали  1-го  рода  L-подрасслоения  в  дифференциальной  окрестности  2-го  порядка:

 

 

Функции  (35)  удовлетворяют  уравнению  типа    .

Теорема  7.   В  дифференциальной  окрестности  2-го  порядка  H-распределение  внутренним  образом  порождает  две  нормализации  L-подрасслоения    если  тензор  неголономности  L-подрасслоения  равен  нулю,  и  шесть  нормализаций  в  смысле  Нордена  ,  если 

 

Список  литературы:

1.Будылкин  А.А.  Естественные  и  математические  науки  в  современном  мире.  г.  Новосибирск,  —  2015,  —  №  2(26),  —  с.  24—33.

2.Вагнер  В.В.  Теория  поля  локальных  гиперполос.  Тр.  Семинара  по  векторному  и  тензорному  анализу  —  1950.  —  Вып.  8.  —  С.  197—272.

3.Лаптев  Г.Ф.  Дифференциальная  геометрия  погруженных  многообразий.  Теоретико-групповой  метод  дифференциально-геометрических  исследований.  Тр.  Моск.  мат.  об-ва.  —  1953.  —  Т.  2.  —  С.  275—382.

4.Лаптев  Г.Ф.,  Остиану  Н.М.  Распределения  m-мерных  линейных  элементов  в  пространстве  проективной  связности.  Тр.  Геометрического  семинара.  ВИНИТИ.  —  1971,  —  Т.  3,  —  с.  49—94.

5.Норден  А.П.  Пространства  аффинной  связности.  М.:  Наука,  1976.  —  432  с.

6.Остиану  Н.М.  Распределение  гиперплоскостных  элементов  в  проективном  пространстве.  Тр.  Геометрического  семинара.  ВИНИТИ.  —  1973,  —  Т.  4,  —  с.  7—70.

7.Попов  Ю.И.  Основы  теории  трехсоставных  распределений  проективного  пространства.  Монография.  Санкт-Петербург.  Из-во  С-Петербургского  университета,  1972.  —  172  с. 

8.Попов  Ю.В.,  Столяров  А.В.  Специальные  классы  регулярных  гиперполос  проективного  пространства.  К-д,  2011.  Учебное  пособие,  из-е  2-ое,  БФУ  им.  Иммануила  Канта,  —  122  стр.

9.Cтоляров  А.В.  Проективно-дифференциальная  геометрия  регулярного  гиперполосного  распределения  m-мерных  линейных  элементов.  В  кн.:  Проблемы  геометрии  (Итоги  науки  и  техн.  ВИНИТИ  АН  СССР),  М.,  —  1975,  —  Т.  7,  —  с.  117—151.