ТРЕУГОЛЬНЫЕ  И  ПИРАМИДАЛЬНЫЕ  УРАВНЕНИЯ

Мамедяров  Даглар  Мамедярович

канд.  пед.  наук  Дербентский  филиал  «Московский  государственный  гуманитарный  университет  им.  М. А.  Шолохова»,  РФ,  г.  Дербент

E-mail: 

 

TRIANGLE  AND  PYRAMIDAL  EQUATIONS

Daglar  Mamedyarov

candidate  of  Pedagogic  Sciences,  Derbent  branch  of  Sholokhov  Moscow  State  University  for  the  Humanities,  Russia,  Derbent

 

АННОТАЦИЯ

Данная  статья  посвящена  решению  уравнений,  где  в  роли  переменных  выступают  треугольные  и  пирамидальные  числа.

При  решении  этих  уравнений  используются  различные  свойства  треугольных  и  пирамидальных  чисел,  знакомство  с  которыми  будет  полезно  любителям  математики.

ABSTRACT

  The  article  is  devoted  to  the  solution  of  equations  where  triangle  and  pyramidal  numbers  act  as  variables.  In  solving  these  equations  different  properties  of  triangle  and  pyramidal  numbers  are  used;  it  will  be  useful  for  math  lovers  to  get  to  know  them. 

 

Ключевые  слова:  треугольные  и  пирамидальные  уравнения.

Keywords:  triangle  and  pyramidal  equations. 

 

Из  курса  математики  все  знают,  что  есть  алгебраические,  иррациональные,  тригонометрические,  логарифмические,  показательные  и  другие  комбинированные  виды  уравнений.  Но  никто  и  никогда  не  говорил,  что  есть  треугольные,  пирамидальные  или  треугольно-пирамидальные  уравнения.  В  рассматриваемых  уравнениях  некоторые  переменные  являются  треугольными  и  пирамидальными  числами.  Поэтому  взял  на  себя  смелость  называть  их  так.  Эти  уравнения  являются  неопределенными,  то  есть  имеют  два  и  более  переменных.  Решения  отыскиваются  на  множестве  натуральных  чисел,  но  иногда  в  решение  может  входить  число  0.  Вид  этих  уравнений  выглядит  интригующим.  Поэтому  истинный  любитель  математики  с  удовольствием  и  интересом  возьмется  за  их  решение.

Рассмотрим  несколько  уравнений.

1.  Рассмотрим  в  общем  виде  уравнение  . 

Для  решения  воспользуемся  равенствами:

 

  (1)  и    (2). 

 

Эти  равенства  можно  доказать,  используя  определение  числа  сочетаний.  Перемножая  (1)  и  (2)  получаем: 

 

  (3). 

 

Обозначив  ,  ,  ,  ,  ,  ,  ,  получаем  уравнение  ,  где  . 

Решим  несколько  частных  уравнений. 

1.1.             . 

Решение.  Имеем:  .  Тогда  .  , 

=. 

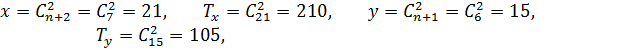
Проверка:  .

Ответ:  . 

1.2.             . 

Решение.  Имеем:  .  Тогда  .  , 

=

.

Проверка:  .

Ответ:  . 

1.3.             . 

Решение.  Имеем:  ,  .  , 

=. 

Проверка:  .

Ответ:  . 

2.  Уравнение  вида  .

Для  решения  воспользуемся  равенством    (4)  или

  .  Введя  обозначения  , 

  получаем  уравнение  . 

В  общем  виде  это  уравнение  имеет  бесконечное  множество  решений.

Рассмотрим  решение  частных  уравнений.

2.1.             .

.  Имеем:  .  Тогда   

,  . 

Проверка:  :  .

Ответ:  .

2.2.             .

.  Имеем:  .  Тогда   

,  . 

Проверка:  .

Ответ:  .

2.3.             .

.  Имеем:  .  Тогда   

,  . 

Проверка:  .

Ответ:  .

3.  Уравнение  вида  .

Воспользуемся  тождеством    или

  .  Введя  обозначения  , 

  получаем  уравнение  . 

В  общем  виде  это  уравнение  имеет  бесконечное  множество  решений.

Рассмотрим  частные  случаи.

3.1.             .

Имеем:  .  Тогда   

,  . 

Проверка:  .

Ответ:  .

3.2.             .

Имеем:  .  Тогда   

,  . 

Проверка:  .

Ответ:  .

3.3.             .

Имеем:  .  Тогда   

,  . 

Проверка:  .

Ответ:  .

4.  Уравнение  вида 

Из  решений  вышеуказанных  уравнений  ясно,  что  любой  куб  можно  представить  в  виде  . 

Так  как  .  Обозначив    имеем  уравнения 

  где 

Уравнения  в  общем  виде  имеют  бесконечное  множество  решений.

Рассмотрим  несколько  частных  уравнений.

4.1.             .

Решение.  Имеем: 

.

Проверка:  .

Ответ:  .

4.2.             .

Решение.  Имеем: 

. 

Проверка:  .

Ответ:  .

4.3.             .

Решение.  Имеем: 

. 

Проверка:  .

Ответ:  .

4.4.             .

Решение.  Имеем: 

. 

Проверка:  .

Ответ:  .

4.5.             .

Решение.  Имеем: 

. 

Проверка:  .

Ответ:  .

4.6.             .

Решение.  Имеем: 

. 

Проверка:  .

Ответ:  .

5.  Рассмотрим  еще  два  вида  уравнений.

а)    б)  .

Для  решения  этих  уравнений  воспользуемся  равенствами 

  и  .  [2.  c.  259]. 

Так  как  эти  равенства  верны  для  любого  ,  где  ,  то  в  общем  виде  уравнения  имеют  бесконечное  множество  решений.  Обозначив    получаем  уравнения  ,  .

Рассмотрим  несколько  частных  уравнений.

5.1.             .

Имеем:  .  Тогда 

.

Проверка:  .

Ответ:  ,  .

5.2.             .

Имеем:  .  Тогда 

.

Проверка:  .

Ответ:  ,  .

5.3.             .

Имеем:  ,  тогда 

.

Проверка:  .

Ответ:  ,  .

5.4.             .

Решение.  Имеем:  ,    тогда 

.

Проверка:  .

Ответ:  ,  . 

5.5.             .

Решение.  Имеем:    тогда  .

Проверка:  .

Ответ:  ,  . 

5.6.             .

Решение.  Имеем:    тогда  .

Проверка:  .

Ответ:  ,  . 

6.  Решение  уравнения  вида  . 

Из  равенства  ,  пользуясь  определением  числа  сочетаний,  получаем 

.  Прибавив  к  обеим  частям  число  3,  получаем 

=.  Отсюда  . 

Введя  новые  обозначения  ,  получаем  уравнение  .

Ясно,  что  уравнение  имеет  бесконечное  множество  решений.  Покажем  одно  из  решений.

Пусть  .  Тогда 

Проверка:  10+8.

7.  Решение  уравнений  вида 

Используя  равенство    [1,  c.  73],  представим

  .  Подставив  это  в  равенство    получаем 

.  Введя  новые  обозначения  ,  получаем  уравнение  .  В  общем  виде  уравнение  имеет  бесконечное  множество  решений.

Решим  несколько  уравнений  частного  вида:

7.1.             Решим  уравнение 

Решение.  Имеем:  тогда 

 

Проверка: 

7.2.             Решим  уравнение 

Решение.  Имеем:  тогда 

 

Проверка: 

7.3.             Решим  уравнение 

Решение.  Имеем:  тогда 

 

Проверка: 

8.  Решение  уравнений  вида  . 

Пользуясь  определением  числа  сочетаний,  из  выражения    получаем  Отсюда    Введя  обозначения 

=,  ,  получаем  уравнение 

 

.

 

Ясно,  что  уравнение  имеет  бесконечное  множество  решений.  Покажем  одно  из  решений.

Приведем  несколько  частных  решений.

Пусть    тогда 

. 

Проверка:  .

Пусть    тогда  . 

Проверка:  .

9.  Решение  уравнений  вида  ,  где  . 

Воспользуемся  равенством    [3,  c.  36].

Обозначив  ,  получаем  уравнение 

Покажем  несколько  уравнений. 

9.1.             .

Решение.  Имеем:  .  Представим  5  в  виде  произведения  .  Это:    или  .

а)  Если    то    Тогда  , 

.

Проверка:  .

б)  Если    то    Тогда  , 

.

Проверка:  .

9.2.             .

Решение.  Представим  12  в  виде  произведения  двух  множителей.  Это:  ;

 

Рассмотрим  каждый  случай.

1.  Тогда

.

Проверка:  .

2.  Тогда 

.

Проверка:  .

3.  тогда 

.

Проверка:  .

4.   

.

Проверка:  .

5.   

.

Проверка:  .

6.   

.

Проверка:  .

Из  решений  этих  уравнений  видно,  что  уравнение  имеет  ровно  столько  решений,  сколько  раз  число    представимо  в  виде  произведения  двух  множителей.

Теперь  решим  несколько  частных  уравнений.

9.3.             .

Пусть  .  Тогда  имеем  уравнение  .

Значит   

Проверка: 

Пусть    тогда  имеем  .  Тогда 

 

Проверка: 

9.4.             .

Решение.  При  .  Имеем  .  Тогда 

 

Проверка: 

При    имеем  уравнение  .  Тогда 

 

Проверка: 

Примечание:  вопрос  о  единственности  решений  этих  уравнений  остается  открытым.

 

Список  литературы:

1.Мамедяров  Д.М.,  Вакилов  Ш.М.  Некоторые  свойства  соединений  и  фигурных  чисел  и  их  применение  при  решении  задач:  Дербент,  2013.  —  228  с. 

2.Мамедяров  Д.М.  Неопределенные  уравнения  и  их  системы:  Дербент,  2013.  —  261  с.

3.Мамедяров  Д.М.,  Вакилов  Ш.М.  Составление  задач  как  способ  развития  творческого  мышления  //  Всероссийская  научно-практическая  конференция.  Материалы  конференции  19—21  сентября:  Махачкала,  2008  —  228  с.