Статья опубликована в рамках: XXI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 августа 2014 г.)
Наука: Математика
Секция: Математическая физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ВЫРОЖДЕННОЕ СОЛИТОННОЕ РЕШЕНИЕ УРАВНЕНИЯ КОРТЕВЕГА-ДЕ ФРИЗА
Хусаинова Галина Владимировна
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E -mail: aldisa@mail.ru
Хусаинов Дамир Зиннурович
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E-mail:
DEGENARATE SOLITON SOLUTION OF KORTEVEG-DE VRIES EQUATION
Khusainova Galina
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
Khusainov Damir
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
АННОТАЦИЯ
Построено точное вырожденное солитонное решение для уравнения Кортевега-де Фриза как предельный (резонансный) случай двухсолитоного решения. Проведён анализ движения сингулярной точки полученного решения.
ABSTRACT
The exact degenerate soliton solution of Korteweg-de Vries equation is constructed as limit (resonance) case of two-soliton solution. Analysis has been done of singularity dynamic of the obtained solution.
Ключевые слова: точное решение; солитон; сингулярность.
Keywords: exact solution; soliton; singularity.
Уравнение Кортевега-де Фриза (КдФ) возникает как реалистическая модель, описывающая движение волн в такой среде, где оказываются существенными слабые нелинейные эффекты [2, c. 19]:
![]() . (1)
. (1)
Известно, что для данного уравнения были построены [6, с. 1192] в явном виде солитонные решения, представляемые в виде стандартных конечных рядов экспонент, где каждая экспонента зависит от произвольной фазовой постоянной. Начиная с работы Хироты [6, с. 1193] и работ многих других авторов [2, с. 108], эти фазовые постоянные считались вещественными постоянными, не имели особенностей и не зависели от физических параметров солитона, таких как амплитуда и скорость. Однако, если рассматривать фазовые постоянные в солитонных решениях в виде определенных несингулярных функций физических параметров солитона [1, с. 222] , тогда можно получить новый класс точных решений в виде рациональных функций по пространственной переменной х и времени t .
В данной статье мы построим новое точное решение уравнения КдФ, выбрав, фазовые постоянные в виде определенных сингулярных функций параметров солитона — вырожденное солитонное решение ( полиномиально-экспоненциальное решение, имеющее сингулярную особенность).
Рассмотрим двухсолитонное решение [2, с. 1192] уравнения (1):
![]() (2)
(2)
![]() (3)
(3)
где ![]() ;
; ![]() (i=1,2) — произвольные ограниченные вещественные постоянные и
(i=1,2) — произвольные ограниченные вещественные постоянные и 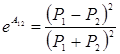 .
.
Предположим, что фазовые постоянные являются сингулярными функциями параметров солитона :
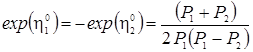 ;
;
тогда выражение (3) можно записать в виде
 .
.
В пределе ![]() мы получаем простейшее вырожденное солитонное — решение уравнения КдФ:
мы получаем простейшее вырожденное солитонное — решение уравнения КдФ:
 . (4)
. (4)
Отметим, что в работе Хусаиновой (Безматерных) и Борисова [5, с. 6] были поострены с помощью метода Хироты [6, с. 1192] более сложные вырожденные солитонные решения для уравнения КдФ.
Данное решение является сингулярным. Действительно, с учетом (2) и (4) имеем
 . (5) ,
. (5) ,
где ![]() ,
, ![]() , (
, (![]() — произвольные постоянные).
— произвольные постоянные).
Видно, что в момент времени t = 0 при ![]() функция u(x, 0) имеет особенность в точке x = 0. Положение данной сингулярной точки в момент времени t задается уравнением
функция u(x, 0) имеет особенность в точке x = 0. Положение данной сингулярной точки в момент времени t задается уравнением
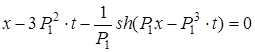 . (6)
. (6)
Заменой ![]() данное уравнение приводится к виду
данное уравнение приводится к виду
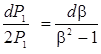 .
.
После интегрирования получаем:
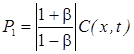 ,
,
где: C(x, t) — неизвестная функция.
Рассмотрим случай ![]() :
:
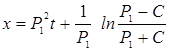 (P1 > 0)
(P1 > 0)
или
 () . (7)
() . (7)
Анализ данного выражения показывает, что при больших t
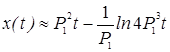 . (8)
. (8)
Поскольку второй член в данном выражении значительно меньше первого, то видно, что при больших t движение особой точки близко к прямолинейному и равномерному движению. На Рис. 1 приведено численное решение уравнения(6).

Рисунок 1 Эволюция особой точки вырожденного солитонного решения (6) (Р1=1,5)
Видно, что при малых t движение особой точки носит сложный характер. Оценки (7) показывают, что при малых t
 .
.
Таким образом, мы показали, что вырожденное солитонное решение уравнения КдФ (5) является сингулярным. Оно образовалось в результате резонансного взаимодействия двух солитонов (параметры двух солитонов в пределе![]() совпадали).
совпадали).![]() Физическая интерпретация данного резонансного решения, как, впрочем, и других известных резонансных (сингулярных) решений уравнения КдФ [3, с. 2182; 4, с. 25; 7, с. 445], пока не вполне ясна и требует дополнительного исследования поведения подобных резонансных решений для соответствующей дискретной цепочки.
Физическая интерпретация данного резонансного решения, как, впрочем, и других известных резонансных (сингулярных) решений уравнения КдФ [3, с. 2182; 4, с. 25; 7, с. 445], пока не вполне ясна и требует дополнительного исследования поведения подобных резонансных решений для соответствующей дискретной цепочки.
Список литературы:
1.Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.; Мир, 1987 — 478 с.
2.Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М: Мир, 1988 — 694 с.
3.Ablowitz M.J., Satsuma J. Solitons and rational solutions of nonlinear evolution equations// J.Math. Phys., — 1978 — Vol. 19 — № 10 — p. 2180—2186.
4.Adler M., Moser J. On a class of polynomials connected with the Korteweg — de Vries equation// Comm.Math.Phys., — 1978 — Vol. 61 — p. 1—30.
5.Bezmaternih G.V. (Khusainova G.V.), Borisov A.B. Rational Exponential Solutions of Nonlinear Equations// Lett.Math.Physics, — 1989 — Vol. 18 — p. 1—8.
6.Hirota R. Exact solution of the Korteweg — de Vries equation for multiple collisions of solitons// Phys. Rev. Lett., — 1971, — Vol. 27 — p. 1192—1194.
7. Nimmo J.J.C., Freeman N.C. Rational solutions of the Korteweg — de Vries equation: wronskian form// Phys.Lett.A, — 1983, — Vol. 96 — № 9 — p. 443—447.
дипломов


Оставить комментарий