СОСТАВЛЕНИЕ  ДИФФЕРЕНЦИАЛЬНОГО  УРАВНЕНИЯ  ПО  УСЛОВИЮ  ФИЗИЧЕСКОЙ  ЗАДАЧИ

Смакова  Фаниля  Фиргатовна

студент  2  курса  физико-математического  факультета  Стерлитамакского  филиала  Башкирского  государственного  университета,  РФ,  г.  Стерлитамак

E -mail:  mouse.minny2009@yandex.ru

Сабитова  Юлия  Камилевна

канд.  физ.-мат.  наук,  доцент  кафедры  математического  анализа  Стерлитамакского  филиала  Башкирского  государственного  университета,  РФ,  г.  Стерлитамак

E-mail: 

DRAWING  UP  THE  DIFFERENTIAL  EQUATION  ACCORDING  TO  A  CONDITION  OF  A  PHYSICAL  TASK

Smakova  Fanilya

student  of  2  years  of  training  of  physical  and  mathematical  faculty  of  Sterlitamak  branch  of  the  Bashkir  State  University,  Russia,  Sterlitamak

Sabitova  Julia

candidate  of  physical  and  mathematical  Science,  assistant  professor  of  the  mathematical  analysis  of  Sterlitamak  branch  of  the  Bashkir  State  University,  Russia,  Sterlitamak

АННОТАЦИЯ

В  данной  работе  приведен  алгоритм  составления  дифференциального  уравнения  по  условию  физической  задачи.  Решена  физическая  задача  на  установление  закона  изменения  физических  величин  с  помощью  дифференциального  уравнения.

ABSTRACT

In  this  article  the  algorithm  of  drawing  up  the  differential  equation  according  to  condition  of  physical  task.  Physical  example  on  establishment  of  the  law  of  change  of  physical  quantities  by  means  of  the  differential  equations  is  reviewed. 

Ключевые  слова:  дифференциальное  уравнение;  алгоритм.

Keywords :  differential  equation,  algorithm.

Дифференциальные  уравнения  являются  одним  из  основных  средств  для  математического  решения  практических  задач.  Особенно  широко  они  используются  в  теоретической  механике  и  физике  [1,  c.  39],  [2,  с.  391].  Решение  задач  физики  с  помощью  дифференциальных  уравнений  состоит  из  трех  этапов:  а)  составление  дифференциального  уравнения;  б)  решения  этого  уравнения;  в)  исследования  полученного  решения.  Удобнее  воспользоваться  следующим  алгоритмом  действий:

1.  установить  изменяющиеся  в  данном  явлении  величины,  выявить  физические  законы,  которые  связывают  их;

2.  выбрать  независимую  переменную  и  функцию  этой  переменной,  которую  необходимо  найти;

3.  по  условию  задачи  определить  начальные  или  краевые  условия;

4.  выразить  все  фигурирующие  в  условии  задачи  величины  через  независимую  переменную,  искомую  функцию  и  ее  производные;

5.  составить  дифференциальное  уравнение  по  условию  задачи  и  физическому  закону;

6.  найти  общее  решение  или  общий  интеграл  дифференциального  уравнения;

7.  найти  частное  решение;

8.  исследовать  полученное  решение.

В  течение  малого  промежутка  времени  величины  изменяются  с  постоянной  скоростью.  Данное  свойство  позволяет  применить  известные  физические  законы,  которые  описывают  равномерно  протекающие  явления,  для  составления  соотношения  между  значениями  ,  т.  е.  величинами,  участвующими  в  процессе  и  их  приращениями.  Но  равенства  будут  иметь  лишь  приближенное  значение.  Если  требуется  получить  точное  решения,  то  следует  разделить  обе  части  получившегося  равенства  на    и  перейти  к  пределу,  когда    стремится  к  нулю.  Получившееся  равенство  содержит:  время  ,  меняющиеся  с  течением  времени  физические  величины  и  их  производные  —  являются  дифференциальным  уравнением,  которое  описывает  данное  явление.  Существует  также  второй  способ  для  получения  дифференциального  уравнения.  Он  заключается  в  замене  приращения    на  дифференциал  ,  а  приращение  функций  —  соответствующими  дифференциалами.

Рассмотрим  конкретный  пример.

Задача.   Парашютист  падает  под  действием  силы  тяжести.  Сопротивление  воздуха  пропорционально  скорости  его  падения,  вначале  падения  он  находился  на  высоте    и  в  состоянии  покоя.  Найти  закон  изменения  высоты  парашютиста  над  уровнем  земной  поверхности.

Решение.  Воспользуемся  вторым  законом  Ньютона:.  Выберем  вертикальное  направление  оси.  Тогда.  Сила  тяжести  направлена  в  отрицательном  направлении,  а  сила  сопротивления  воздуха  направлена  в  сторону,  противоположную  скорости  падения.  Таким  образом,  равенство    принимает  вид:  .  Известно,  что  ускорение  является  производной  от  скорости  ,  тогдаполучаем  следующее  дифференциальное  уравнение  ,  т.  е. 

По  условию  известно,  что  .  Разделяя  переменные  в  уравнении  (1)  и  интегрируя,  находим:

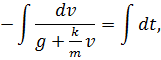
далее

Вычислим  значение  произвольной  постоянной  используя  значение    Так  как  при    значение  ,  то  .  Подставляя  значение    в  (2),  получим

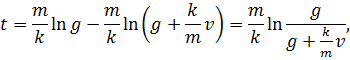
или    Следовательно

Формула  (3)  представляет  собой  закон  изменения  скорости  с  течением  времени.  Найдем  закон  изменения  высоты    парашютиста,  так  как,  то  получим  следующее  дифференциальное  уравнение

Из  (4)  следует

По  условию  при    высота    равна  H.  Подставим  эти  значения  в  (5),  получим,  что    и  тогда

Закон  определения  высоты  парашютиста  над  уровнем  земной  поверхности  при  заданных  условиях  определяется  формулой  (6).  Исследуя  формулу  (6),  можно  прийти  к  следующим  выводам.  Воспользуемся  формулой  Тейлора  для  функции    и  при  малых  значениях    будем  иметь:

Сохраняя  лишь  первые  два  слагаемых,  получаем  из  формулы  (3),  что  .  Это  показывает,  что  в  начале  движения  парашютист  движется  почти  равноускоренно.  В  дальнейшем  влияние  сопротивления  воздуха  становится  ощутимым,  и  при    имеем:  ,  а  потому    стремится  к  .  Движение  становится  почти  равномерным  со  скоростью  ,  направленной  вниз.  Эта  скорость  пропорциональна  силе  тяжести  ,  действующей  на  парашютиста,  и  обратно  пропорциональна  коэффициенту    показывающему  силу  сопротивления  воздуха.  Из  формулы  (6)  можно  приближенно  найти  время,  за  которое  парашютист  упадет  на  земную  поверхность.  Для  этого  учтем,  что

и  напишем  по  формуле  (6)  приближенное  равенство  .  Из  него  находим,  что  .  Заметим,  что  слагаемое    равно  времени,  которое  заняло  бы  падение  парашютиста  с  постоянной  скоростью  ,  а  добавка    произошла  потому,  что  вначале  падение  было  более  медленным.  При  решении  задачи  было  сделано  предположение  о  пропорциональности  силы  сопротивления  воздуха  скорости  падения.  Оно  было  приближенным.  Если  считать  эту  силу  пропорциональной  квадрату  скорости  падения,  то  уравнение  (1)  заменится  на  линейное  неоднородное  дифференциальное  уравнение  вида

,

здесь  направление  силы  сопротивления  воздуха  при  выбранном  направлении  оси  положительно.

Список  литературы:

1.Виленкин  Н.Я.,  Доброхотова  М.А.,  Сафонов  А.Н.  Дифференциальные  уравнения:  учебное  пособие.  М.:  Просвещение,  1984.  —  102  с.

2.Сабитов  К.Б.  Функциональные,  дифференциальные  и  интегральные  уравнения:  учебное  пособие.  М.:  Высш.  шк.,  2005.  —  671  с.