ОПЕРАЦИИ  ЛОГИКИ  В  БИНАРНЫХ  ОТНОШЕНИЯХ

Нестерова  Лариса  Юрьевна

канд.  пед.  наук,  доцент  Арзамасского  филиала  Нижегородского  государственного  университета  им.  Н.И.  Лобачевского,  РФ,  г.  Арзамас

E-mail: 

LOGIC  OPERATIONS  IN  THE  BINARY  RELATIONS

Nesterova  Larisa  Yurevna

edging.  pedagogical  sciences,  the  associate  professor  of  the  Arzamas  branch  of  the  Nizhny  Novgorod  state  university  of  N.I.  Lobachevsky ,  Russia  Arzamas

АННОТАЦИЯ

Рассмотрено  применение  операций  логики  при  проверке  свойств  бинарных  отношений.  Особое  место  отводится  доказательству  свойств  антирефлексивности  и  транзитивности  бинарных  отношений.  Именно  знание  законов  логики,  в  частности,  операции  импликации,  позволяет  сделать  правильный  вывод  в  установлении  указанных  свойств. 

ABSTRACT

  Application  of  operations  of  logic  when  checking  properties  of  the  binary  relations  is  considered.  The  special  place  is  allocated  for  the  proof  of  properties  of  anti-reflexivity  and  transitivity  of  the  binary  relations.  The  knowledge  of  laws  of  logic,  in  particular,  implication  operations,  allows  to  draw  the  correct  conclusion  in  establishment  of  the  specified  properties.

Ключевые  слова:  бинарные  отношения;  операции  над  высказываниями;  свойства  бинарных  отношений.

Keywords:  binary  relations;  operations  over  statements;  properties  of  the  binary  relations

Рассмотрим  бинарные  отношения.  Укажем  основные  пять  свойств:  рефлексивность,  антирефлексивность,  симметричность,  антисимметричность  и  транзитивность.

Рефлексивность: 

Антирефлексивность: 

Симметричность: 

Антисимметричность: 

Транзитивность: 

Для  правильного  определения  свойств  бинарных  отношений  рассмотрим  основные  операции  над  высказываниями:  отрицание,  конъюнкция,  дизъюнкция,  импликация,  эквиваленция.  Результаты  операций  приведем  в  таблице  №  1,  в  которой  истинное  высказывание  обозначим  —  И,  ложное  —  Л  . 

Таблица  1 .

Результаты  операций  логики

Проверим  выполнимость  основных  свойств  бинарных  отношений:

1. 

1.1.             Рефлексивность:  .  Данное  неравенство  верно  для  любого  х.  Рефлексивность  верна.

1.2.             Антирефлексивность:  .  Неравенство  неверно,  приведем  пример  5>5  (Л).  Антирефлексивность  не  выполняется.

1.3.  .  Для  того,  чтобы  доказать,  что  симметричность  не  выполняется  используем  значения  таблицы  №1,  на  пересечении  шестого  столбца  и  четвертой  строки  имеем: .  В  соответствии  с  этим  приводим  пример,  в  котором  посылка  истина,  а  заключение  ложно.    (И),  но    (Л),  следовательно,  импликация  ложна.  Симметричность  не  выполняется.

1.  4.  Антисимметричность:    Необходимо  установить  при  каких  условиях  посылки  будет  ложной  или  истиной.  Посылка  состоит  из  двух  высказываний,  которые  связаны  операцией  конъюнкцией  (таблица  №  1,  столбик  четвертый).  Результат  этой  операции  истинный  только  в  одном  случае,  когда  оба  утверждения  истины.  Если  это  так,  то  посылка  будет  истина.  Однако,  в  остальных  случаях  результат  операции  будет  ложен.  Отметим,  что  в  этом  случае  либо  первое,  либо  второе  высказывания  ложны.  Таким  образом,  посылка  будет  ложна  и  в  соответствии  с  определением  операции  импликации  (шестой  столбик),  не  зависимо  от  заключения,  импликация  принимает  только  истинное  значения.  Однако,  в  частном  случае  получаем:  при 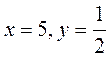 следующее  высказывание,  которое  является  истинным:  .  Без  знаний  операций  логики  установить  истинность  данного  высказывания  проблематично.

Антисимметричность  выполняется.

1.  5.  Транзитивность: 

Транзитивность  выполняется  по  свойству  неравенств,  так  как 

Данное  бинарное  отношение:  рефлексивно,  антисимметрично  и  транзитивно.

2. 

2.  1.  Рефлексивность:  .  Данное  неравенство  верно  для  любого  х.  Рефлексивность  верна.

2.  2.  Антирефлексивность:  .  Неравенство  неверно,  приведем  пример  16:16(Л).  Антирефлексивность  не  выполняется.

2.  3.  Симметричность:  .  Для  того,  чтобы  доказать,  что  симметричность  не  выполняется  используем  значения  таблицы  №  1  (столбик  6),  приведем  следующий  пример  .  Видим,  что  посылка  истина,  а  заключение  ложно.  По  таблицы  результат  импликации  ложен.  Симметричность  не  выполняется.

  2.  4.  Антисимметричность:  Используем  аналогичные  рассуждения,  что  и  при  проверке  симметричности,  получим:    . 

Антисисмметричность  не  выполняется.

2.  5.  Транзитивность: 

.  Докажем,  что  транзитивность  имеет  место.  Если  ,  тогда  можно  записать  ,  подставим  у  из  (2)  уравнения  в  первое,  получим  ,  следовательно,  .  Транзитивность  имеет  место.

Бинарное  отношение  —  рефлексивно  и  транзитивно.

3. 

3.1.             Рефлексивность:  .  Данное  неравенство  неверно  для  любого  х,  приведем  пример  10+5<5  (Л). 

Рефлексивность  неверна.

3.  2.  Антирефлексивность:  .  Неравенство  верно  не  для  любого  x,  ,преобразуем  неравенство,  следовательно,  ,  неравенство  верно.  Антирефлексивность  выполняется.

3.  3.  Симметричность:  .  Для  того,  чтобы  доказать,  что  симметричность  не  выполняется  используем  значения  таблицы  №1,  приведем  следующий  пример  ,  получим    Видим,  что  посылка  истина,  а  заключение  ложно.  Симметричность  не  выполняется.

  3.  4.  Антисимметричность:    Преобразуем  посылку:  к  неравенству  ,  к  левой  и  правой  частям  прибавим  число5,  получим,  по  свойству  неравенств  запишем  ,  после  преобразований  имеем  ,следовательно,  10<0.  Таким  образом,  посылка  всегда  ложна,  а  результат  импликации  истинный. 

Антисимметричность  выполняется.

3.  5.  Транзитивность: 

.  Докажем,  что  транзитивность  имеет  место.  Прибавим  к  левой  и  правой  частям  неравенства  (1)  число  5,  получим  ,  запишем    по  свойству  неравенств  имеем  .  Сравним  множество  решений  (4)  и  (3)  неравенств.  Неравенство  (4)  имеет  решение  ,  а  (3)  —  .  Если  выполняется  (5),  то  (6)  будет  иметь  место  автоматически,  следовательно,  транзитивность  верна.

Бинарное  отношение  —  антирефлексивно,  антисимметрично  и  транзитивно.

4. 

4.1.             Рефлексивность:  .  Данное  неравенство  неверно  для  любого  х,  приведем  пример  (Л).  Рефлексивность  неверна.

4.2.             Антирефлексивность:  .  При    получим,(Л).  Антирефлексивность  не  выполняется.

4.3.  Симметричность:  .  Для  любых  действительных  чисел  имеет  место  коммутативность  умножения,  то  есть  .  Симметричность  выполняется.

4.  4.  Антисимметричность:    Приведем  пример  (таблица  1),  при  котором  посылка  истина,  а  заключение  ложно:  .  Антисимметричность  не  выполняется.

4.  5.  Транзитивность: 

.  Докажем,  что  транзитивность  не  выполняется.  Приведем  пример:  (Л),  следовательно,  транзитивность  не  имеет  место.

Бинарное  отношение  —  симметрично.

5. 

5.1.             Рефлексивность:.

  Данное  неравенство  неверно  для  любого  х,  приведем  пример 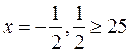 (Л).  Рефлексивность  неверна.

5.  2.  Антирефлексивность:  .  Неравенство  верно,  но  не  для  любого  x,  (Л).

Антирефлексивность  неверна.

5.  3.  Симметричность:  .  Для  любых  действительных  чисел  имеет  место  коммутативность  умножения,  то  есть  .  Симметричность  выполняется.

5.  4.  Антисимметричность:    Рассмотрим  случай,  когда  тогда 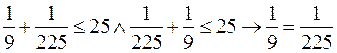 .  Получили  высказывание  вида  .  Антисимметричность  не  выполняется.

5.  5.  Транзитивность: 

.  Докажем,  что  транзитивность  не  выполняется.  Приведем  пример:  ,  тогда  ,  следовательно,  транзитивность  не  имеет  место.

Бинарное  отношение  —  симметрично.

Использование  операций  логики  при  проверке  свойств  бинарных  отношений  позволяет  сделать  правильный  вывод.  Особое  внимание  следует  обратить  на  доказательство  свойств  антирефлексивности  и  транзитивности  бинарных  отношений,  так  как  в  частных  случаях,  при  конкретных  значениях  х,  у,  z  получаем  высказывания  истинность  или  ложность,  которых  установить  достаточно  проблематично.  Именно  знание  законов  логики,  в  частности,  операции  импликации,  позволяет  сделать  правильный  вывод  в  установлении  указанных  свойств. 

Список  литературы:

1.Куликов  Л.Я.  Алгебра  и  теория  чисел:  учеб.  пособие.  М.:  Высшая  школа,1979.  —  559  с.

2.Шнеперман  Л.Б.  Сборник  задач  по  алгебре  и  теории  чисел:  учеб.  пособие.  Изд-во:  Лань,  2008.  —  224  с.