Статья опубликована в рамках: XVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 02 апреля 2014 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦЫ ЯКОБИ ОДНОЙ ![]() -МЕРНОЙ СИСТЕМЫ
-МЕРНОЙ СИСТЕМЫ
Рузич Роман Васильевич
аспирант Хмельницкого национального университета, Украина, г. Хмельницкий
FEATURES OF DETERMINING THE EIGENVALUES OF JACOBI MATRIX OF SOME ![]() -DIMENTIONAL SYSYEM
-DIMENTIONAL SYSYEM
Roman Ruzich
post-graduate student, Khmelnitsky National University, Ukraine, Khmelnitsky
АННОТАЦИЯ
Проблема собственных значений является достаточно сложной и не полностью решенной, особенно в случае параметрической матрицы. В работе рассматривается многомерная модель разомкнутого гиперцикла Эйгена. Показан алгоритм определения собственных значений матрицы Якоби в некоторых особых точках.
ABSTRACT
The eigenvalue problem is complicated and not fully resolved, especially in the case of parametric matrix. We consider the multidimensional model of open Eigen’s hypercycle. Algorithm for determining the eigenvalues of the Jacobi matrix in some stationary points is demonstrated.
Ключевые слова : собственное значение; матрица Якоби; модель разомкнутого гиперцикла Эйгена.
Keywords : eigenvalue; the Jacobi matrix; the model of open Eigen’s hypercycle.
Целый ряд процессов, происходящих в окружающем мире, описываются системами нелинейных дифференциальных уравнений. В основном решения таких систем трудно (а за частую и не возможно) найти в квадратурах. Поэтому для их исследования используются методы качественного анализа. Как известно, исследования локального поведения траекторий основано на рассмотрении матрицы Якоби и оценки ее собственных значений в стационарных точках.
Если для двумерной системы это является тривиальной задачей, то для ![]() -мерного случая раскрытие соответствующего определителя и решение уравнения
-мерного случая раскрытие соответствующего определителя и решение уравнения ![]() -ой степени является достаточно сложной задачей [3]. На данный момент разработано достаточно много методов определения собственных значений матрицы: как итерационных [1, 6—9], так и таких, которые заключаются в преобразовании начального определителя [1, 4]. Однако следует отметить, что в случае, когда коэффициенты исходной системы дифференциальных уравнений задано параметрически, то существующие методы решения задач на собственные значения не слишком помогают.
-ой степени является достаточно сложной задачей [3]. На данный момент разработано достаточно много методов определения собственных значений матрицы: как итерационных [1, 6—9], так и таких, которые заключаются в преобразовании начального определителя [1, 4]. Однако следует отметить, что в случае, когда коэффициенты исходной системы дифференциальных уравнений задано параметрически, то существующие методы решения задач на собственные значения не слишком помогают.
В работе мы рассмотрим модель разомкнутого гиперцикла Эйгена [2, 5], которая используется для описания сукцессий в биогеоценозах:
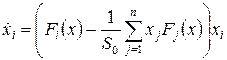 ,
, ![]() , (1)
, (1)
где ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Здесь
. Здесь ![]() — популяционная переменная, численность (концентрация или биомасса)
— популяционная переменная, численность (концентрация или биомасса) ![]() -ой ассоциации,
-ой ассоциации, ![]() ;
; ![]() — коэффициент, определяющий численность первой ассоциации в состоянии равновесия при отсутствии второй;
— коэффициент, определяющий численность первой ассоциации в состоянии равновесия при отсутствии второй; ![]() — коэффициент, отражающий зависимость
— коэффициент, отражающий зависимость ![]() -ой ассоциации от
-ой ассоциации от ![]() -ой,
-ой, ![]() ;
; ![]() — емкость среды (размер экологической ниши).
— емкость среды (размер экологической ниши).
В этой статье рассмотрим особенности исчисления и анализа собственных значений матрицы Якоби в стационарных точках модели (1).
Обозначим полиномы в правой части системы (1) как ![]() , запишем их производные по переменной
, запишем их производные по переменной ![]() как
как
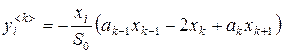 ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() , (2)
, (2)
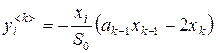 ,
, ![]() ,
, ![]() , (3)
, (3)
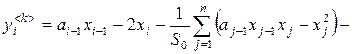
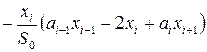 ,
, ![]() ,
, ![]() , (4)
, (4)
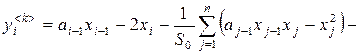
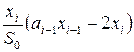 ,
, ![]() , (5)
, (5)
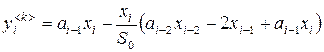 ,
, ![]() ,
, ![]() . (6)
. (6)
Можем записать структуру ![]() -ой (
-ой (![]() ) строки матрицы Якоби системы (1):
) строки матрицы Якоби системы (1):
![]()
где ![]() ,
, 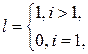
![]() ,
, 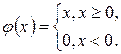
Теорема 1. Если координата ![]() особой точки равна нулю, то одно из собственных значений матрицы Якоби в этой точке вычисляется как
особой точки равна нулю, то одно из собственных значений матрицы Якоби в этой точке вычисляется как
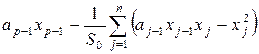 (7)
(7)
при условии, что ![]() — первая координата или предшествующая
— первая координата или предшествующая ![]() координата не нулевая, и как
координата не нулевая, и как
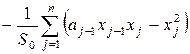 (8)
(8)
в противном случае.
Доказательство. Пусть некоторая координата ![]() особой точки равна нулю. Тогда строку
особой точки равна нулю. Тогда строку ![]() матрицы Якоби можем записать как
матрицы Якоби можем записать как
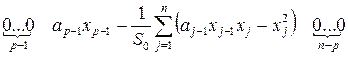
Определим характеристическое уравнение матрицы Якоби в этой точке как ![]() , где
, где ![]() — матрица Якоби,
— матрица Якоби, ![]() — единичная матрица,
— единичная матрица, ![]() — собственные значения. Тогда разложение определителя на алгебраические дополнения по строке
— собственные значения. Тогда разложение определителя на алгебраические дополнения по строке ![]() можно записать как
можно записать как
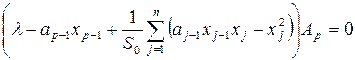 ,
,
где: ![]() — минор по диагональному элементу, который находится в строке
— минор по диагональному элементу, который находится в строке ![]() определителя. Таким образом, одно собственное значение может быть рассчитано как
определителя. Таким образом, одно собственное значение может быть рассчитано как 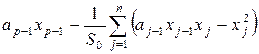 или
или 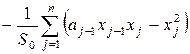 в случае
в случае ![]() . Теорема доказана.
. Теорема доказана.
Рассматривая систему (1), можно заметить, что приравняв ![]() к нулю, другие
к нулю, другие ![]() координаты особой точки вычисляются как для
координаты особой точки вычисляются как для ![]() -мерной системы. Далее приравняем
-мерной системы. Далее приравняем ![]() к нулю, тогда другие
к нулю, тогда другие ![]() координаты вычисляются как для
координаты вычисляются как для ![]() -мерной системы и т. д. Рассматривая процесс в обратном порядке, можем утверждать следующее: если ко всем особым точкам
-мерной системы и т. д. Рассматривая процесс в обратном порядке, можем утверждать следующее: если ко всем особым точкам ![]() -мерной модели добавить
-мерной модели добавить ![]() -у нулевую координату, то в образованных точках будет равно нулю векторное поле и
-у нулевую координату, то в образованных точках будет равно нулю векторное поле и ![]() -мерной системы. Подобные точки равновесия будем называть точками «потомками».
-мерной системы. Подобные точки равновесия будем называть точками «потомками».
Запишем последнюю строку матрицы Якоби в подобной точке (с последней нулевой координатой)
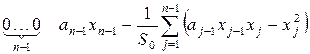 .
.
Клетка, включающая первые ![]() строки и
строки и ![]() столбца, соответственно к формулам (2), (4), (6) не отличается от общего случая, причем элементы главной диагонали можно записать как
столбца, соответственно к формулам (2), (4), (6) не отличается от общего случая, причем элементы главной диагонали можно записать как
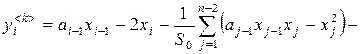
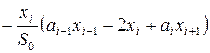 ,
, ![]() ,
, ![]() .
.
Элементы ![]() -ой строки клетки, состоящей из первых
-ой строки клетки, состоящей из первых ![]() строк и
строк и ![]() столбцов полученной матрицы Якоби, определяются как
столбцов полученной матрицы Якоби, определяются как
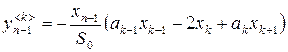 ,
, ![]() ;
;
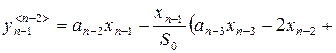
![]() ;
;
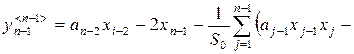
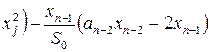 ;
;
а элементы последнего столбца этой клетки как
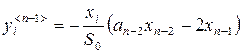 ,
, ![]() .
.
Таким образом ![]() клетка является матрицей Якоби
клетка является матрицей Якоби ![]() -мерной модели разомкнутого гиперцикла Эйгена в точке, образованной отбрасыванием последней координаты (которая является нулем) особой точки
-мерной модели разомкнутого гиперцикла Эйгена в точке, образованной отбрасыванием последней координаты (которая является нулем) особой точки ![]() -мерной модели. Полученный результат можем сформулировать в форме следующей теоремы.
-мерной модели. Полученный результат можем сформулировать в форме следующей теоремы.
Теорема 2. ![]() собственные значение матрицы Якоби в точка «потомках»
собственные значение матрицы Якоби в точка «потомках» ![]() -мерной модели разомкнутого гиперцикла Эйгена определяются как собственные значения матрицы Якоби в соответствующих точках
-мерной модели разомкнутого гиперцикла Эйгена определяются как собственные значения матрицы Якоби в соответствующих точках ![]() -мерной системы, а еще одно собственное значение равно
-мерной системы, а еще одно собственное значение равно
![]()
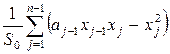 .
.
Следствие 2.1. ![]() собственные значения матрицы Якоби в точке последними
собственные значения матрицы Якоби в точке последними ![]() нулевыми координатами определяются с
нулевыми координатами определяются с ![]() -мерной модели,
-мерной модели, ![]() за формулой (8), а одно равно
за формулой (8), а одно равно
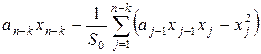 . (9)
. (9)
Рассмотрим особые точки модели (1) с не более чем двумя ненулевыми координатами, при условии что, по крайней мере, после одной нулевой координаты существует одна ненулевая. Были определены следующие множества особых точек
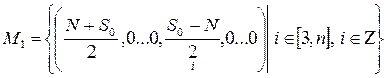 ,
,
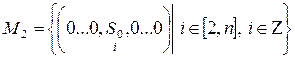 ,
,
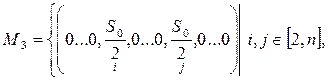
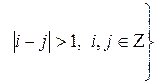 ,
,
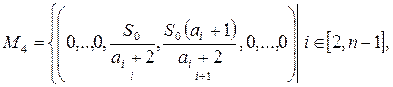
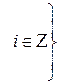 .
.
Используя теоремы 1, 2 и следствие 2.1 легко показать, что в точках из множества ![]() собственные значения матрицы Якоби вычисляются как
собственные значения матрицы Якоби вычисляются как ![]()
![]()
![]()
![]() ; в точках с множества
; в точках с множества ![]() –
– ![]()
![]()
![]() (
(![]() ); в точках с множества
); в точках с множества ![]() –
– ![]()
![]()
![]()
![]()
![]() ; в точках с множества
; в точках с множества ![]() –
– ![]()
![]()
![]()
![]()
Проанализировав полученные собственные значения, можем отметить, что точки из множеств ![]() —
—![]() подтверждают выдвинутую в работе [2] гипотезу: если справа от нулевой координаты особой точки модели разомкнутого гиперцикла Эйгена существует ненулевая координата, то такая точка неустойчива при любых положительных значениях параметров.
подтверждают выдвинутую в работе [2] гипотезу: если справа от нулевой координаты особой точки модели разомкнутого гиперцикла Эйгена существует ненулевая координата, то такая точка неустойчива при любых положительных значениях параметров.
Список литературы:
1.Березин И.С., Жидков Н.П. Методы вычислений. Том II. М.: Физматгиз, 1962. — 640 с.
2.Рузич Р.В. Стійкість особливих точок трьохвимірного випадку однієї моделі екологічної макросистеми // Вісник Одеського національного університету. Математика і механіка. — 2012. — Т. 17, — вип. 3 (15). — С. 45—51.
3.Уилкинс Дж.Х. Алгебраическая проблема собственных значений. М.: Наука, 1970. — 564 c.
4.Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. 3-е стереот. изд. СПб.: Лань, 2002. — 736 с.
5.Чернишенко С.В. Нелинейные методы динамики лесных биогеоценозов. Днепропетровск: Изд-во ДНУ, 2005. — 500 с.
6.Egana J.C., Kuhl N.M., Santos L.C. An inverse eigenvalue method for frequency isolation in spring-mass systems // Numerical Linear Algebra with Applications. — 2002. — Vol. 9, — Is. 1. — P. 65—79.
7.Golub G.H., Wilkinson J.H. Ill-conditioned eigensystems and the computation of the Jordan canonical form // SIAM Review. — 1976. — Vol. 18, — № 4. — P. 578—619.
8.Ipsen C.F. Computing an eigenvector with inverse iteration // SIAM Review. — 1997. — Vol. 39, — № 2. — P. 254—291.
9.Paige C.C. Computational variants of the Lanczos method for the eigenproblem // Journal of the Institute of Mathematics and Its Applications. — 1972. — № 10. — P. 373—381.
дипломов


Оставить комментарий