ОПИСАНИЕ  ХАОТИЧЕСКИХ  РЕШЕНИЙ  С  ПОМОЩЬЮ  РЯДА  ЛОРАНА  С  СУЩЕСТВЕННОЙ  ОСОБОЙ  ТОЧКОЙ

 Якубовский  Евгений  Георгиевич 

инженер  вычислительного  центра,  Национальный  Минерально-Сырьевой  Университет  «Горный»,  РФ,  г.  Санкт- Петербург

E-mail: 

DESCRIPTION  CHAOTIC  SOLUTIONS  USING  LAURENT  SERIES  WITH  AN  ESSENTIAL  SINGULARITY

Jakubowski  Evgeny

engineering  Computer  Center,  National  University  of  Mineral-Raw  "Mountain",  Russia  St.  Petersburg

АННОТАЦИЯ

Эволюционные  квазилинейные  дифференциальные  уравнения  сводятся  к  системе  обыкновенных  нелинейных  дифференциальных  уравнений.  В  статье  [2]  исследовано  их  решение  в  случае  не  кратных  положений  равновесия.  В  предлагаемой  статье  исследованы  эти  уравнения  в  случае  кратных  положений  равновесия. 

ABSTRACT

Evolutionary  quasilinear  differential  equations  reduce  to  a  system  of  nonlinear  ordinary  differential  equations.  We  studied  these  equations  in  [2],  in  the  cases,  when  equilibrium  positions  are  onefold.  In  this  paper  we  studied  these  equations  in  the  case  of  multiple  equilibrium  position. 

Ключевые  слова :  хаотические  решения;  ряд  Лорана  с  существенно  особой  точкой;  кратные  положения  равновесия. 

Keywords :  chaotic  solutions;  Laurent  series  with  an  essential  singularity;  multiple  equilibrium  position.

Лемма  1.  Сумма  коэффициентов 

по  индексу    равна  нулю,  т.е.  .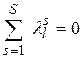 

Для  доказательства  этого  тождества  рассмотрим  полином    степени  относительно 

,

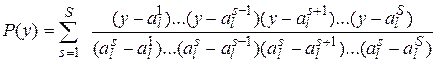В  точках  положения  равновесия    полином  удовлетворяет  .  В  силу  единственности  полинома  степени  ,  проходящего  через    точек,  получаем  ,  так  как  это  значение  удовлетворяет  точкам  аппроксимации.  Распишем  формулу  для  полинома,  равного  единице,  разделив  его  на  произведение  ,  получим

,

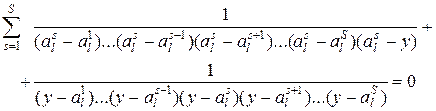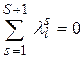полагая,    получим  тождество  ,  в  случае,  если  имеется    положение  равновесия.

  Опишем  структуру  возможно  хаотического  решения,  которое  является  турбулентным  при  кратных  положениях  равновесия.  В  случае  уравнения  Навье-Стокса  кратные  корни,  это  свойство  комплексного  решения,  или  турбулентного  решения. 

Теорема  1.  В  случае  системы  (1)  с  двукратным  корнем  положения  равновесия  решение  задачи  Коши  в  комплексной  плоскости  для  системы  дифференциальных  уравнений  (1)  с  действительными  и  комплексными  положениями  равновесия  будет  определяться  рядом  Лорана  с  существенной  особой  точкой  и,  следовательно,  при  приближении  к  особенности  может  носить  хаотический  характер.  Может  иметь  полюсы  со  знаменателем  ,  где    количество  положений  равновесия.  Положений  равновесия  должно  быть  больше  двух.  В  общем  случае  решение  задачи  не  единственно,  а  имеется  счетное  количество  решений.  Причем  реализуется  состояние  с  наименьшей  энергией.  Аргумент  решения    является  действительным.  Система  дифференциальных  уравнений  (1)  запишется  в  виде

  .  (1)

Доказательство.

Решение  уравнения  (1)  в  случае  кратных  положений  равновесия  исследовалось  в  [3],  [4].  Уточним  эти  решения. 

В  случае  двух  кратного  корня    систему  дифференциальных  уравнений  (1)  можно  представить  в  виде

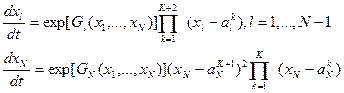  ,  (2)

где  введен  не  обращающийся  в  ноль  множитель  ,  который  равен  .  При  подстановке  этого  множителя  в  (2),  получим  (1).  Покажем,  что  этот  множитель  в  ноль  не  обращается.  Величины    удовлетворяют  условию  ,  где  величина    конечна. 

При  условии    имеем  конечный  предел

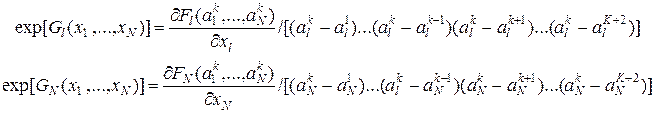
При  условии    тоже  имеем  конечный  предел

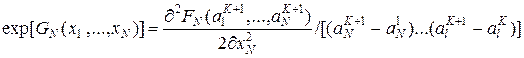
В  случае  совпадающих  корней  сокращается  множитель  .  При  этом  получается  не  обращающийся  в  ноль  множитель  .  При  этом  дифференциал

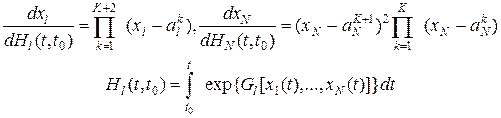,  (3)

где    стремящаяся  к  бесконечности  функция  при  условии  .  В  случае  решения  в  действительной  плоскости  это  монотонная  функция.

Запишем  дифференциальное  уравнение  с  кратным  значением  положения  равновесия

.

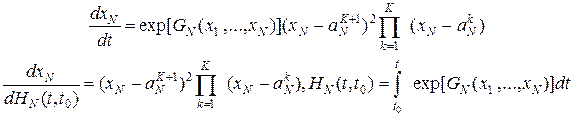Величина    в  ноль  не  обращается.  Решение  этого  дифференциального  уравнения  имеет  вид

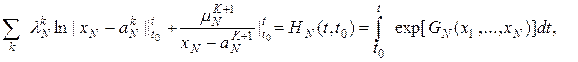    (4) 

  координаты  положения  равновесия,  величина    значение  двух  кратного  положения  равновесия. 

Имеем  три  возможных  варианта  разложения  функции  в  ряд.  Либо  в  точке    имеется  существенная  особая  точка,  и  решение  стремится  к  произвольным  точкам  при  приближении  к  особенности,  либо  справедливо 

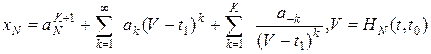  .  (5)

либо  решение  регулярно.  Допустим  справедливо  (5).  Определим  решение  этого  дифференциального  уравнения,  для  чего  подставим  часть  решения  в  виде  полюса 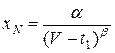   в  уравнение 

  .  (6)

При  этом  оказывается,  что  приравниваются  члены 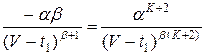 ,  что  приводит  к  равенству    и  для  множителя  справедливо  .  При  этом  решение  при  условии    имеет  сложную  структуру  и  не  имеет  однозначного  решения  в  комплексной  плоскости,  т.  е.  в  точке    имеется  ветвление  решения  и  значит,  возможен  переход  к  комплексному  решению.  Откуда  имеем  .  Т.  е.  решение  в  этом  случае  является  турбулентным,  комплексным  и  имеющим  множество  ветвей.

Допустим,  решение  регулярно.  Разложим  решение  в  окрестности  точки    по  положительным  степеням  ,  т.е.  .  Тогда 

решение  представимо  в  виде  .  Т.  е.  справедлива  формула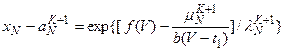 

Т.  е.  предположение  о  регулярности  решения  не  подтверждается,  решение  имеет  бесконечное  число  членов  с  отрицательной  степенью  .  Значит,  решение  имеет  существенную  особую  точку  при  условии  . 

При  этом  решение  с  существенной  особой  точкой  определяется  из  уравнения  (5). 

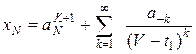    (7)

Причем  решение  конечно  до  координаты  положения  равновесия,  что  следует  из  уравнения  (4),  т.  е.  ряд  (7)  имеет  бесконечный  радиус  сходимости.  Т.  е.  по  мере  приближения  к  положению  равновесия    координаты    величина  ,  что  следует  из  уравнения  (4)  и  (7),  но  при  этом  пересекает  точку  ,  в  которой  происходит  скачок  решения.  Этот  скачок  решения  является  произвольным,  так  как  решение  в  виде  ряда  Лорана  содержит  существенную  особую  точку  и  при  приближении  к  особой  точке,  значение  функции    произвольно  см.  [1]§  10.  В  результате  решения  в  окрестности  кратного  положения  равновесия,  получаются  ряды  Лорана  с  существенной  особой  точкой. 

Причем  коэффициенты  ряда  Лорана  могут  оказаться  многозначной  функцией,  так  же  как  и  решение  в  случае  полюса.

При  этом  многозначное  решение  имеет  вид  ряда  Лорана  и  может  иметь  существенно  особую  точку,  а  может  быть  многозначное  решение  имеет  вид

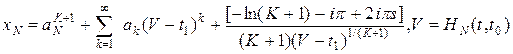  (7)

Выводы

В  случае  кратных  положений  равновесия,  решение  имеет  хаотический  характер.  Оно  определяется  рядом  Лорана  с  существенно  особой  точкой,  и  значит,  по  мере  приближения  аргумента  функции  к  существенно  особой  точке  наблюдается  произвольное  значение  решения. 

Список  литературы:

1.Смирнов  В.И.  Курс  высшей  математики,  т.  III,  ч.  2.,М.:,  «Наука»,  1974  г.,  —  672  с.

2.Якубовский  Е.  Комплексные,  ограниченные  решения  уравнений  в  частных  производных  «Теоретические  и  практические  аспекты  естественных  и  математических  наук»:  Материалы  международной  заочной  научно-практической  конференции.  Новосибирск:  Изд.  «СибАК»,  2012  г.,  —  стр.  19—30.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  www.sibac.info

3.Якубовский  Е.  Решение  уравнения  Навье-Стокса.  Применение  решений  и  следствие  из  них.  LAP  LAMBERT  Academic  Publishing,  2013,  —  102  с.

4.Якубовский  Е.  Турбулентные  течения  в  цилиндрических  трубах.  Экспериментальное  подтверждение  комплексного  решения.  LAP  LAMBERT  Academic  Publishing,  2013,  —  52  с.