ИССЛЕДОВАНИЕ  ДИНАМИКИ  МАЯТНИКОВЫХ  СИСТЕМ  С  ПЕРЕМЕННЫМИ  ПАРАМЕТРАМИ

Старков  Владимир  Николаевич

канд.  физ.-мат.  наук,  доцент  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E-mail:  vlad.stark@yandex.ru

Степенко  Николай  Анатольевич

канд.  физ.-мат.  наук,  доцент  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E-mail: 

STUDY  OF  DYNAMICS  OF  PENDULUM  SYSTEMS  WITH  VARIABLE  PARAMETERS

Vladimir  Starkov

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  Saint  State  University,  Russia  Saint  Petersburg

Nikolay  Stepenko

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  Saint  State  University,  Russia  Saint  Petersburg

АННОТАЦИЯ

Исследуется  динамика  маятниковых  систем  с  переменными  параметрами:  перемещение  точки  подвеса,  изменения  длины  маятника  или  массы  грузика.  Рассмотрены  также  колебания  маятника  при  одновременно  изменении  массы  грузика  и  перемещении  точки  подвеса.  Учитывалось  как  увеличение,  так  и  уменьшение  массы  грузика.  Использовались  численные  методы  решения  и  фазовые  представления  динамических  систем.  Все  расчеты  были  проведены  в  среде  Maple.

ABSTRACT

Dynamics  of  pendulum  systems  with  variable  parameters  is  under  examination  in  the  article:  displacement  of  a  suspension  point,  change  of  a  pendulum  length  or  of  a  weight  mass.  There  are  also  considered  pendulum  oscillations  while  simultaneous  change  of  a  weight  mass  and  displacement  of  a  suspension  point.  An  increase  as  well  as  a  decrease  of  a  weight  mass  has  been  taken  into  account.  Numerical  computations  and  phase  representations  of  dynamic  systems  have  been  used.  All  the  computations  have  been  performed  in  Maple  environment.

Ключевые  слова:  динамика  маятника;  качественный  анализ;  параметрические  колебания.

Keywords:  pendulum  dynamics;  qualitative  analysis;  parametric  oscillations.

Колебательные  процессы  вообще  и  маятниковые  системы,  в  частности,  широко  распространены  в  природе  и  технике  [1,  2].

Известно  уравнение  колебаний  маятника  с  постоянными  параметрами  (  —  масса  грузика,    —  длина  маятника): 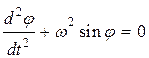 ,  где    —  угол  отклонения  маятника  от  вертикали, 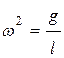 ,    —  ускорение  силы  тяжести.  Для  численного  расчета  задаются  начальные  условия:  при  ,  ,  .

Иногда  в  колебательной  системе  параметры  меняются  по  какому-то  закону,  что  можно  трактовать  как  внешнее  воздействие  на  нее.  Возникновение  колебательного  процесса  из-за  изменения  параметров  называется  параметрическим  возбуждением  колебаний  [3]. 

Будем  исследовать  влияние  на  динамику  колебаний  маятника  изменений  длины  маятника,  массы  грузика,  точки  подвеса  и  их  комбинаций  [4,  5]. 

Рассмотрим  сначала  влияние  горизонтальных  колебаний  точки  подвеса    на  динамику  маятника  (рис.  1,  слева).

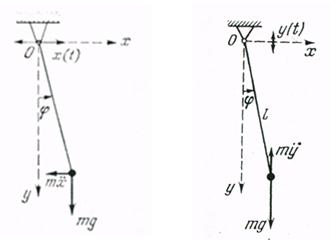
Рисунок  1.  Колебания  точки  подвеса  по  горизонтали  по  закону    (слева)  и  по  вертикали  по  закону  (справа)

Если  ,  где    —  амплитуда  колебаний  точки  подвеса,    —  частота  колебаний,  то  для  угла    уравнение  примет  вид:  .

Рассчитаем  динамику  процесса  и  построим  фазовые  портреты.  Рассмотрим  три  случая:  .

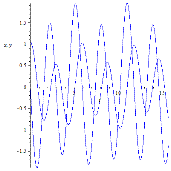
Рисунок  2.  Амплитуда  и  скорость  колебаний  как  функции  времени  для  различных  частот 

Теперь  построим  соответствующие  фазовые  портреты.

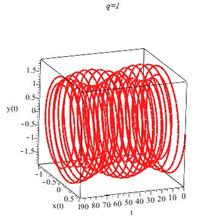
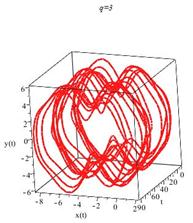
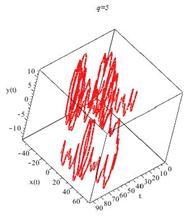
Рисунок  3.  Рост  частоты  колебаний  точки  подвеса  хаотизирует  движение

Рассмотрим  теперь  влияние  вертикальных  перемещений  точки  подвеса  на  динамику  маятника  (рис.  1,  справа).

Если  ,  то  уравнения  движения  маятника

.

Рассчитаем  динамику  процесса  и  построим  фазовые  портреты.  Рассмотрим  три  случая:  .

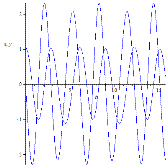
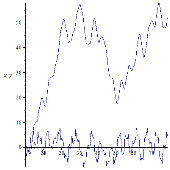
Рисунок  4.  Динамика  для  различных  частот  колебаний  точки  подвеса

Теперь  рассмотрим  соответствующие  фазовые  портреты.

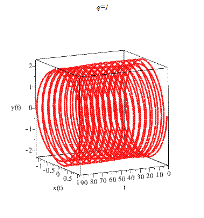
Рисунок  5.  Рост  частоты  колебаний  точки  подвеса  хаотизирует  движение

Уравнение  для  вертикально-горизонтальных  колебаний  точки  подвеса

.

Рассчитаем  динамику  процесса  и  построим  фазовые  портреты.  Рассмотрим  три  случая:  .

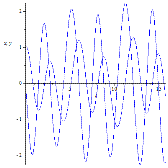
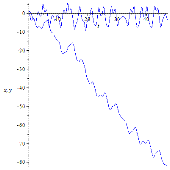
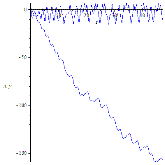
Рисунок  6.  Динамика  для  различных  частот  колебаний  точки  подвеса

Были  рассчитаны  соответствующие  фазовые  портреты

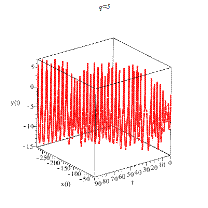
Рисунок  7.  Рост  частоты  колебаний  точки  подвеса  хаотизирует  движение

Далее  проведем  исследование  маятниковых  систем  при  изменяющейся  длине  маятника.  Допустим,  что  по  какой-то  внешней  причине  (от  случайного  толчка)  маятник  совершает  собственные  колебания  с  частотой,  соответствующей  примерно 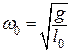 ,  где    —  ускорение  силы  тяжести,    —  первоначальная  длина  маятника.  В  это  же  время  изменяется  и  длина  маятника  [6].

В  этом  случае  уравнение  движения  маятника  с  переменной  длиной  можно  записать  так:    или       .

В  [6]  была  рассмотрена  задача  о  колебаниях  маятника  при  следующих  предположениях:  амплитуды  колебаний  маятника  малы,  т.  е.    и  закон  изменения  длины 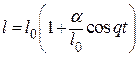 ,  где    —  частота  и    —  амплитуда.

В  нашей  задаче  рассмотрен  случай        ,  когда  при    длина  .  Тогда  имеем  уравнение  в  общем  виде

.

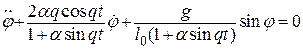Рассмотрим  три  случая:  .

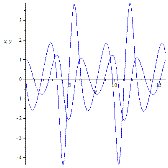
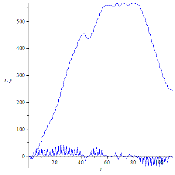
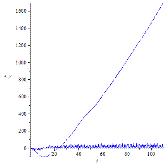
Рисунок  8.  Динамика  маятника  для  различных  частот  колебаний  длины

Теперь  рассмотрим  соответствующие  фазовые  портреты.

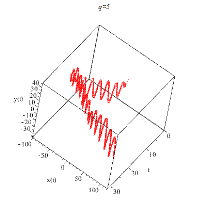
Рисунок  9.  Фазовые  портреты  для  различных  частот

Далее  исследуем  колебания  маятника  при  изменении  массы  грузика.  Висящая  на  нити  однородная  материальная  точка,  являющаяся  в  начальный  момент  времени  шариком  радиуса  ,  имеющим  массу  ,  качается  без  трения  и  постепенно  обмерзает  или  испаряется  (как  в  [7]).

В  этом  случае  уравнение  движения  маятника  переменной  массы  имеет  вид  [7]:

.                                    (1)

Учитывая,  что  массы  шарика  в  разные  моменты  времени  относятся  как  кубы  радиусов,  имеем: 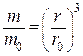 ,  т.е. 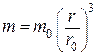 и

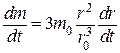.                                                      (2)

Тогда  (1)  примет  вид:

.

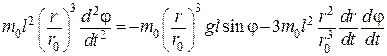По  условию  приращения  массы,  отнесенное  ко  времени,  т.е.  производная  ,  пропорциональна  площади  поверхности  шарика  в  данный  момент:

,                                      (3)

здесь    —  коэффициент  пропорциональности.

Сравнивая  (2)  и  (3),  получаем: 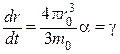 ,  где    —  новая  постоянная.

После  интегрирования  имеем  .  Окончательно  уравнение  движения  принимает  вид  .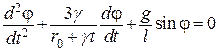

Для  него  построим  фазовые  портреты.

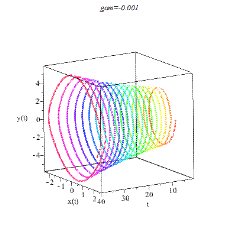
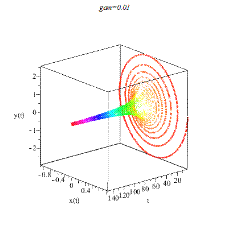
Рисунок  10.  Влияние  уменьшения  массы  грузика  (слева)  и  увеличения  массы  грузика  (справа)  на  колебания  маятника.

Видим,  что  увеличение  массы  грузика  стабилизирует  колебания  маятника.

Теперь  изучим  влияние  перемещения  точки  подвеса  на  колебания  маятника  в  условиях  изменения  массы  грузика.  Учтем,  как  и  ранее,  влияние  вертикальных  колебаний  точки  подвеса  (см.  рис.  1,  справа).

Используя  для  изменения  массы  шарика  формулы,  приведенные  ранее,  получим  уравнение  движения  в  виде:

.

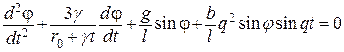Динамика  системы  и  фазовые  портреты  приведены  на  рисунках  11  и  12.

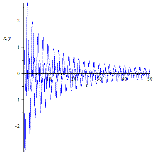
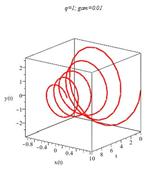
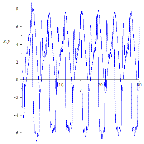
Рисунок  11.  Динамика  маятника  при  растущей  массе  грузика  для  малой  (слева)  и  большой  (справа)  частот  колебаний  точки  подвеса

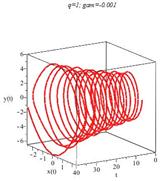
Рисунок  12.  Динамика  маятника  при  убывающей  массе  грузика  для  малой  (слева)  и  большой  (справа)  частот  колебаний  точки  подвеса

Видим,  что  динамика  маятника  при  убывающей  массе  грузика  и  для  малой  и  для  большой  частоте  колебаний  точки  подвеса  подвержена  большей  хаотизации,  чем  при  увеличивающей  массе  грузика.

Видим,  что  рост  частоты  колебаний  точки  подвеса  также  хаотизирует  движение  маятника.

Список  литературы:

1.Бутенин  Н.В.  Теория  колебаний.  М.:  Высшая  школа,  1963.  —  187  с.

2.Рабинович  М.И.,  Трубецков  Д.И.  Введение  в  теорию  колебаний  и  волн.  М.:  Наука,  1984.  —  432  с.

3.Горяченко  В.Д.  Элементы  теории  колебаний.  Учебное  пособие.  Красноярск:  изд-во  Краснояр.  ун-та,  1995.  —  429  с.]

4.Меркин  Д.Р.  Введение  в  теорию  устойчивости  движения.  М.:  Наука,  1987.  —  304  с. 

5.Капица  П.Л.  Динамическая  устойчивость  маятника  при  колеблющейся  точке  подвеса  //  ЖЭТФ,  —  1951,  —  т.  21,  —  вып.  5.

6.Стрелков  С.П.  Введение  в  теорию  колебаний.  М-.Л.:  ГИТТЛ,  1950.  —  344  с.

7.Бать  М.И.,  Джанелидзе  Г.Ю.,  Кельзон  А.С.  Теоретическая  механика  в  примерах  и  задачах.  Т.2.  Динамика.  М.:  Физматлит,  1961.  —  616  с.