О  ДИНАМИЧЕСКИХ  УСЛОВИЯХ  НА  ГРАНИЦАХ  РАЗДЕЛА  СИСТЕМЫ  НЕСМЕШИВАЮЩИХСЯ  КАПИЛЛЯРНЫХ  ВЯЗКИХ  ЖИДКОСТЕЙ

Дудик  Ольга  Александровна

канд.  физ.-мат.  наук,  КИПУ,  РФ,  г.  Симферополь

E -mail:  dudik_tnu@mail.ru

ON  DYNAMICAL  CONDITIONS  ON  THE  BOUNDARIES  OF  THE  SYSTEM  OF  IMMISCIBLE  CAPILLARY  VISCOUS  FLUIDS

Olga  Dudik

candidate  of  physical  and  mathematical  sciences,  Crimean  State  Engineering  and  Pedagogical  University,  Russia,  Simferopol

АННОТАЦИЯ

В  данной  работе  приводится  вывод  динамических  условий  на  границах  раздела  системы  несмешивающихся  однородных  жидкостей,  заполняющих  полость  маятника.  Эти  условия  необходимы  для  полной  математической  постановки  линейных  начально-краевых  задач  гидродинамики.

ABSTRACT

In  this  paper  we  present  dynamical  conditions  on  the  boundaries  of  the  system  of  immiscible  capillary  viscous  fluids  filling  the  cavity  of  the  pendulum.  It  is  necessary  to  provide  the  complete  mathematical  posing  of  linear  initial-boundary  value  problems  of  fluid  dynamics.

Ключевые  слова :  капиллярные  вязкие  жидкости;  динамические  условия.

Keywords :  capillary  viscous  fluids;  dynamical  conditions.

Введение .  Динамические  условия  на  границах  раздела  возникают  в  линейных  задачах  гидродинамики,  связанных  с  движениями  системы  «маятник-вязкие  жидкости»,  в  условиях,  близких  к  невесомости.  Известно,  что  в  условиях  невесомости  или  близких  к  ним  при  рассмотрении  проблемы  колебаний  жидкости,  заполняющей  сосуд,  следует  учитывать  капиллярные  силы,  действующие  на  границах  раздела  «жидкость-газ»,  «жидкость-твердое  тело»,  «газ-твердое  тело».  При  постановке  этих  начально-краевых  проблем  необходимо  учитывать  тот  факт,  что  ввиду  действия  капиллярных  сил  порядок  дифференциального  оператора  на  равновесной  поверхности  жидкости  такой  же,  как  и  в  основных  уравнениях.

Вывод  динамического  условия  на  равновесной  поверхности  жидкости.   Будем  считать,  что  сферический  маятник  с  полостью  ,  частично  заполненной  капиллярной  вязкой  жидкостью,  закреплен  в  некоторой  точке    и  совершает  малые  движения  относительно  этой  точки  под  действием  гравитационных  сил  с  ускорением  ,  а  также  малого  поля  внешних  массовых  сил  .  Считаем,  что  точка    является  началом  неподвижной  декартовой  системы  координат    с  единичными  векторами    вдоль  осей  .

Будем  измерять  отклонения  маятника  от  вертикальной  оси  с  помощью  малого  вектора  углового  перемещения  тела  ,  где    —  орты  подвижной  системы  координат  ,  жестко  связанной  с  маятником.  Если  маятник  находится  в  состоянии  равновесия,  то  оси    и    систем    и    совпадают,  а  давление  в  жидкости  определено  законом  ,  где    —  плотность  жидкости,  .

Пусть  теперь  маятник  отклонен  от  равновесного  положения,  и  это  отклонение  задано  малым  углом  .  Тогда  в  системе  координат    равновесное  давление  ,  с  точностью  до  бесконечно  малых  порядка  ,  равно

           (1)

Обозначим  через  S  часть  границы  области  ,  занятой  жидкостью,  примыкающую  к  твердой  стенке  полости,  а  через    —  свободную  равновесную  поверхность  жидкости.  При  движении  маятника  с  жидким  наполнением  свободная  поверхность  жидкости    будет  отклоняться  от  равновесной  поверхности    на  малую  величину,  и  это  отклонение  будем  измерять  с  помощью  функции  ,  отклонения  вдоль  нормали    к  .  Для  рассмотрения  функций  в  окрестности    введем  криволинейную  ортогональную  систему  координат  с  началом  ,  выбранным  на  ,  такую,  что  уравнение    имеет  вид  ,  а  коэффициент  Ламе    на  .

Запишем  теперь  динамическое  условие  на  движущейся  поверхности    в  криволинейной  системе  координат  .  Если    —  поля  давлений,    —  поля  скоростей  жидкости  в  полости  ,  а    и    —  главные  кривизны  свободной  поверхности  ,  то  скачок  нормальных  напряжений  при  переходе  от  жидкости  к  газу  равен  капиллярному  скачку  давлений  [1,  с.  349],  т.  е.  выполнено  условие

  (2)

где:    —  кинематическая  вязкость  жидкости, 

  —  внешнее  постоянное  давление, 

  —  коэффициент  поверхностного  натяжения  на  границе  «жидкость-газ»,  а  через    обозначены  ковариантные  производные  векторного  поля    по  координате  .

В  состоянии  покоя  на  равновесной  поверхности    выполнено  условие  Лапласа  для  скачка  давлений 

                                     (3)

где:    и  —  главные  кривизны  поверхности  .

Представим    в  жидкости  в  виде 

                          (4)

где:    —  динамическое  давление,  отвечающее  отклоненному  положению  маятника, 

  —  соответствующая  статическая  составляющая.  Воспользуемся  еще  известной  из  геометрии  формулой  для  вариации  кривизны  поверхности

        (5)

где:    —  оператор  Лапласа-Бельтрами;  в  пространственной  задаче  этот  оператор  является  двумерным.

Подставляя  выражение  для    из  (4),    из  (1),    из  (5)  в  условие  (2),  будем  иметь

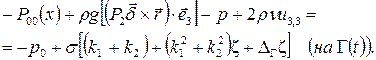           (6)

Представляя  еще 

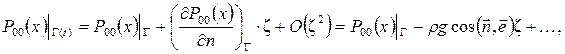из  (6)  с  точностью  до  отброшенных  членов  второго  порядка  малости  получаем:

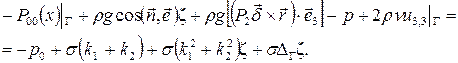             (7)

Так  как  в  состоянии  покоя  на    выполнено  условие  (3),  то,  отбрасывая  в  (7)  члены  нулевого  порядка  малости,  получаем  линеаризованное  динамическое  условие  на  :

              (8)

где

                     (9)

Аналогичным  образом  может  быть  получено  линеаризованное  условие  равенства  нулю  касательных  напряжений  на  :

                    (10)

Условия  (8)—(10)  остаются  справедливыми  не  только  для  пространственной  задачи  (сферический  маятник),  но  и  для  плоской  задачи  (плоский  маятник):

Вывод  динамических  условий  на  границах  раздела  системы  несмешивающихся  жидкостей,  в  условиях  близких  к  невесомости.  Будем  теперь  считать,  что  полость  маятника  заполнена  не  одной  жидкостью,  а  системой  из    несмешивающихся  капиллярных  вязких  жидкостей.  Жидкости  расположены  одна  над  другой  таким  образом,  что  жидкость  наибольшей  плотности    занимает  низшее  (по  отношению  к  действию  ускорения  силы  тяжести  )  положение,  выше  располагается  жидкость,  следующая  по  плотности,  и  т.д.;  иными  словами,  выполнены  неравенства 

Пусть    —  динамические  вязкости  жидкостей;  представим  их  в  виде  ,  где    —  некоторая  средняя  кинематическая  вязкость  системы  жидкостей,  а    имеют  размерности  плотности.  Далее,  при  исследовании  задачи  будем  считать  параметры    фиксированными,  а    —  переменным  параметром. 

В  состоянии  покоя  маятника  с  жидкостями  равновесные  поверхности  между  ними  ,  ,  определены,  а  жидкость  плотности  занимает  область  ,    ограниченную  твердой  стенкой  ,  а  сверху  и  снизу  –  поверхностями    и  ;  при  этом  область    ограничена  только  сверху  границей  раздела  ,  а  область  –  ограничена  только  снизу  границей  раздела  .  Нормали    к  границам    между  -ой  и  -ой  жидкостями  направим  внутрь  -ой  жидкости,  .

Будем  считать,  что  маятник,  закрепленный  в  точке  ,  совершает  малые  движения  относительно  этой  точки.  Обозначим  через  малое  поле  относительной  скорости  жидкости  в  области  ,  а  через    —  соответствующее  динамическое  давление,  т.е.  отклонение  полного  давления    в  области    от  равновесного  давления  ,  отвечающего  состоянию  покоя,  .

На  границах  раздела  должны  выполняться  динамические  условия,  являющиеся  следствием  наличия  капиллярного  скачка  напряжений  при  переходе  из  одной  жидкости  в  другую. 

В  результате  аналогичных  рассуждений,  проведенных  для  случая,  когда  полость  маятника  заполнена  одной  капиллярной  вязкой  жидкостью,  получаем  динамические  условия  на  границах  раздела  системы  несмешивающихся  капиллярных  вязких  жидкостей.  Первая  группа  этих  условий  имеет  вид

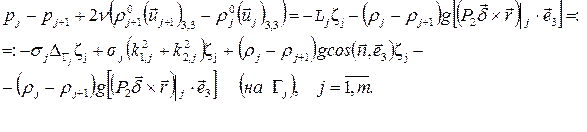
Здесь  —  функции,  заданные  на    и  определяющие  отклонения  вдоль  нормалей    к    возмущенных  движущихся  границ  раздела    от  невозмущенных  (равновесных)  поверхностей  ;  —  коэффициенты  поверхностного  натяжения  на  ;    —  оператор  Лапласа-Бельтрами,  определенный  на  функциях,  заданных  на  ;    и    —  главные  кривизны  поверхности  ;    —  проекции  вектора    на  плоскость  .

Вторая  группа  динамических  условий  выражает  равенство  касательных  напряжений  на  границах  раздела  соседних  жидкостей:

Таким  образом,  динамические  условия  на  границах  раздела  системы  несмешивающихся  капиллярных  вязких  жидкостей  имеют  вид:

Для  плоской  задачи  [2,  с.  73],  учитывая,  что    и    получаем:

Список  литературы:

1.Копачевский  Н.Д.,  Крейн  С.Г.,  Нго  Зуй  Кан.  Операторные  методы  в  линейной  гидродинамике:  Эволюционные  и  спектральные  задачи.  М:  Наука,  1989.  —  416  с.

2.Дудик  О.А.  Малые  движения  и  нормальные  колебания  плоского  маятника  с  полостью,  заполненной  несколькими  капиллярными  вязкими  жидкостями  //  Труды  ИПММ  НАН  Украины.  Донецк:  Инст.  прикл.  мат.  и  мех.  НАН  Украины.  —  2009.  —  Том  19.  —  С.  72—80.

3.Бабский  В.Г.,  Копачевский  Н.Д.,  Мышкис  А.Д.,  Слобожанин  Л.А.,  Тюпцов  А.Д.  Гидромеханика  невесомости.  М:  Наука,  1976.  —  504  с.