СУЩЕСТВОВАНИЕ  И  ЕДИНСТВЕННОСТЬ  РЕШЕНИЯ  ОДНОГО  ИНТЕГРАЛЬНОГО  УРАВНЕНИЯ

Вагапов  Винер  Зуфарович

канд.  физ.-мат.  наук,  доцент  кафедры  математического  анализа  Стерлитамакского  филиала  Башкирского  государственного  университета,  РФ,  Республика,  Башкортостан,  г.  Стерлитамак

E-mail: 

THE  EXISTENCE  AND  UNIQUENESS  OF  THE  SOLUTION  OF  ONE  INTEGRAL  EQUATION

Winer  Vagapov

candidate  of  Science,  assistant  professor  of  the  Sterlitamak  branch  Bashkir  state  university,  Russia,  Republic  of  Bashkortostan,  Sterlitamak

АННОТАЦИЯ

В  статье  при  помощи  специально  подобранного  оператора  показано  решение  одного  интегрального  уравнения  Вольтерра  первого  рода.

ABSTRACT

In  the  article  with  the  help  of  specially  selected  operator  shows  the  solution  of  one  Volterra  integral  equation  of  the  first  kind.

Ключевые  слова:  интегральное  уравнение;  Вольтерра;  оператор.

Keywords:  integral  equation;  Volterra;  operator.

Решение  многих  краевых  задач  для  уравнений  смешанного  типа  сводится  к  решению  интегральных  уравнений,  правые  части  которых  содержат  заданные  граничные  функции.  Рассмотрим  одно  из  таких  интегральных  уравнений, 

    (1)

где:  заданная  достаточно  гладкая  функция, 

  искомая  функция,  ,  .

На  обе  части  уравнения  (1)  подействуем  оператором  .  Будем  иметь

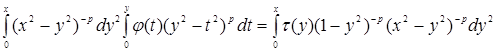  .  (2)

Слева  в  повторном  интеграле  поменяем  порядки  интегрирования: 

.

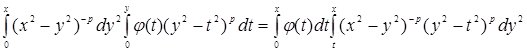Во  внутреннем  интеграле  выполним  замену  переменной:  .  Тогда 

где:    бета-функция. 

С  учетом  этого  уравнение  (2)  принимает  вид: 

  .  (3)

К  интегралу  в  правой  части  уравнения  (3)  применим  метод  интегрирования  по  частям,  полагая  ,  а  в  качестве  функции    возьмем  следующую

или,  учитывая  формулу  интегрального  представления  гипергеометрической  функции  Гаусса  2.12(1)  [1]

,

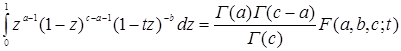где:  гамма-функция,  окончательно  имеем

.

После  применения  метода  интегрирования  по  частям  к  правой  части  уравнения  (3),  где  мы  считаем,  что  ,  приходим  к  следующему  уравнению 

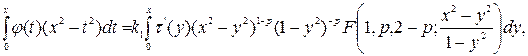
где  .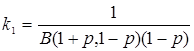

Перепишем  его  в  виде

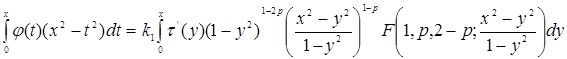
и  продифференцируем  по    обе  части  полученного  уравнения,  применяя  для  производной  от  правой  части  формулу  «сокращенного  дифференцирования»  2.8(22)  [1]

.

Получим  уравнение:

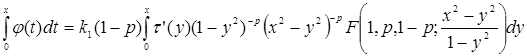  .  (4)

К  гипергеометрической  функции  Гаусса 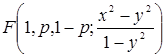   применим  формулу  автотрансформации  2.9(2)  [1]

.

Тогда  уравнение  (4)  перепишется  так: 

  .  (5)

К  интегралу  в  правой  части  этого  уравнения  применим  метод  интегрирования  по  частям,  полагая:

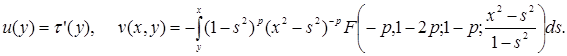
Разложим  гипергеометрическую  функцию  Гаусса  в  степенной  ряд  и  поменяем  порядки  интегрирования  и  суммирования.  Тогда

или  после  выполнения  в  интеграле  замены  переменных  :

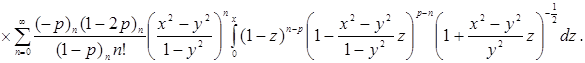
Далее,  используя  формулу  5.8(5)  [1]  интегрального  представления  гипергеометрической  функции  двух  переменных 

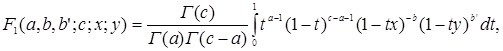
имеем

.

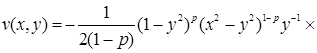
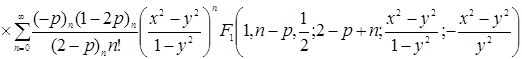Воспользовавшись  формулой  5.7(6)  [1],  представим  функцию    в  виде  двойного  ряда  по    и    и  поменяем  порядки  суммирования  по  и  :

.

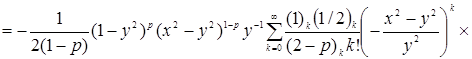
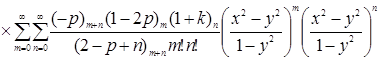Вновь  используя  формулу  5.7(6)  [1],  получим

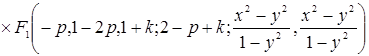
или  в  силу  формулы  5.10(11)  [1] 

имеем

.

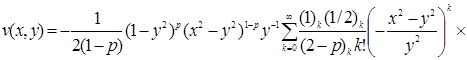
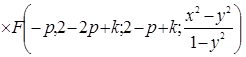Разложим  полученную  гипергеометрическую  функцию  Гаусса  в  ряд  по    и  воспользуемся  представлением  введенной  профессором  Волкодавовым  В.Ф.  гипергеометрической  функции    [2]  в  виде  суммы  двойного  ряда 

.

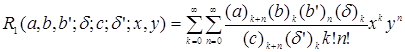Тогда  окончательно  имеем

.

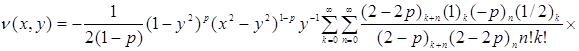
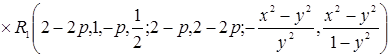После  применения  метода  интегрирования  по  частям,  где  мы  считаем  ,  уравнение  (5)  примет  вид 

.

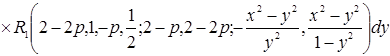Продифференцируем  обе  части  последнего  уравнения,  используя  формулу  (1.4)  [2]

,

где    и    не  зависят  от  .  Окончательно  получим  формулу  обращения  интегрального  уравнения  (1):

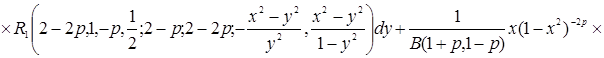
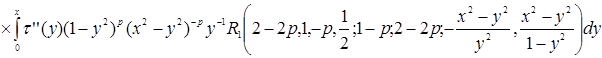.  (6)

Итак,  сформулируем  итоговую  теорему.

Теорема.  Если    ,,  то  интегральное  уравнение  (1)  имеет  единственное  решение,  которое  определяется  формулой  (6).

Список  литературы:

1.Бейтмен  Г.,  Эрдейи  А.  Высшие  трансцендентные  функции.  Т.  1.  Гипергеометрическая  функция.  Функции  Лежандра.  М.:  Наука,  1973.  —  295  с.

2.Волкодавов  В.Ф.,  Николаев  Н.Я.  Интегральные  уравнения  Вольтерра  первого  рода  с  некоторыми  специальными  функциями  в  ядрах  и  их  приложения.  Самара:  Самарский  университет,  1992.  —  100  с.