Статья опубликована в рамках: XIV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 15 января 2014 г.)
Наука: Математика
Секция: Математическая физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
СХОДИМОСТЬ ПЕРВОЙ НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ С НЕЛОКАЛЬНЫМ ЛИНЕЙНЫМ ИСТОЧНИКОМ
Саиег Тимур Хайтам
канд. физ.-мат. наук, доцент кафедры «Высшая Алгебра и Геометрия»,
Северо-Кавказского федерального университта, РФ, г. Ставрополь
E-mail: dr.timor@mail.ru
CONVERGENCE OF FIRST INITIAL BOUNDARY VALUE PROBLEM WITH NONLOCAL LINEAR SOURCE
Timur Haitham Saieg
candidate of Physical and Mathematical Sciences, associate professor of Higher Algebra and Geometry department, North-Caucasus Federal University, Russia Stavropol
АННОТАЦИЯ
Получена априорная оценка для решения первой краевой задачи для уравнения теплопроводности с нелокальным линейным источником, откуда следует сходимости метода Ротэ.
ABSTRACT
There is deduced a prior estimate for the solution of the first boundary value problem for a heat conduction equation with a nonlocal linear source which implies the convergence of Rothe’s method
Ключевые слова: Априорная оценка; метод Ротэ.
Keywords: prior estimate; Rothe’s method.
![]() В области
В области ![]() рассмотрим задачу
рассмотрим задачу
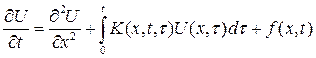 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
где ![]() ,
, ![]() ,
, ![]() — известные достаточно гладкие в
— известные достаточно гладкие в ![]() функции.
функции.
Пусть задача (1)-(3) имеет регулярное решение. Умножим уравнение (1) скалярно на ![]() :
:
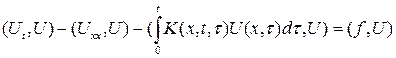 (4)
(4)
Преобразуем каждое слагаемое тождество (4)
![]()
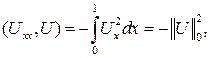
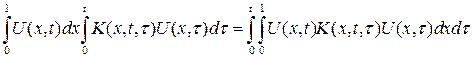
Оценим внутренний интеграл
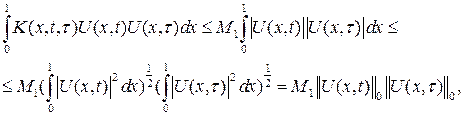
Или
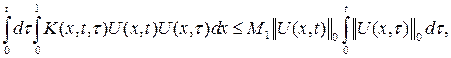
![]()
![]()
Подставляя последние соотношения в тождество (4,) находим
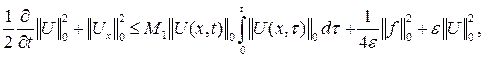
![]() — любое число.
— любое число.
Так как ![]()
То имеем
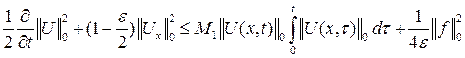 .
.
Пусть ![]() , тогда
, тогда
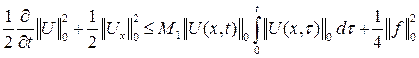 (5)
(5)
Проинтегрируем (5) по τ от 0 до t, тогда получим
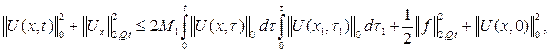 (6)
(6)
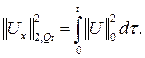
Оценим интегральный член в соотношении (6) таким образом:
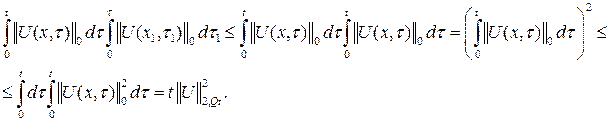
Подставляя последнее в (6), получаем
![]() (7)
(7)
Из (7) имеем
![]()
![]()
или,
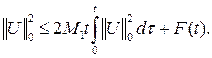 (8)
(8)
При получении априорных оценок решений различных нестационарных задач часто используется следующая
Лемма. Пусть неотрицательная абсолютно непрерывная функция Y(t) удовлетворяет для почти всех ![]() неравенству
неравенству
![]()
где ![]() — суммируемые на [0,T] неотрицательные функции. Тогда
— суммируемые на [0,T] неотрицательные функции. Тогда
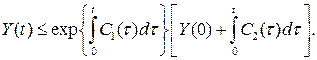
Доказательство леммы приведено в [1].
Применяя к неравенству (8) лемму, получаем
![]()
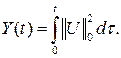
С помощью последней оценки из (7) находим априорную оценку
![]() (9)
(9)
В частности, из оценки (9) следует единственность решения исходной задачи (1)-(3).
Введём на ![]() сетку
сетку ![]()
Задаче (1)-(3) поставим в соотвествие схему Ротэ
![]()
![]()
![]() (10)
(10)
![]()
где ![]() — шаг сетки по времени.
— шаг сетки по времени.
Для доказательства сходимости метода Ротэ, получим дискретный аналог оценки (9). Для чего умножим уравнение (10) скалярно на ![]() .
.
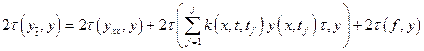 . (11)
. (11)
Преобразуем интегралы, входящие в (11) следующим образом:
![]()
![]()
![]()
![]() (12)
(12)
Оценим интеграл таким образом:
![]()
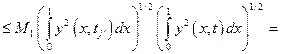
![]() .
.
Стоящую в правой части (12) сумму оценим теперь так:
![]()
![]()
С учётом этих соотношений из тождества (11) получаем
![]()
![]()
Откуда, с учётом неравенства
![]()
Находим
![]()
![]()
Суммируя последнее неравенство по ![]() от 1 до
от 1 до ![]() , получаем
, получаем
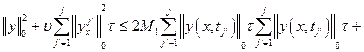
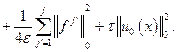
Откуда
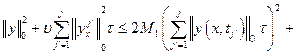
![]()
Или
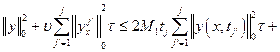
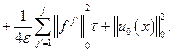 (13)
(13)
Лемма 2. Пусть ![]() функции, заданные на
функции, заданные на ![]() -неотрицательная неубывающая функция
-неотрицательная неубывающая функция ![]() , тогда из неравенства
, тогда из неравенства
![]()
следует
![]()
На основании леммы 2 из (13), при малом ![]() , находим
, находим
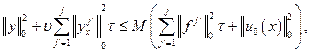 (14)
(14)
где ![]() — постоянная, не зависящая от
— постоянная, не зависящая от ![]() .
.
Обозначим через ![]() , тогда для погрешности я имеем задачу
, тогда для погрешности я имеем задачу
![]()
![]() (15)
(15)
![]()
где ![]() .
.
Применяя оценку (14) к задаче для погрешности (15) находим
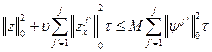
Откуда следует сходимость метода Ротэ со скоростью ![]() .
.
Список литературы:
1.Андреев В.Б. О сходимости разностных схем, аппроксимирующих третью краевые задачи для эллиптических уравнений. Ж. Вычислительная математика и математическая физика. — 1968, — 8 № 6, — с. 1218—1231.
2.Вольтерра В. Математическая теория борьбы за существование. М.: Наука 1976, — 286 с.
3.Кожанов А.И. Параболические уравнения с нелинейным нелокальным источником. сиб. матем. журн., — 1994, — Т. 35, — № 5, — С. 1062—1073.
4.Самарский А.А. теория разностных схем. М.: Наука, 1989. — 616 с.
дипломов


Оставить комментарий