Статья опубликована в рамках: XIV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 15 января 2014 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АНАЛИТИЧЕСКИЕ ФУНКЦИИ ОБОБЩЕННОГО КОМПЛЕКСНОГО ПЕРЕМЕННОГО И НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
Сагиндыков Бимурат Жумабекович
канд. физ.-мат. наук, доцент КазНТУ, Республика Казахстан, г. Алматы
E-mail: bimurat55@gmail.com
Бимурат Жанар
Магистр КазНТУ, Республика Казахстан, г. Алматы
ANALYTICAL FUNCTIONS OF GENERALIZED COMPLEX VARIABLES AND IT’S APPLICATIONS
Bimurat Sagindykov
candidate (PhD) of Physical and Mathematical sciences, KazNTU, Republic of Kazakhstan Almaty
Zhanar Bimurat
Master of Science KazNTU, Republic of Kazakhstan Almaty
Аннотация
Целью данного направления является применение функции обобщенного комплексного переменного к задачам гидродинамики и теории упругости. В этой работе для таких функций получены условия Коши-Римана и соответственно обобщенное уравнение Лапласа. Получена обобщенная формула Пуассона.
abstract
The object of this work is the use of generalized functions of a complex variable to solve the problems of fluid dynamics and elasticity theory. In this paper for this kind of functions we obtained Cauchy-Riemann conditions and, accordingly, the generalized Laplace equation and the generalized Poisson formula.
Ключевые слова: условия Коши-Римана; обобщенное уравнение Лапласа; формула Пуассона.
Keywords: Cauchy-Riemann conditions; generalized Laplace equation; Poisson formula.
Введение
Обобщенные комплексные числа делятся на типы [1]. А именно, различают эллиптические, гиперболические и параболические комплексные числа. Это означает следующее. Пусть ![]() обобщенное комплексное число и
обобщенное комплексное число и ![]() , где
, где ![]() — вещественные числа. Тогда числа делятся на указанные типы в зависимости от того, какими являются
— вещественные числа. Тогда числа делятся на указанные типы в зависимости от того, какими являются ![]() . Если
. Если ![]() , то такие обобщенные комплексные числа относятся к эллиптическому типу, если же
, то такие обобщенные комплексные числа относятся к эллиптическому типу, если же ![]() — то к гиперболическому, если
— то к гиперболическому, если ![]() — параболическому типу.
— параболическому типу.
Если взять ![]() , то мы получим обычные комплексные числа. Если
, то мы получим обычные комплексные числа. Если ![]() , то мы получим двойные числа. Если
, то мы получим двойные числа. Если ![]() , то получим дуальные числа.
, то получим дуальные числа.
В данной работе теория аналитических функций ![]() обобщенного комплексного переменного
обобщенного комплексного переменного ![]() , удовлетворяющих системе уравнений Коши-Римана :
, удовлетворяющих системе уравнений Коши-Римана :
![]() ,
, ![]() , (1)
, (1)
которая по существу эквивалентна уравнению Лапласа
![]() . (2)
. (2)
Аналогично для мнимой части функции ![]() имеем
имеем
![]() . (3)
. (3)
Эквивалентность условий Коши-Римана и условия ![]()
Пусть дана функция ![]() . Переменные
. Переменные ![]() и
и ![]() легко выразить через
легко выразить через ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
где ![]() . Поэтому функцию
. Поэтому функцию ![]() формально можно рассматривать как функцию двух переменных
формально можно рассматривать как функцию двух переменных ![]() и
и ![]() . Найдем
. Найдем ![]() . Для этого рассмотрим дифференциальные операторы
. Для этого рассмотрим дифференциальные операторы
![]() , (4)
, (4)
![]() , (5)
, (5)
которые обладают следующим свойством:
![]() .
.
Поэтому однозначно определены операторы вида
![]() .
.
В частности при ![]() , имеем
, имеем

![]() (6)
(6)
где ![]() .
.
В случае когда ![]() ; обобщенный бигармонический оператор записывается в виде:
; обобщенный бигармонический оператор записывается в виде:
![]() , (7)
, (7)
Отсюда при ![]() как следствие получим обычный бигармонический оператор
как следствие получим обычный бигармонический оператор
![]() .
.
Здесь ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
Теорема. Условия Коши-Римана и ![]() эквивалентны.
эквивалентны.
Если ![]() , то
, то 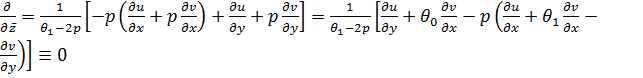 . Отсюда следует справедливость условий Коши-Римана
. Отсюда следует справедливость условий Коши-Римана
![]() ,
,
![]() .
.
В общем случае интеграл![]() , здесь
, здесь ![]() зависит от формы пути. Выясним условия, при которых интеграл от формы пути не зависит. Ответ на этот вопрос содержится в следующий теореме.
зависит от формы пути. Выясним условия, при которых интеграл от формы пути не зависит. Ответ на этот вопрос содержится в следующий теореме.
Теорема Коши. Если функция ![]() обобщенно-аналитическая в односвязной области
обобщенно-аналитическая в односвязной области ![]() , то интеграл от этой функции вдоль всякого замкнутого кусочно-гладкого контура
, то интеграл от этой функции вдоль всякого замкнутого кусочно-гладкого контура ![]() , целиком лежащего в
, целиком лежащего в ![]() , равен нулю.
, равен нулю.
Доказательство. Пусть ![]() — аналитическая в области
— аналитическая в области ![]() функция. Имеем
функция. Имеем

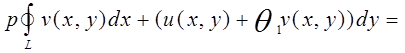

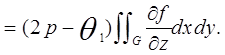
Из условия Коши-Римана следует, что ![]() . Это условие и непрерывности функций
. Это условие и непрерывности функций ![]() достаточно для обращения интегралов в нуль.
достаточно для обращения интегралов в нуль.
Условия Коши-Римана в полярных координатах
От алгебраической формы ![]() обобщенного комплексного числа переходим к его показательно-тригонометрической форме
обобщенного комплексного числа переходим к его показательно-тригонометрической форме
![]() ,
,
где
![]()
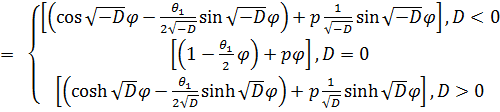 (9)
(9)
В частности при ![]() имеем:
имеем: ![]() ; отсюда получаем формулу Эйлера
; отсюда получаем формулу Эйлера ![]() .
.
Теперь учитывая формулу связи между декартовыми и обобщенно полярными координатами точки на плоскости запишем: ![]() ,
, ![]() , где
, где ![]() .
.
Некоторые вычисления необходимые в дальнейшем. Пусть
![]() .
.
Тогда ![]() и
и ![]() . Из последних двух равенств по формулам вычисления частных производных сложной функции двух переменных находим
. Из последних двух равенств по формулам вычисления частных производных сложной функции двух переменных находим
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Отсюда ![]() ,
, ![]() , где
, где ![]() .
.
Чтобы написать условия Коши-Римана в полярных координатах, вводим следующий дифференциальный оператор
![]() .
.
Тогда условия Коши-Римана можно записать в виде ![]() и оно эквивалентно следующей системе.
и оно эквивалентно следующей системе.
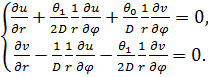 (10)
(10)
В частности имеем при ![]() имеем
имеем ![]() ,
, ![]() .
.
Далее (10) запишем в компактной форме. Для этого систему (10) решим относительно ![]() .
.
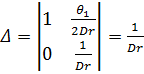 ,
, 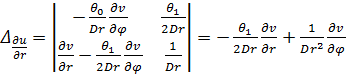 ,
,
 ,
,
![]() ,
, 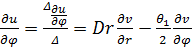 .
.
Аналогично решая систему (10) относительно ![]() . Имеем
. Имеем
![]() ,
, ![]() ,
,
которые по существу эквивалентны уравнению Лапласа записанному в обобщенной полярной системе координат
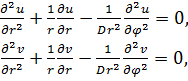 (11)
(11)
где ![]() .
.
Рассмотрим ряд примеров
Пример 1. Функция ![]() , где
, где ![]() — расстояние между точками
— расстояние между точками ![]() и
и ![]() обобщенной плоскости
обобщенной плоскости ![]() , т.е.
, т.е. ![]() является гармонической в любой области обобщенной плоскости
является гармонической в любой области обобщенной плоскости ![]() , не содержащей точку
, не содержащей точку ![]() .
.
Решение. Для удобства вычисления расстояние между точками представим в следующем виде
![]() .
.
Отсюда ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда для функции
. Тогда для функции ![]() , имеем:
, имеем:
![]() ,
,
![]() и
и ![]() .
.
Подставляя найденные значения производных ![]() и
и ![]() в уравнение Лапласа получим
в уравнение Лапласа получим
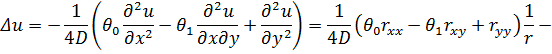
![]() ,
,
во всех точках ![]() обобщенной плоскости
обобщенной плоскости ![]() , за исключением точки
, за исключением точки ![]() , так как
, так как ![]() ,
, ![]() .
.
Таким образом, функция ![]() является решением уравнения Лапласа на обобщенной плоскости
является решением уравнения Лапласа на обобщенной плоскости ![]() за исключением точки
за исключением точки ![]() где она обращается в
где она обращается в ![]() .
.
Пример 2. Решение задачи Дирихле для обобщенного уравнения Лапласа
Рассмотрим внутреннюю краевую задачу для уравнения Лапласа с граничным условием Дирихле

в области ![]() с границей
с границей
![]() ;
;
где ![]() — вещественные управляющие параметры. Здесь
— вещественные управляющие параметры. Здесь
![]() .
.
Задача Дирихле. Найти в области ![]() функцию
функцию ![]() , удовлетворяющую следующим условиям:
, удовлетворяющую следующим условиям:
![]() , (12)
, (12)
![]() ,
, ![]() (13)
(13)
![]() (14)
(14)
где: ![]() — заданная функция; будем считать, что
— заданная функция; будем считать, что ![]() ,
,
![]() .
.
В области ![]() перейдем к обобщенно полярным координатам
перейдем к обобщенно полярным координатам ![]() ,
, ![]() . Тогда уравнение (13) в полярных координатах имеем вид (см. 11)
. Тогда уравнение (13) в полярных координатах имеем вид (см. 11)
![]() . (15)
. (15)
Решение ![]() уравнения (15) будем искать в виде произведения двух функций.
уравнения (15) будем искать в виде произведения двух функций.
![]() в
в ![]() (16)
(16)
Подставляя предполагаемую форму решения (16) в уравнение (15) и разделяя переменные, получим
![]() .
.
Отсюда следует, что функция ![]() должна быть найдена из решения уравнения
должна быть найдена из решения уравнения
![]() , (17)
, (17)
а для функции ![]() получим задачу на собственные значения
получим задачу на собственные значения
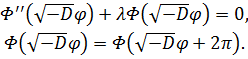 (18)
(18)
Здесь условие периодичности функции ![]() является следствием периодичности искомого решения
является следствием периодичности искомого решения ![]() по угловой переменной с периодом
по угловой переменной с периодом ![]() . Это возможно только в том случае, когда
. Это возможно только в том случае, когда ![]() и когда
и когда ![]() - целое. Тогда общее решение дифференциального уравнения (18) определяется по формуле
- целое. Тогда общее решение дифференциального уравнения (18) определяется по формуле
![]() ,
,
где ![]() и
и ![]() — произвольные постоянные.
— произвольные постоянные.
Уравнение (17) при ![]() имеет два линейно независимых решения
имеет два линейно независимых решения
![]() .
.
где ![]() . Так как частные решения уравнения (17) при
. Так как частные решения уравнения (17) при ![]() ищем в виде степенной функции
ищем в виде степенной функции ![]() . Подставив эту функцию в уравнение (17) установим, что показатель степени
. Подставив эту функцию в уравнение (17) установим, что показатель степени ![]() определяется из уравнения
определяется из уравнения
![]() , т.е.
, т.е. ![]() .
.
Решение внутренней задачи Дирихле должно быть ограничено в рассматриваемой области при ![]() . Поэтому из двух найденных решений следует взять лишь
. Поэтому из двух найденных решений следует взять лишь
![]() .
.
Таким образом, согласно (16) частные решения уравнения (15) можно записать так:
![]() .
.
В силу линейности и однородности уравнения (15) суперпозиция частных решений
![]() , (19)
, (19)
также будет удовлетворять этому уравнению.
Таким образом, ряд (19) внутри области ![]() является гармонической функцией. Из общего курса известно, что ряд (19) сходится равномерно на
является гармонической функцией. Из общего курса известно, что ряд (19) сходится равномерно на ![]() . Тогда удовлетворяя ряд (19) граничному условию (14), получим
. Тогда удовлетворяя ряд (19) граничному условию (14), получим
![]()
или
![]() . (20)
. (20)
Ряд (20) представляет собой разложение в ряд Фурье функции ![]() на промежутке
на промежутке ![]() . Тогда коэффициенты
. Тогда коэффициенты ![]() и
и ![]() определяются по формулам:
определяются по формулам:
![]() , (21)
, (21)
![]() . (22)
. (22)
Теорема. Если функция ![]() и
и ![]() , то существует единственное решение задачи Дирихле в области
, то существует единственное решение задачи Дирихле в области ![]() , которое определяется рядом (19).
, которое определяется рядом (19).
Формула Пуассона
Преобразуем ряд (19) с учетом выражений (21) и (22):
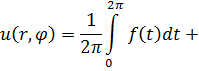
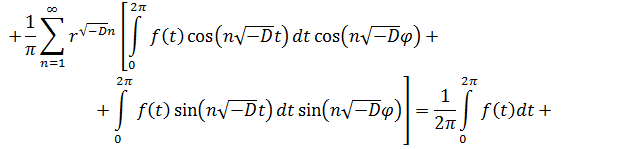

![]()
![]() (23)
(23)
Учитывая обобщенную формулу Эйлера (9), имеем:
![]() .
.
Найдем сумму ряда
![]()
![]()
![]() (24)
(24)
Тогда, подставляя (24) в (23), найдем формулу
![]() , (25)
, (25)
которая называется формулой Пуассона.
Пример 3. Вычислить интеграл ![]() .
.
Решение. в случае, когда ![]() формулу (9) можно записать в виде
формулу (9) можно записать в виде
![]()
![]() . (26)
. (26)
Тогда ![]() . Отсюда
. Отсюда
![]() ,
, ![]() ;
;
так как ![]() и
и ![]() . Последний интеграл можно переписать в виде
. Последний интеграл можно переписать в виде
![]() .
.
Здесь ![]() и
и ![]() . Таким образом
. Таким образом
![]() .
.
Из разложения экспоненты (26), имеем следующее соотношения: ![]() ,
, ![]() . Применим эти соотношения
. Применим эти соотношения
![]() ,
,
![]() .
.
Далее параметры ![]() заменим через параметры
заменим через параметры ![]() и
и ![]() , и имеем:
, и имеем:
![]() .
.
Теперь не трудно вычислить искомый интеграл, используя полученные выше результаты.
Интегрирование по частям приводит к понижению степени ![]() под интегралом.
под интегралом.
Действительно,
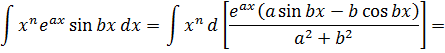
![]() .
.
Список литературы:
- Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их математические модели. М.: Наука, 1973. — 416 с.
- Сагиндыков Б.Ж., Бимурат Жанар. Обобщенная комплексная экспонента и ее применения для отыскания суммы // Естественные и математические науки: вопросы и тенденции развития. 2013. г. Новосибирск, — с. 7—15.
дипломов


Оставить комментарий