Статья опубликована в рамках: XII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 11 ноября 2013 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ДИЗАЙНЕ И АРХИТЕКТУРЕ МАЛЫХ ФОРМ
Мисюра Наталья Евгеньевна
старший преподаватель ИНФО УРФУ, г. Екатеринбург
E-mail: n_misura@mail.ru
Берестова Светлана Александровна
д-р физ.-мат. наук, доцент ИНФО УРФУ, г. Екатеринбург
">
MATHEMATICAL MODELING IN DESIGN AND IN HARD LANDSCAPING
Natalia Musyura
head teacher of Institute of Fundamental Education of Ural Federal University, Ekaterinburg
Svetlana Berestova
doctor of Physical and Mathematical Sciences, associate professor of Institute of Fundamental Education of Ural Federal University, Ekaterinburg
АННОТАЦИЯ
В работе рассмотрены примеры использования математических методов при формообразования элементов декора и малых архитектурных форм. В частности представлены аналитические алгоритмы построения пространственных конструкций сложной конфигурации.
ABSTRACT
The article examines the examples of mathematical methods use when décor and hardscape elements shaping. Namely there are presented analytic space construction algorithms of complicated configuration.
Ключевые слова: математический дизайн; розы Гвидо Гранди; каналовые поверхности; линейчатые поверхности.
Keywords: mathematical design; roses of Guido Grandi; canal surfaces; ruled surfaces.
Появление математического дизайна смело можно связать с именем итальянского монаха Гвидо Гранди (1671—1742). В математике Гранди известен его работой Flores geometrici (1728), изучавшей розы — кривые, которые имеют форму лепестков цветка. Он назвал розы кривой rhodonea и назвал кривую Clelia в честь графини Клелии Борромео.
Уравнение розы Гвидо Гранди в полярных координатах имеет вид
![]() .
.
Задавая параметр ![]() отношением натуральных чисел можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые цветы или в ажурные розетки, которые могут служить элементами декора или орнамента.
отношением натуральных чисел можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые цветы или в ажурные розетки, которые могут служить элементами декора или орнамента.
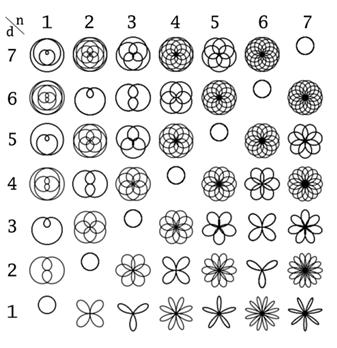
Рисунок 1. Розы Гвидо Гранди [1]
Современные информационные технологии и методы компьютерной геометрии позволяют создавать не только плоские художественные графические формы с использованием тех или иных математических алгоритмов, но и объемные декоративные элементы на основе универсальных математических моделей. К одной из таких моделей может быть отнесена каналовая поверхность [3], уравнение которой записывается в следующем виде:
![]() , (1)
, (1)
где: ![]() — уравнение гладкой регулярной направляющей кривой,
— уравнение гладкой регулярной направляющей кривой,
![]() — единичные векторы нормали и бинормали этой кривой
— единичные векторы нормали и бинормали этой кривой
![]() ,
, ![]() ,
, ![]() . (2)
. (2)
Единичные векторы касательной ![]() , нормали
, нормали ![]() и бинормали
и бинормали ![]() образуют подвижный ортогональный базис, перемещающийся вдоль направляющей кривой.
образуют подвижный ортогональный базис, перемещающийся вдоль направляющей кривой.
В качестве иллюстрации метода построения каналовых поверхностей построим воронку с направляющей кривой в виде параболы
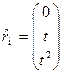 ,
,
В случае, когда функция ![]() задается равенством
задается равенством ![]() .
.
Замечая, что вектор бинормали направлен по оси ![]() , с учетом формул (2)) находим
, с учетом формул (2)) находим
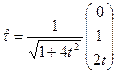 ,
, 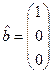 ,
, ![]()
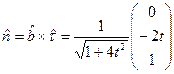
Подстановка этих функций в равенство (1) дает уравнение воронки (рис.2):
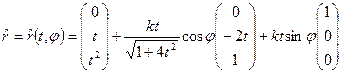 или
или 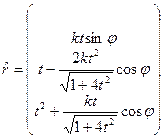 .
.

Рисунок 2. Каналовая поверхность на пароболической направляющей
Рассмотрим процедуру построение тора с направляющей кривой в виде окружности

и эллиптическими сечениями, описываемыми уравнением
![]() .
.
Здесь ![]() и
и ![]() — полуоси эллиптических сечений.
— полуоси эллиптических сечений.
Направление вектора бинормали в данном случае совпадает с осью ![]() , единичные векторы касательной и нормали имеют координаты
, единичные векторы касательной и нормали имеют координаты
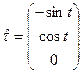 ,
, 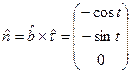
Подстановка этих значений и координат вектора ![]() в уравнение (1) позволяет записать уравнение поверхности тора, изображённого на рис. 3.
в уравнение (1) позволяет записать уравнение поверхности тора, изображённого на рис. 3.

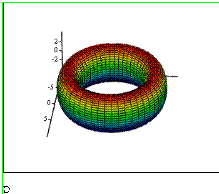
Рисунок 3. Тор с эллиптическим сечением
Рассмотренный алгоритм построения каналовых поверхностей был использован при построении более сложных поверхностей 3D-цветов, представленных на рис. 4. У этих поверхностей направляющей кривой служит винтовая спираль, а в нормальных плоскостях расположены известные плоские кривые, параметры которых изменяются по заданному закону
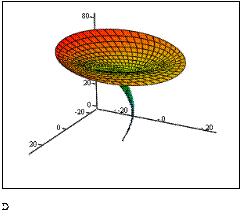

а) Окружность б). Астроида

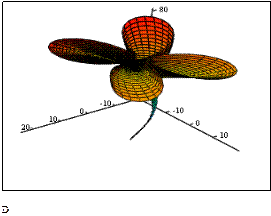
в) Трехлепестковая роза г) Четырехлепестковая роза
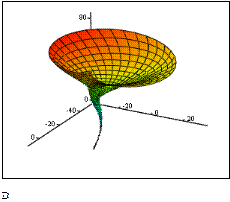
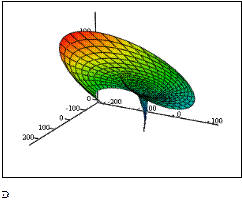
д) Кардиоида е) Спираль Архимеда
![]()
![]() Рисунок 4. 3-D цветы
Рисунок 4. 3-D цветы
В последние годы методы математического моделирования активно используются при создании малых архитектурных форм. Примеры малых архитектурных форм с использованием линейчатых поверхностей [3] представлены на рис. 5.

Рисунок 5. Малые архитектурные формы выполненные с использованием линейчатых поверхностей
В объекты искусства превращаются непосредственно и математические поверхности, примером чего могут служить поверхность Боя и бутылка Клейна. Параметрические уравнения поверхности Боя (рис. 6) имеют вид [2]:

где
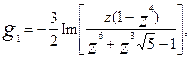
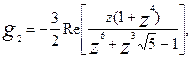
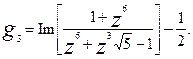

Рисунок 6. Малые архитектурные формы с использованием поверхности Боя
Уравнения поверхности бутылки Клейна ( рис.7) в параметрической форме имеет вид [2] :
![]()
![]()
![]()

Рисунок 7. Дизайнерские объекты выполненные в форме бутылки Клейна
Список литературы:
1.Гвидо Гранди [Электронный ресурс] — Режим доступа. — URL: http://fireshiki.ru/forum/19-578-1 (дата обращения 06.10.2013).
2.Кривошапко С.Н, Иванов В.Н., Халаби С.Н. Аналитические поверхности: материалы по геометрии 500 поверхностей и информация к расчёту на прочность тонких оболочек М: Наука, 2006. — 544 с.
3.Митюшов Е.А., Беляева З.В., Геометрическое моделирование пространственных конструкций Изд.: LAP LAMBERT Academic Publishing, 2011. — 135 с.
дипломов


Комментарии (1)
Оставить комментарий