Статья опубликована в рамках: XII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 11 ноября 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ВНЕШНЯЯ КРАЕВАЯ ЗАДАЧА КАРЛЕМАНА В ДРОБНЫХ ПРОСТРАНСТВАХ БЕСОВА
Альсейтов Амангельды Гумарович
учитель математики, гимназия «Умит», г. Уральск, Казахстан
E-mail: alseyytov@rambler
CARLEMAN BOUNDARY VALUE PROBLEM IN FRACTIONAL BESSOV SPACE
Amangeldy Alseytov
Math teacher, gymnasium “Umit”, Uralsk, Kazakhstan
АННОТАЦИЯ
Настоящая работа посвящена исследованию внешней краевой задачи Карлемана в дробных пространствах Бесова, вложенных в пространство непрерывных функций, но не вложенных в класс непрерывных по Гёльдеру функций. Получено полное решение задачи методом интегральных уравнений с применением свойств интеграла типа Коши по замкнутому ляпуновскому контуру и теорем вложения.
ABSTRACT
This work is devoted to the study of Carleman boundary value problem in fractional Bessov space imbedded into space of continuous functions but not embedded into category of Holder-continuous functions. A complete solution by an integral equation method has been deduced using integral of Cauchy type properties according to a closed Lyapunov contour and embedding theorems.
Ключевые слова: краевая задача Карлемана; сингулярное интегральное уравнение; интеграл типа Коши; вполне непрерывный оператор; дробное пространство; метод интегральных уравнений.
Keywords: Carleman boundary value problem; singular integral equation; integral of Cauchy type; completely continuous operator; fractional space; integral equation method.
Введение. Теория непрерывных краевых задач со сдвигом в классической постановке имеется в монографиях Ф.Д. Гахова [7], Н.И. Мусхелишвили [17] и Г.С. Литвинчука [13].
Полное решение краевой задачи Газемана, а также четырех других основных краевых задач со сдвигом, кроме задачи типа задачи Карлемана, было дано Д.А. Квеселава в 1946—1948 гг. методом интегральных уравнений. Результаты исследований Д.А. Квеселава опубликованы в статьях [9—12]. Указанные работы Д.А. Квеселава сыграли решающую роль в дальнейшем развитии исследований по теории краевых задач и сингулярных интегральных уравнений со сдвигом.
В 1958 г. Г.Ф. Манджавидзе и Б.В. Хведелидзе [15] доказали теорему склеивания и установили конформную эквивалентность краевой задачи Газемана краевой задаче Римана. При этом в работе [15] было использовано дополнительное условие: существование второй производной сдвига ![]() , удовлетворяющей условию Гельдера. В 1964 г. И.Б. Симоненко [18] дал новое обоснование конформной эквивалентности краевой задачи Газемана краевой задаче Римана, свободное от указанного выше дополнительного ограничения.
, удовлетворяющей условию Гельдера. В 1964 г. И.Б. Симоненко [18] дал новое обоснование конформной эквивалентности краевой задачи Газемана краевой задаче Римана, свободное от указанного выше дополнительного ограничения.
Проблема распространения результатов работ [11], [12] и [14] на случай многосвязной области привела В.А. Чернецкого [21], [22] к обоснованию комбинированного метода интегральных уравнений и конформного склеивания, который был впоследствии применен в монографии [13]. Центральное место в этом методе занимает, так называемая, теорема конформного склеивания [13, с. 149]. Первое доказательство этой теоремы для случая аналитического сдвига ![]() , заданного на единичной окружности, дали с помощью вариационного метода теории однолистных функций М. Шеффер и Д. Спенсер [25] [8]. Теорию задачи Карлемана для доказательства отмеченной теоремы первым применил Юн Эр-Цзянь [26]. Ему удалось снять требование аналитичности
, заданного на единичной окружности, дали с помощью вариационного метода теории однолистных функций М. Шеффер и Д. Спенсер [25] [8]. Теорию задачи Карлемана для доказательства отмеченной теоремы первым применил Юн Эр-Цзянь [26]. Ему удалось снять требование аналитичности ![]() и заменить это требование обычным условием существования у функции сдвига
и заменить это требование обычным условием существования у функции сдвига ![]() отличной от нуля гельдеровской производной первого порядка. Полное обоснование доказанной теоремы дано В.А. Чернецким [21], [22]. В этих работах обобщены и уточнены результаты Юн Эр-Цзяня и установлена конформная эквивалентность задачи Карлемана на
отличной от нуля гельдеровской производной первого порядка. Полное обоснование доказанной теоремы дано В.А. Чернецким [21], [22]. В этих работах обобщены и уточнены результаты Юн Эр-Цзяня и установлена конформная эквивалентность задачи Карлемана на ![]() задаче Римана на разомкнутом контуре
задаче Римана на разомкнутом контуре ![]() . Последний результат независимо от В.А. Чернецкого был получен также Л.И. Чибриковой в работе [23].
. Последний результат независимо от В.А. Чернецкого был получен также Л.И. Чибриковой в работе [23].
Различные обобщения краевых задач со сдвигом в направлении расширения классов искомых и заданных функций и контуров можно найти в работах [1], [16], [19], [20], [24].
В основе исследования основных, а также других краевых задач со сдвигом в классическом случае лежит метод конформного склеивания, описанный в [7]. В результате конформного отображения краевая задача со сдвигом сводится к краевой задаче без сдвига, в частности, краевая задача Газемана сводится к краевой задаче Римана. С помощью метода конформного склеивания удается получить числа решений и условий разрешимости указанных задач, либо точные оценки для этих чисел. Хотя метод склеивания является наиболее экономным способом построения качественной теории основных краевых задач со сдвигом на плоскости, эта же цель может быть достигнута также применением метода интегральных уравнений. Этим, однако, не исчерпывается значение последнего метода. Этот метод дает также алгоритмы для нахождения решений и условий разрешимости краевых задач. По этой причине для решения задач Газемана и Карлемана мы будем следовать методу интегральных уравнений, предложенному Д.А. Квеселава [9]. Второй и основной причиной применения нами метода интегральных уравнений при решении указанных выше задач в дробных пространствах является тот факт, что при конформном отображении областей ![]() и
и ![]() на некоторые области ∆+ и ∆-, на которые плоскость разделяется контуром
на некоторые области ∆+ и ∆-, на которые плоскость разделяется контуром ![]() , являющегося образом исходного контура
, являющегося образом исходного контура ![]() , новый контур не является контуром Ляпунова. К настоящему моменту задача Римана в дробных пространствах Бесова решена лишь для случая, когда контур является замкнутым контуром Ляпунова. В случае же внешней краевой задачи Карлемана в дробных пространствах при конформном отображении область
, новый контур не является контуром Ляпунова. К настоящему моменту задача Римана в дробных пространствах Бесова решена лишь для случая, когда контур является замкнутым контуром Ляпунова. В случае же внешней краевой задачи Карлемана в дробных пространствах при конформном отображении область ![]() переходит на плоскость ∆ с разрезом вдоль простой разомкнутой дуги
переходит на плоскость ∆ с разрезом вдоль простой разомкнутой дуги ![]() ; насколько нам известно, задача Римана для разомкнутого контура в дробных пространствах до сих пор не рассмотрена. Отметим, что краевая задача Газемана, которая по-другому называется краевой задачей Римана со сдвигом, полностью решена нами в дробных пространствах Бесова методом интегральных уравнений [2].
; насколько нам известно, задача Римана для разомкнутого контура в дробных пространствах до сих пор не рассмотрена. Отметим, что краевая задача Газемана, которая по-другому называется краевой задачей Римана со сдвигом, полностью решена нами в дробных пространствах Бесова методом интегральных уравнений [2].
В настоящей работе рассмотрим внешнюю краевую задачу Карлемана в дробных пространствах Бесова (определения этих пространств см., напр. [5]) и для удобства приведем без доказательства следующие результаты, которыми часто будем пользоваться в дальнейшем.
Лемма А [5, с. 353]. Пусть ![]() и замыкание
и замыкание ![]() ограниченной области
ограниченной области ![]() пространства
пространства ![]() точек
точек ![]() взаимно однозначно отображается на замыкание
взаимно однозначно отображается на замыкание ![]() области
области ![]() пространства
пространства ![]() точек
точек ![]() при помощи отображения
при помощи отображения ![]() , определяемого функциями
, определяемого функциями
![]()
принадлежащими классам ![]() , где
, где
![]() при нецелом
при нецелом ![]() ,
,
![]() при целом
при целом ![]() , (А1)
, (А1)
С якобианом

где 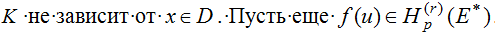 .
.
Тогда:
1. Функция ![]() oт
oт ![]() интегрируема в
интегрируема в ![]() -й степени на
-й степени на ![]() (при
(при ![]() ограничена) и имеет частные производные по
ограничена) и имеет частные производные по ![]() порядков
порядков ![]() , вычисляемые почти всюду на
, вычисляемые почти всюду на ![]() по тем же правилам, как если бы
по тем же правилам, как если бы ![]() имела непрерывные частные производные по
имела непрерывные частные производные по ![]() .
.
При этом
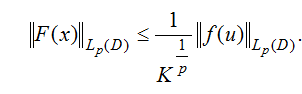
2. Функция ![]() и
и

где: ![]() — константа, зависящая от
— константа, зависящая от ![]() , полунормы
, полунормы ![]() и
и ![]() ,
,
![]() — число, определяемое в (А1).
— число, определяемое в (А1).
В этом утверждении можно всюду заменить ![]() на
на ![]() (
(![]() ), однако в предложении, что
), однако в предложении, что ![]() , где (вместо (А1))
, где (вместо (А1))
![]() ,
, ![]() .
.
Лемма В [6, с. 61]. Пусть ![]() ,
, ![]() ,
, ![]() , где
, где ![]() удовлетворяют одному из условий a)—c):
удовлетворяют одному из условий a)—c):

Пусть выполнено условие  . Тогда интеграл типа Коши
. Тогда интеграл типа Коши
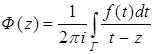 (В1)
(В1)
принадлежит пространству ![]() ,
, 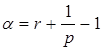
и
![]() ,
,
где постоянная ![]() не зависит от
не зависит от ![]() .
.
Следствие В.1. В условиях леммы интеграл типа Коши (В1) имеет граничные значения слева ![]() и справа
и справа ![]()
![]() , принадлежащие
, принадлежащие ![]() , причем
, причем
![]() ,
,
где постоянная ![]() не зависит от
не зависит от ![]() . Из этого, в частности, следует справедливость формул Сохоцкого-Племеля.
. Из этого, в частности, следует справедливость формул Сохоцкого-Племеля.
Следствие В.2. В условиях леммы сингулярный оператор
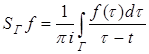 ,
, ![]()
понимаемый в смысле главного значения по Коши, ограничен в ![]() ,
,
![]() ,
,
где постоянная ![]() не зависит от
не зависит от ![]() .
.
Для рассматриваемых нами пространств имеют место вложения

2. Постановка задачи. Пусть ![]() — простой гладкий замкнутый контур класса Ляпунова
— простой гладкий замкнутый контур класса Ляпунова ![]() ,
, 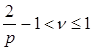 ,
, ![]() и разбивает плоскость комплексного переменного на две области: внутреннюю
и разбивает плоскость комплексного переменного на две области: внутреннюю ![]() , содержащую начало координат, и внешнюю
, содержащую начало координат, и внешнюю ![]() , содержащую бесконечно удаленную точку. Требуется определить функцию
, содержащую бесконечно удаленную точку. Требуется определить функцию ![]() , аналитическую в
, аналитическую в ![]() , удовлетворяющую на контуре
, удовлетворяющую на контуре ![]() краевому условию
краевому условию
![]() , (1)
, (1)
где ![]() и
и ![]() — заданные на контуре
— заданные на контуре ![]() функции класса Бесова
функции класса Бесова ![]() ,
,![]() , причем
, причем ![]() всюду на
всюду на ![]() . Функция
. Функция ![]() переводит контур
переводит контур ![]() взаимно однозначно в себя с изменением направления в нем, а также имеет производную
взаимно однозначно в себя с изменением направления в нем, а также имеет производную  ,
, ![]() , отличную от нуля в точках
, отличную от нуля в точках ![]() . Предполагаем, что выполняется условие Карлемана
. Предполагаем, что выполняется условие Карлемана
![]() . (2)
. (2)
Как увидим ниже, краевое значение ![]() искомой аналитической функции также принадлежит
искомой аналитической функции также принадлежит 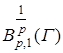 ,
, ![]() . Из
. Из  следует, что
следует, что  . Тогда согласно лемме А
. Тогда согласно лемме А  ,
, ![]() .
.
Заменяя в краевом условии (1) ![]() на
на ![]() , получим в силу условия (2)
, получим в силу условия (2)
![]() . (3)
. (3)
По лемме А ![]() и
и ![]() принадлежат
принадлежат 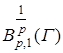 ,
, ![]() . Исключая из (1) и (3) предельное значение
. Исключая из (1) и (3) предельное значение ![]() , получим
, получим
![]() . (4)
. (4)
Соотношение (4) будет удовлетворяться в двух случаях:
1) Выражение 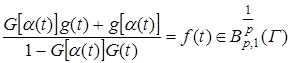 ,
, ![]() , есть краевое значение аналитической в
, есть краевое значение аналитической в ![]() функции. В этом случае искомая функция определится по своему краевому значению интегралом Коши
функции. В этом случае искомая функция определится по своему краевому значению интегралом Коши
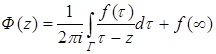
и по лемме В  .
.
2) Соотношение (4) вырождается в тождество. Следовательно,

В дальнейшем будем решать задачу (1) в предположении, что условия (5) и (6) выполнены.
Заметим, что функции
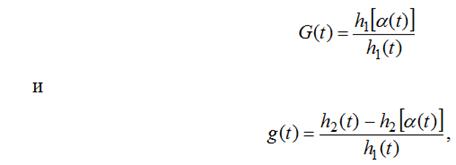
где ![]() и
и ![]() — любые функции из
— любые функции из 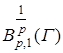 ,
, ![]() , причем
, причем ![]() , удовлетворяют условиям (5) и (6). Действительно, по лемме А
, удовлетворяют условиям (5) и (6). Действительно, по лемме А  ,
, ![]() ,
, ![]() , и в силу этого и условия (2)
, и в силу этого и условия (2)
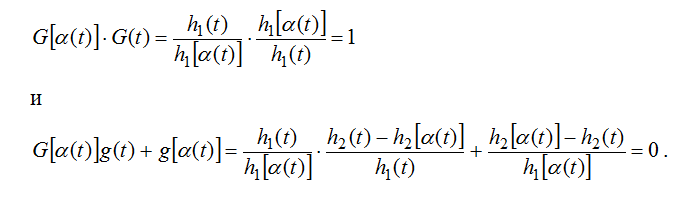
3. Интегральные представления. Рассмотрим сначала тот случай, когда краевое условие (1) имеет вид
![]() ,
, ![]() . (7)
. (7)
Из условия (2) следует, что для разрешимости краевой задачи (7) необходимо, чтобы
![]() .
.
Аналитическое в ![]() решение задачи (7) будем искать в виде
решение задачи (7) будем искать в виде
 , (8)
, (8)
где: ![]() — функция из класса
— функция из класса 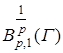 ,
, ![]() , причем
, причем
![]() , (9)
, (9)
где: ![]() — произвольная постоянная. Учитывая условие (9), по формулам Сохоцкого-Племеля, справедливость которых в классах Бесова доказана Н.К. Блиевым [6, с. 64], из (8) будем иметь:
— произвольная постоянная. Учитывая условие (9), по формулам Сохоцкого-Племеля, справедливость которых в классах Бесова доказана Н.К. Блиевым [6, с. 64], из (8) будем иметь:

Приведем соответствующие выкладки:
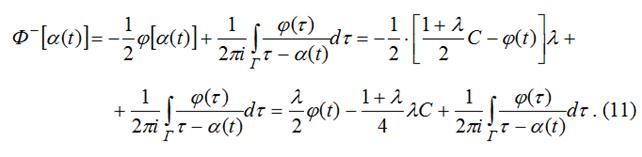
В последнем интеграле сделаем подстановку ![]() , затем переменную
, затем переменную ![]() снова обозначим
снова обозначим ![]() . Учитывая, что сдвиг меняет направление на контуре, а также условие (9), имеем:
. Учитывая, что сдвиг меняет направление на контуре, а также условие (9), имеем:

Последний интеграл существует в смысле главного значения по Коши и равен ![]() . В самом деле, учитывая, что контур интегрирования, во всяком случае, гладкий, и сдвиг меняет направление на
. В самом деле, учитывая, что контур интегрирования, во всяком случае, гладкий, и сдвиг меняет направление на ![]() , получим:
, получим:
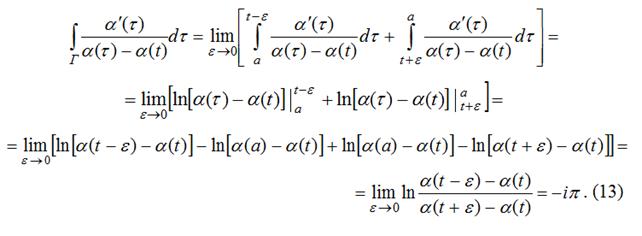
(см. также [7, с. 29]). Объединив (11), (12) и (13) получим второе из равенств (10).
Подставляя (10) в краевое условие (7), получим интегральное уравнение

Интегральный оператор ![]() вполне непрерывен в
вполне непрерывен в 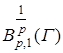 ,
, ![]() [2], [3], [4], т. е. ядро
[2], [3], [4], т. е. ядро ![]() может быть представлено в виде отношения
может быть представлено в виде отношения  . Следовательно, уравнение (14) есть уравнение Фредгольма.
. Следовательно, уравнение (14) есть уравнение Фредгольма.
Лемма 1. Однородное уравнение ![]() имеет своим нетривиальным решением только произвольную постоянную.
имеет своим нетривиальным решением только произвольную постоянную.
Доказательство. Пусть ![]() функция обратная
функция обратная ![]() . Легко показать, что свойства
. Легко показать, что свойства ![]() аналогичны свойствам
аналогичны свойствам ![]() . Произвольная постоянная удовлетворяет уравнению
. Произвольная постоянная удовлетворяет уравнению ![]() . Действительно, пусть
. Действительно, пусть ![]() . Тогда
. Тогда ![]() примет вид
примет вид
![]() .
.
В самом деле, учитывая (13) имеем:
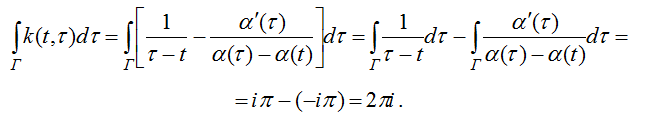
Пусть теперь ![]() — произвольное решение интегрального уравнения
— произвольное решение интегрального уравнения ![]() . Построим две функции
. Построим две функции ![]() и
и ![]() , аналитические в
, аналитические в ![]() :
:

где ![]() функция, обратная к функции сдвига
функция, обратная к функции сдвига ![]() ,
,  по лемме А, а
по лемме А, а ![]() и
и ![]() согласно лемме В принадлежат пространству
согласно лемме В принадлежат пространству 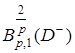 .
.
Используя формул Сохоцкого-Племеля, будем иметь:
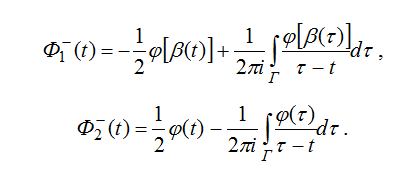
Отсюда сначала с помощью замены переменной интегрирования ![]() и переобозначив
и переобозначив ![]() через
через ![]() , а также учитывая, что
, а также учитывая, что ![]() обратный гомеоморфизм контура
обратный гомеоморфизм контура ![]() на себя и
на себя и ![]() функция, обратная к функции сдвига
функция, обратная к функции сдвига ![]() , получим
, получим
 .
.
Далее рассмотрим разность

и увидим, что
![]()
![]()
в силу интегрального уравнения ![]() . Это означает, что функции
. Это означает, что функции ![]() и
и ![]() удовлетворяют на
удовлетворяют на ![]() краевому условию
краевому условию
![]()
![]() . (15)
. (15)
Из работы [10] известно, что если аналитическое в ![]() функции
функции ![]() и
и ![]() удовлетворяют краевому условию (15), то
удовлетворяют краевому условию (15), то ![]()
![]() . Учитывая, что ввиду представимости интегралами типа Коши функции
. Учитывая, что ввиду представимости интегралами типа Коши функции ![]() и
и ![]() исчезают в бесконечно удаленной точке, отсюда получаем
исчезают в бесконечно удаленной точке, отсюда получаем ![]()
![]() .
.
Таким образом, функции ![]() и
и ![]() являются краевыми значениями некоторых функции
являются краевыми значениями некоторых функции ![]() и
и ![]() аналитических в области
аналитических в области ![]() , т. е.
, т. е.
![]() ,
, ![]() . (16)
. (16)
Из (16) получаем краевое условие на ![]() :
: ![]() .
.
Следовательно, в области ![]() выполняются следующие равенства
выполняются следующие равенства ![]() и
и ![]() [10]. Таким образом, уравнение
[10]. Таким образом, уравнение ![]() имеет лишь одно независимое решение и как показано выше оно есть постоянная. Лемма 1 доказана.
имеет лишь одно независимое решение и как показано выше оно есть постоянная. Лемма 1 доказана.
Следовательно, союзное однородное уравнение ![]() также имеет единственное независимое решение
также имеет единственное независимое решение ![]() , а для разрешимости неоднородного интегрального уравнения
, а для разрешимости неоднородного интегрального уравнения ![]() должно выполняться одно условие разрешимости
должно выполняться одно условие разрешимости
![]() , (17)
, (17)
где ![]() — нетривиальное решение однородного уравнения
— нетривиальное решение однородного уравнения
 . (18)
. (18)
Лемма 2. Если ![]() есть нетривиальное решение уравнения (18), то функция
есть нетривиальное решение уравнения (18), то функция
![]() (19)
(19)
тоже является решением этого уравнения при любой постоянной ![]() .
.
Доказательство. Если ![]() , т. е.,
, т. е., ![]() , то лемма тривиальна. Пусть теперь
, то лемма тривиальна. Пусть теперь ![]() , тогда поступаем следующим образом: перепишем (18) в виде
, тогда поступаем следующим образом: перепишем (18) в виде
 ,
,
затем, заменив ![]() на
на ![]() и умножив на
и умножив на ![]() , имеем
, имеем
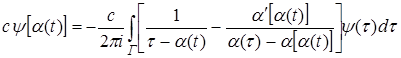
или с учетом условия (2) и следующего из него равенства
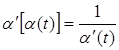 (20)
(20)
получим
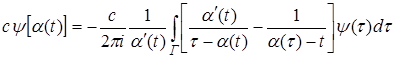 .
.
Совершив в последнем интеграле подстановку ![]() и переобозначив
и переобозначив ![]() через
через ![]() будем иметь
будем иметь
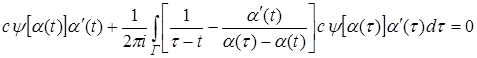 ,
,
что и доказывает лемму.
Лемма 3. Если ![]() — сдвиг Карлемана, то любое решение союзного интегрального уравнения Фредгольма (18) удовлетворяет условию
— сдвиг Карлемана, то любое решение союзного интегрального уравнения Фредгольма (18) удовлетворяет условию
 . (21)
. (21)
Доказательство. В силу того, что уравнение (18) имеет единственную собственную функцию, заключаем ![]() , где
, где ![]() — некоторая постоянная. Полагая
— некоторая постоянная. Полагая ![]() из (19) получим
из (19) получим
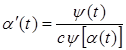 . (22)
. (22)
Изменяющий ориентацию гомеоморфизм ![]() обязательно имеет две неподвижные точки первой кратности, т.е. существуют точки
обязательно имеет две неподвижные точки первой кратности, т.е. существуют точки ![]() такие, что
такие, что ![]() ,
, ![]() . Из (20) следует, что в неподвижных точках
. Из (20) следует, что в неподвижных точках ![]() . Так как
. Так как ![]() изменяет ориентацию на
изменяет ориентацию на ![]() , то
, то ![]() ,
, ![]() . Тогда из (22) имеем
. Тогда из (22) имеем ![]() , отсюда
, отсюда ![]() .
.
Таким образом, показано, что любое решение союзного однородного уравнения (18) удовлетворяет условию (21). Лемма 3 доказана.
Согласно альтернативе Фредгольма неоднородное интегральное уравнение ![]() , где
, где ![]() — некоторая постоянная, не имеет нетривиального решения, отсюда следует, что любое решение союзного однородного уравнения (18) удовлетворяет условию
— некоторая постоянная, не имеет нетривиального решения, отсюда следует, что любое решение союзного однородного уравнения (18) удовлетворяет условию
![]() .
.
Лемма 4. Если
![]() , (23)
, (23)
то интегральное уравнение ![]() разрешимо и любое его решение удовлетворяет условию
разрешимо и любое его решение удовлетворяет условию
![]() , (24)
, (24)
где: ![]() — постоянная.
— постоянная.
Доказательство. В силу условия (23) можно записать
![]() , (25)
, (25)
где: ![]() — любое нетривиальное решение союзного уравнения (18). Перепишем (25) в виде
— любое нетривиальное решение союзного уравнения (18). Перепишем (25) в виде
![]() .
.
Преобразуя интеграл в правой части последнего равенства с помощью замены ![]() , имеем
, имеем
![]() .
.
В силу леммы 3 имеем, что ![]() , и получаем что условие (17) разрешимости уравнения
, и получаем что условие (17) разрешимости уравнения ![]() выполнено. Пусть
выполнено. Пусть ![]() — решение этого уравнения. Тогда функция
— решение этого уравнения. Тогда функция ![]() также является решением. Доказательство последнего утверждения проводится аналогично доказательству леммы 1 с помощью условия (23). Заметим, что функция
также является решением. Доказательство последнего утверждения проводится аналогично доказательству леммы 1 с помощью условия (23). Заметим, что функция ![]() есть решение однородного уравнения
есть решение однородного уравнения ![]() . Но общим решением этого уравнения в силу леммы 1 является произвольная постоянная. Отсюда следует справедливость соотношения (24). Лемма 4 доказана.
. Но общим решением этого уравнения в силу леммы 1 является произвольная постоянная. Отсюда следует справедливость соотношения (24). Лемма 4 доказана.
Из леммы 4 следует справедливость следующего интегрального представления.
Теорема 1. Всякая функция ![]() , аналитическая в области
, аналитическая в области ![]() и имеющая на
и имеющая на ![]() предельные значения
предельные значения  , допускает интегральное представление
, допускает интегральное представление
 , (26)
, (26)
где постоянная ![]() однозначно определяется по
однозначно определяется по ![]() , а плотность
, а плотность ![]() определяется по
определяется по ![]() с точностью до произвольного постоянного слагаемого, причем
с точностью до произвольного постоянного слагаемого, причем ![]() ,
, ![]() — постоянная.
— постоянная.
Доказательство. Так как функция ![]() удовлетворяет условию (23), то согласно лемме 4, уравнение
удовлетворяет условию (23), то согласно лемме 4, уравнение ![]() разрешимо и любое его решение удовлетворяет условию (24). Пусть
разрешимо и любое его решение удовлетворяет условию (24). Пусть ![]() — некоторое решение уравнения
— некоторое решение уравнения
![]() .
.
Введем функцию
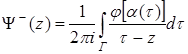 .
.
Учитывая (24), рассмотрим разность
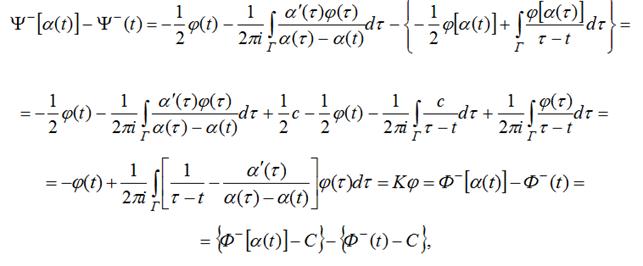
где ![]() .
.
Отсюда имеем
![]() .
.
В силу леммы [10]
![]() , т.е.
, т.е. ![]() . Теорема 1 доказана.
. Теорема 1 доказана.
4. Простейшие неоднородные краевые задачи
Карлемана. На теореме 1 непосредственно основывается решение внешней краевой задачи Карлемана по скачку. Именно, справедлива
Теорема 2. Краевая задача
![]() , (27)
, (27)
где ![]() , разрешима и её общее решение в классе функций, ограниченных на бесконечности, выражается формулой
, разрешима и её общее решение в классе функций, ограниченных на бесконечности, выражается формулой
 ,
,
где: ![]() — решение интегрального уравнения Фредгольма
— решение интегрального уравнения Фредгольма ![]() ,
,
C — произвольная постоянная.
Доказательство. В соответствии с теоремой 1 решение задачи (27) будем искать в виде (26), где плотность ![]() удовлетворяет условию (24). Вычисляя предельные значения
удовлетворяет условию (24). Вычисляя предельные значения ![]() и
и ![]() , и учитывая условие (24), краевую задачу (27) сводим к интегральному уравнению Фредгольма
, и учитывая условие (24), краевую задачу (27) сводим к интегральному уравнению Фредгольма ![]() . В силу условия (23) последнее уравнение, во-первых, разрешимо по лемме 4, а во-вторых, решение этого уравнения удовлетворяет условию (24) и определяется с точностью до произвольной постоянной. Так как эта постоянная в выражение входит в виде слагаемого, то решение
. В силу условия (23) последнее уравнение, во-первых, разрешимо по лемме 4, а во-вторых, решение этого уравнения удовлетворяет условию (24) и определяется с точностью до произвольной постоянной. Так как эта постоянная в выражение входит в виде слагаемого, то решение ![]() на самом деле не зависит от этой постоянной. В качестве
на самом деле не зависит от этой постоянной. В качестве ![]() можем взять любое частное решение уравнения
можем взять любое частное решение уравнения ![]() . Теорема 2 доказана.
. Теорема 2 доказана.
Далее найдем ещё решение краевой задачи
![]() , (28)
, (28)
что соответствует задаче (7) при ![]() , где
, где  ,
, ![]() и удовлетворяет тождеству
и удовлетворяет тождеству
![]() . (29)
. (29)
Теорема 3. Пусть ![]() — обратный сдвиг Карлемана. Всякая функция
— обратный сдвиг Карлемана. Всякая функция ![]() , аналитическая в области
, аналитическая в области ![]() и имеющая всюду на
и имеющая всюду на ![]() предельные значения
предельные значения  ,
, ![]() , допускает интегральное представление
, допускает интегральное представление
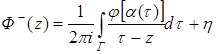 ,
,
где плотность ![]() и постоянная
и постоянная ![]() определяются заданной функцией
определяются заданной функцией ![]() , причем
, причем ![]() удовлетворяет условию
удовлетворяет условию
![]() . (30)
. (30)
Доказательство. Рассмотрим интегральное уравнение
![]() . (31)
. (31)
Необходимое и достаточно условие разрешимости уравнения (31) имеет вид
![]() , (32)
, (32)
где ![]() — любое решение союзного однородного уравнения (18). В силу того, что
— любое решение союзного однородного уравнения (18). В силу того, что ![]() для любого отличного от нулевого решения уравнения (18), мы можем путем подбора постоянной
для любого отличного от нулевого решения уравнения (18), мы можем путем подбора постоянной ![]() сделать выполненным (32).
сделать выполненным (32).
Функция ![]() удовлетворяет условию (29). В силу этого решение уравнения (31) удовлетворяет условию (30). Пусть
удовлетворяет условию (29). В силу этого решение уравнения (31) удовлетворяет условию (30). Пусть ![]() — решение уравнения (31). В силу (30) предельные значения функции
— решение уравнения (31). В силу (30) предельные значения функции
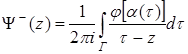
удовлетворяют условию
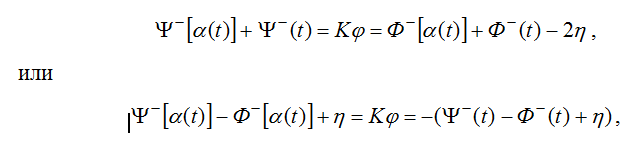
откуда, согласно лемме из [10], имеем
![]() ,
,
что равносильно
![]() .
.
Теорема 3 доказана.
С помощью теоремы 3 докажем теорему о разрешимости краевой задачи (28).
Теорема 4. Краевая задача Карлемана
![]() , (28)
, (28)
где
![]() , (29)
, (29)
разрешима в классе функций, ограниченных на бесконечности, и ее решение имеет вид
 (33)
(33)
где ![]() — решение интегрального уравнения
— решение интегрального уравнения ![]() , а
, а ![]() и определяется формулой
и определяется формулой
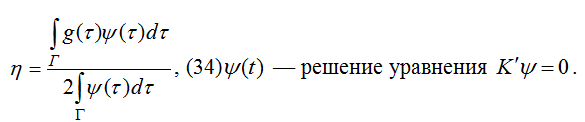
Доказательство. Согласно теореме 3 решение задачи (28) будем искать в виде (33), где плотность удовлетворяет условию (30). Предельные значения ![]() и
и ![]() имеют вид
имеют вид
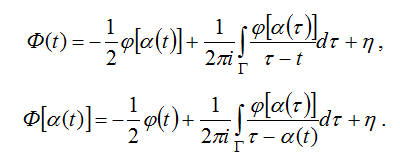
Отсюда с учетом условия (29) следует

то есть,
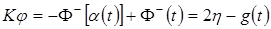 .
.
Условие разрешимости примет вид
![]() .
.
Отсюда для постоянной ![]() имеем (34).
имеем (34).
4. Однородная задача. Рассмотрим далее однородную краевую задачу
![]() . (35)
. (35)
В силу (2) из самого краевого условия следует, что для разрешимости задачи (35) необходимо выполнение условия (5). Поскольку ![]() обратный гомеоморфизм контура
обратный гомеоморфизм контура ![]() на себя, то, как легко заметить,
на себя, то, как легко заметить, ![]() , где
, где ![]() — число нулей функции
— число нулей функции ![]() в области
в области ![]() . Взяв индекс обеих частей равенства (35) и воспользовавшись этим фактом, а также свойствами индекса [7, с. 102], получим
. Взяв индекс обеих частей равенства (35) и воспользовавшись этим фактом, а также свойствами индекса [7, с. 102], получим
![]() .
.
Отсюда видно, что для разрешимости однородной краевой задачи Карлемана необходимо, чтобы индекс задачи ![]() был неотрицателен. Здесь необходимо различать два случая, когда коэффициент задачи
был неотрицателен. Здесь необходимо различать два случая, когда коэффициент задачи ![]() имеет нечетный или четный индекс. Функция сдвига
имеет нечетный или четный индекс. Функция сдвига ![]() имеет две неподвижные точки, то есть точки, где
имеет две неподвижные точки, то есть точки, где ![]() [12]. В силу (5) в этих точках
[12]. В силу (5) в этих точках ![]() , причем при чётном
, причем при чётном ![]() функция
функция ![]() принимает на них одинаковые значения, а при нечетном
принимает на них одинаковые значения, а при нечетном ![]() — различные [13, с. 158]. В случае нечетного
— различные [13, с. 158]. В случае нечетного ![]() , как видно из самого краевого условия (35), не существует решения задачи (35), нигде не обращающегося в нуль на контуре
, как видно из самого краевого условия (35), не существует решения задачи (35), нигде не обращающегося в нуль на контуре ![]() . Введем обозначение:
. Введем обозначение: ![]() , если
, если ![]() — четное число;
— четное число; ![]() , если
, если ![]() — нечетное.
— нечетное.
Пусть сперва, ![]() — четное число.
— четное число.
Рассмотрим вспомогательную краевую задачу
![]() , (36)
, (36)
где ![]() ,
, ![]() — значение
— значение ![]() в обеих неподвижных точках
в обеих неподвижных точках ![]() и
и ![]() . Легко убедиться, что
. Легко убедиться, что ![]() ,
, ![]() . Кроме того,
. Кроме того, ![]() . При этом
. При этом ![]() будет однозначной функцией. Логарифмируя краевое условие (36), получим
будет однозначной функцией. Логарифмируя краевое условие (36), получим
![]() , (37)
, (37)
причем ![]() .
.
Мы пришли к краевой задаче Карлемана по скачку. По теореме 2 задача (37) разрешима и имеет в классе аналитических функций, исчезающих на бесконечности единственное решение. Из (36) видим, что функция ![]() удовлетворяет краевому условию
удовлетворяет краевому условию
![]() . (38)
. (38)
Функцию ![]() назовем канонической функцией краевой задачи (35) с четным индексом. Каноническая функция аналитична всюду в области
назовем канонической функцией краевой задачи (35) с четным индексом. Каноническая функция аналитична всюду в области ![]() , и имеет в бесконечно удаленной точке нуль порядка
, и имеет в бесконечно удаленной точке нуль порядка ![]() . Во всех точках включая точек контура
. Во всех точках включая точек контура ![]() ,
, ![]() . Так как
. Так как ![]() всюду на
всюду на ![]() то в силу (38) будем иметь
то в силу (38) будем иметь
 . (39)
. (39)
Обозначив  проведем краевое условие (39) к виду
проведем краевое условие (39) к виду
![]() . (40)
. (40)
Искомая функция ![]() аналитична в области
аналитична в области ![]() всюду, кроме бесконечно удаленной точки, в которой она имеет полюс порядка
всюду, кроме бесконечно удаленной точки, в которой она имеет полюс порядка ![]() . Будем искать решение задачи (40) в виде
. Будем искать решение задачи (40) в виде
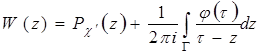 ,
,
где ![]() многочлен степени
многочлен степени ![]() ,
, ![]() удовлетворяет условию (9). Запишем по формулам Сохоцкого-Племеля предельные значения
удовлетворяет условию (9). Запишем по формулам Сохоцкого-Племеля предельные значения ![]() на
на ![]()
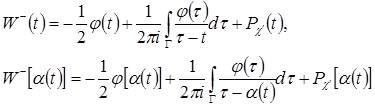
и поставив их в краевое условие (40), придем к интегральному уравнению

Условие разрешимости последнего уравнения имеет вид
![]() , (41)
, (41)
где: ![]() — решение союзного уравнения (18).
— решение союзного уравнения (18).
Пусть 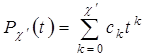 . Тогда путем замены
. Тогда путем замены ![]() и переобозначив
и переобозначив ![]() через
через ![]() , а также учитывая, что сдвиг меняет направление, получим
, а также учитывая, что сдвиг меняет направление, получим
![]() .
.
Теперь нетрудно убедиться, что условие (41) легко преобразовать к следующему виду
 . (42)
. (42)
Учитывая, что решения союзного уравнения (18) обладают свойством (21), приходим к выводу: при ![]() все интегралы левой части (42) равны нулю, и, следовательно, все постоянные
все интегралы левой части (42) равны нулю, и, следовательно, все постоянные ![]() произвольны. Если
произвольны. Если ![]() , то условие (42) в силу леммы 3 примет вид
, то условие (42) в силу леммы 3 примет вид
 .
.
Последнее равенство определяет коэффициент ![]() через остальные коэффициенты многочлена
через остальные коэффициенты многочлена ![]() , и, следовательно, общее решение задачи (40) при
, и, следовательно, общее решение задачи (40) при ![]() содержит на одну произвольную постоянную меньше, чем при
содержит на одну произвольную постоянную меньше, чем при ![]() . Тем самым доказана
. Тем самым доказана
Теорема 5. Однородная краевая задача Карлемана (35) с четным индексом ![]() в случае, если
в случае, если ![]() в неподвижных точках сдвига
в неподвижных точках сдвига ![]() , имеет
, имеет ![]() линейно независимых решений; эта задача имеет
линейно независимых решений; эта задача имеет ![]() линейно независимых решений, если в неподвижных точках
линейно независимых решений, если в неподвижных точках ![]() . Общее решение задачи дается формулой
. Общее решение задачи дается формулой

![]() ,
, ![]() ,
,
где: ![]() — многочлен степени не выше
— многочлен степени не выше ![]() с
с ![]() произвольными коэффициентами в случае
произвольными коэффициентами в случае ![]() и
и ![]() произвольными коэффициентами, если
произвольными коэффициентами, если ![]() ;
;
![]() — каноническая функция задачи с четным индексом;
— каноническая функция задачи с четным индексом;
![]() — решение интегрального уравнения Фредгольма
— решение интегрального уравнения Фредгольма
![]() .
.
Пусть теперь ![]() — нечетное число. В этом случае, как сказано выше, не существует решения краевой задачи (35), нигде не обращающегося в нуль на контуре
— нечетное число. В этом случае, как сказано выше, не существует решения краевой задачи (35), нигде не обращающегося в нуль на контуре ![]() . Обозначим через
. Обозначим через ![]() ту неподвижную точку, в которой
ту неподвижную точку, в которой ![]() . В таком случае любое решение
. В таком случае любое решение ![]() задачи (35) имеет вид
задачи (35) имеет вид ![]() , где
, где ![]() мероморфна в
мероморфна в ![]() и удовлетворяет граничному условию
и удовлетворяет граничному условию

Функция ![]() принадлежит классу
принадлежит классу 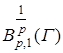 ,
, ![]() и отлична от нуля всюду на
и отлична от нуля всюду на ![]() . Кроме того, индекс функции
. Кроме того, индекс функции ![]() равен
равен ![]() и
и ![]()
![]() .
.
Таким образом, и в этом случае пришли к задаче с четным индексом. Проведем полное исследование.
Рассмотрим вспомогательную краевую задачу
![]() (43)
(43)
где ![]() . Нетрудно убедиться, что
. Нетрудно убедиться, что ![]() ,
, ![]()
![]() . Ясно, что
. Ясно, что ![]() однозначная функция. Прологарифмировав (43) имеем
однозначная функция. Прологарифмировав (43) имеем
![]() (44)
(44)
при этом ![]() .
.
По теореме 2 задача (44) безусловно разрешима и имеет в классе аналитических функций, исчезающих на бесконечности, единственное решение. Из (43) видно, что функция ![]() удовлетворяет краевому условию
удовлетворяет краевому условию
![]() (45)
(45)
Функцию ![]() назовем канонической функцией краевой задачи (35) с нечетным индексом. Каноническая функция
назовем канонической функцией краевой задачи (35) с нечетным индексом. Каноническая функция ![]() аналитична всюду в области
аналитична всюду в области ![]() и имеет в бесконечно удаленной точке нуль порядка
и имеет в бесконечно удаленной точке нуль порядка ![]() . Во всех остальных точках
. Во всех остальных точках ![]() , включая точек контура
, включая точек контура ![]() ,
, ![]() . Так как
. Так как ![]() на
на ![]() , то в силу (45) имеем
, то в силу (45) имеем
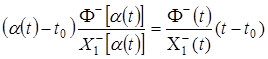 . (46)
. (46)
Обозначив

приведем (46) к виду
![]() . (47)
. (47)
Искомая функция ![]() аналитична всюду в области
аналитична всюду в области ![]() , кроме бесконечно удаленной точки, в которой она имеет полюс порядка
, кроме бесконечно удаленной точки, в которой она имеет полюс порядка ![]() . Решение задачи (47) будем искать в виде
. Решение задачи (47) будем искать в виде
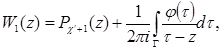
где ![]() многочлен степени
многочлен степени ![]() ,
, ![]() удовлетворяет условию (9). Используя формул Сохоцкого-Племеля, запишем предельные значения
удовлетворяет условию (9). Используя формул Сохоцкого-Племеля, запишем предельные значения ![]() на
на ![]()
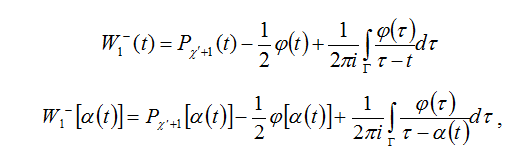
и подставив их в краевое условие (47), придем к следующему интегральному уравнению
![]() . (48)
. (48)
Условие разрешимости уравнения (48) имеет вид
![]() , (49)
, (49)
где: ![]() — решение союзного уравнения (18).
— решение союзного уравнения (18).
После некоторых преобразовании условие (49) приводится к виду
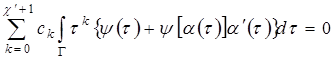 . (50)
. (50)
Учитывая, что решения союзного уравнения (18) обладают свойством (21) приходим к заключению: все интегралы в левой части (50) равны нулю, и, следовательно, все постоянные ![]() произвольны. Нами доказана следующая теорема.
произвольны. Нами доказана следующая теорема.
Теорема 6. Общее решение однородной задачи (35) с нечетным индексом ![]() аналитическое в
аналитическое в ![]() , представляется в виде
, представляется в виде
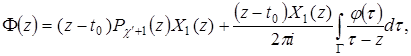
![]() ,
,
где: ![]() — та неподвижная точка
— та неподвижная точка ![]() , в которой
, в которой ![]() ,
,
![]() – многочлен степени не выше
– многочлен степени не выше ![]() с произвольными коэффициентами,
с произвольными коэффициентами,
![]() — решение интегрального уравнения
— решение интегрального уравнения
![]() ,
,
![]() — каноническая функция задачи (35) с нечетным индексом, определяемая формулой
— каноническая функция задачи (35) с нечетным индексом, определяемая формулой  , где
, где ![]() — решение интегрального уравнения
— решение интегрального уравнения ![]() ,
, 
6. Неоднородная задача. Перейдем к изучению неоднородной краевой задачи (1). Пусть ![]() .
.
В силу условия (5) к соответствующей однородной задаче применимы все рассуждения приведенные выше. В частности, каноническая функция X(z) удовлетворяет краевому условию (38). Выражая из условия (38) функцию G(t) и подставляя полученное выражение в краевое условие (1), имеем,
 . (51)
. (51)
Здесь ![]() , если
, если ![]() в обеих неподвижных точках
в обеих неподвижных точках ![]() ,
, ![]() — во всех остальных случаях.
— во всех остальных случаях.
Краевая задача (51) есть задача (7) с заданным скачком. Нетрудно показать, что условие (6) является условием разрешимости задачи (51). Решение краевой задачи (51) будем искать в виде
 (52)
(52)
где: ![]() — произвольный многочлен степени
— произвольный многочлен степени ![]() .
.
По формулам Сохоцкого-Племеля найдем предельные значения ![]() на контуре
на контуре ![]()
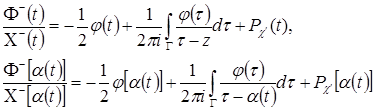
и подставив их в краевое условие (51) после некоторых преобразований придем к интегральному уравнению
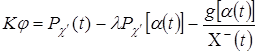 . (53)
. (53)
Интегральное уравнение (53) разрешимо при выполнении условия
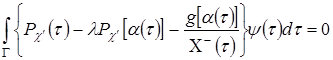 , (54)
, (54)
где: ![]() — нетривиальное решение союзного однородного уравнения
— нетривиальное решение союзного однородного уравнения ![]() . Используя условий (17) и (41) нетрудно показать, что при
. Используя условий (17) и (41) нетрудно показать, что при ![]() условие (54) выполняется для произвольных коэффициентов
условие (54) выполняется для произвольных коэффициентов ![]() , а в случае
, а в случае ![]() условие (54) определяет одну постоянную
условие (54) определяет одну постоянную ![]() через остальные.
через остальные.
Если индекс ![]() , то в формуле (52) следует положить
, то в формуле (52) следует положить ![]() . Чтобы
. Чтобы ![]() была аналитической в
была аналитической в ![]() функцией, необходимо требовать, кроме того, чтобы функция
функцией, необходимо требовать, кроме того, чтобы функция
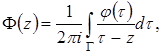
имела на бесконечности нуль порядка не ниже ![]() . Это означает необходимость выполнения
. Это означает необходимость выполнения ![]() условия разрешимости
условия разрешимости
![]() ,
, ![]() .
.
Кроме того, функция ![]() есть решение интегрального уравнения
есть решение интегрального уравнения
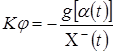 .
.
Следовательно, при ![]() должно выполняться еще одно условие разрешимости
должно выполняться еще одно условие разрешимости
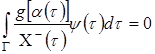 ,
,
где ![]() — нетривиальное решение союзного однородного уравнения
— нетривиальное решение союзного однородного уравнения ![]() . Полученные результаты резюмирует следующая
. Полученные результаты резюмирует следующая
Теорема 7. Неоднородная краевая задача (1) с индексом ![]() имеет
имеет ![]() — линейно независимых решений
— линейно независимых решений 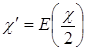 , если
, если ![]() , и
, и ![]() линейно независимых решений, если
линейно независимых решений, если ![]() . Общее решение задачи (1), аналитическое в
. Общее решение задачи (1), аналитическое в ![]() дается формулой
дается формулой

где ![]() — многочлен степени не выше
— многочлен степени не выше ![]() с
с ![]() произвольными коэффициентами в случае
произвольными коэффициентами в случае ![]() , и
, и ![]() — в случае
— в случае ![]() ,
, ![]() — каноническая функция,
— каноническая функция, ![]() есть решение интегрального уравнения
есть решение интегрального уравнения
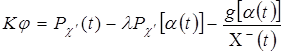 .
.
Если индекс ![]() , то краевая задача (1) имеет единственное решение, аналитическое в
, то краевая задача (1) имеет единственное решение, аналитическое в ![]() , определяемое формулой
, определяемое формулой
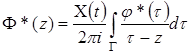 ,
, 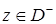 ,
,
где ![]() есть решение уравнения
есть решение уравнения ![]() . Для существование решения
. Для существование решения ![]() в случае
в случае ![]() необходимо и достаточно выполнение
необходимо и достаточно выполнение ![]() условий разрешимости
условий разрешимости
![]() ,
, ![]() . (55)
. (55)
при ![]() к условиям (55) добавляется еще одно условие
к условиям (55) добавляется еще одно условие

где ![]() — решение союзного однородного уравнения
— решение союзного однородного уравнения ![]() .
.
Список литературы:
- Айзенштат А.В. Задача Карлемана с разрывным сдвигом // Теория функций комплексного переменного и краевые задачи. Изд-во Чувашского ун-та. — 1974. — № 2. — С. 3—11.
- Альсейтов А.Г. Краевая задача Газемана в дробных пространствах Бесова // Материалы VIII международной научно-практической конференции «Естественные и математические науки в современном мире». Новосибирск. Изд. «СибАК». 1999. — С. 7—24.
- Альсейтов А.Г. О вполне непрерывности одного интегрального оператора в дробных пространствах О.В. Бесова // Тезисы II Международной научной конференции «Проблемы дифференциальных уравнений, анализа и алгебры», Актобе, 1999. — С. 7.
- Альсейтов А.Г. Об одном интегральном операторе в дробных пространствах О.В. Бесова // Поиск. Серия естест. наук. — 1999. — № 5. — С. 199—205.
- Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения. М.: Наука, 1975. — 480 с.
- Блиев Н.К. Обобщенные аналитические функции в дробных пространствах. Алма-Ата: Наука, 1985. — 160 с.
- Гахов Ф.Д. Краевые задачи. М.: Наука, 1977. — 640 с.
- Голузин Г.М. Геометрическая теория функций комплексного переменного. М.: Наука, 1966. — 540 с.
- Квеселава Д.А. Решение одной граничной задачи теории функций // Докл. АН СССР. — 1946. — Т. 53. — № 8. — С. 683—686.
- Квеселава Д.А. Об одной граничной задачи теории функций // Сообщ. АН. Груз. ССР. — 1946. — Т. 7. — № 9—10. — С. 609—614.
- Квеселава Д.А. Решение одной граничной задачи теории функций Т. Карлемана // Докл. АН СССР. — 1947. — Т. 55. — № 8. — С. 683—686.
- Квеселава Д.А. Некоторые граничные задачи теории функций // Труды Матем. ин-та. Груз. ССР. — 1948. — Т. 16. — С. 39—80.
- Литвинчук Г.С. Краевые задачи и сингулярные интегральные уравнения со сдвигом. М.: Наука, 1977. — 448 с.
- Литвинчук Г.С. О некоторых краевых задачах Римана со смещениями // Изв. вузов, матем. — 1961. — № 6. — С. 71—81.
- Манджавидзе Г.Ф., Хведелидзе Б.В. О задаче Римана-Привалова с непрерывными коэффициентами // Докл. АН СССР. — 1958. — Т. 123. — № 5. — С. 791—794.
- Мельник И.М. О краевой задаче Карлемана с разрывными коэффициентами // Сообщ. III конф. Ростовск. матем. об-ва. Ростов-н/Д. — 1969. — Вып. 2. — С. 41—49.
- Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Физматгиз, 1968. — 512 с.
- Симоненко И.Б. Краевая задача Римана для n пар функций с измеримыми коэффицентами и ее применение к исследованию сингулярных интегралов в пространствах Lp с весами // Изв. АН СССР. Сер. матем. — 1964. — Т. 28. — № 2. — С. 277—306.
- Симоненко И.Б. Краевые задачи Римана и Римана-Газемана с непрерывными коэффициентами // Исследования по современным проблемам теории функций компл. перем. М.: Физматгиз. 1961. — С. 380—389.
- Чакветадзе С.С. Обобщенная граничная задача Гильберта для нескольких неизвестных функций с разрывными коэффициентами // Тр. Горийского пед. ин-та. — 1961. — № 7. — С. 155—164.
- Чернецкий В.А. О конформной эквивалентности краевой задачи Карлемана краевой задачи Римана на разомкнутом контуре // Докл. АН СССР. — 1970. — Т. 190. — № 1. — С. 54—56.
- Чернецкий В.А. Краевая задача Карлемана для многосвязной области. Новосибирск (Деп. в ВИНИТИ, — 1971, — № 3782-71. — 32 с.).
- Чибрикова Л.И. О применении римановых поверхностей при исследовании плоских краевых задач и сингулярных интегральных уравнений // Труды семинара по краевым задачам Казанского университета. — 1970. — вып. 7. — С. 28—44.
- Чибрикова Л.И. Особые случаи обобщенной задачи Римана // Уч. зап. Казанского ун-та. — 1952. — Т. 112. — № 10. — С. 129—154.
- Schaeffer A.C. and Spencer D.C. Coefficients regions of schlicht functions, Amer. Soc. Colloquim, Publ. 35, (1950).
- Yong Er-gian. On the sewing theorem, Chinese Math.5, 1 (1964).
дипломов


Оставить комментарий