РАЗЛИЧНЫЕ  СТАТИСТИКИ  В  ОТРИЦАТЕЛЬНОЙ  ПОЛИНОМИАЛЬНОЙ  СХЕМЕ

Нуртаева  Дана  Калдыбаевна

магистр,  старший  преподаватель  Университета  «Туран»,  Казахстан,  г.  Алматы

E-mail: 

 

DIFFERENT  STATISTICS  IN  THE  NEGATIVE  POLYNOMIAL  SCHEME

Nurtayeva  Dana  Kaldybayevna

master,  senior  teacher  of  University  “Turan”,  Kazakhstan,  Almaty

 

АННОТАЦИЯ

В  статье  рассматриваются  критерии  значимости  для  проверки  непараметрических  гипотез,  основанные  на  статистиках,  полученных  в  результате  изучения  предельного  поведения  отрицательного  полиномиального  распределения.

ABSTRACT

Significance  tests  for  checking  up  of  the  nonparametric  hypothesis  based  on  the  statistics,  which  have  been  received  in  the  result  of  the  analysis  of  the  utmost  action  of  the  negative  polynomial  distribution,  are  examined  in  the  given  article.

 

Ключевые  слова:  отрицательное  полиномиальное  распределение;  непараметрические  гипотезы.

Keywords:  negative  polynomial  distribution;  nonparametric  hypothesis.

 

Пусть    простая  выборка  объема    из  генеральной  совокупности  с  распределением  .  Будем  считать,  что  относительно    верна  одна  из  двух  гипотез:  либо  гипотеза  ,  состоящая  в  том,  что  ,  либо  дополнительная  гипотеза  ,  которая  означает  что  .

Для  проверки    против    отрезок  ,  на  котором  сосредоточены    и  ,  разобьем  на  непересекающиеся  интервалы    и  пусть    число  элементов  выборки  в  .  Положим  далее,  что    соответственно  плотности  распределения    и  ,    и    интегрируемы  по  Риману.  Для  простоты  будем  считать,  что  длина  отрезка    конечна,  a  .

Сделанные  допущения  позволяют  записать

 

.

 

Введем  обозначения

 

,

,        (1)

.

 

Если  объем  выборки    фиксирован,  то  рассмотренная  методика  проверки  гипотез  приводит  к  хорошо  известному  критерию  хи-квадрат  [6,  с.  453],  [5,  с.  255],  связанному  с  полиномиальным  (мультиномиальным)  распределением. 

Изучение  этого  распределения  и  полученные  нормировки  приводят  к  линейным  статистикам,  использование  которых  позволили  строить  дополнительные  критерии  для  проверки  непараметрических  гипотез,  отличных  от  критерия  хи-квадрат.  Более  того,  полученные  перенормировки  позволяют  сделать  некоторые  усовершенствования  и  для  самого  критерия  хи-квадрат.  Изложение  этих  вопросов  приведены  в  [1,  с.  21],  [2,  с.  42].

При  проверке  непараметрических  гипотез,  используется  модель,  приводящая  к  отрицательному  полиномиальному  распределению.

Используя  приведенные  данные  в  начале  статьи,  рассматривается  выборка  до  появления    -  го  появления  выборочного  значения  в  интервале    при  этом  будем  полагать,  что  в  интервалах    имеются  выборочных  значений  соответственно.  Отметим,  что  компоненты    являются  возможными  значениями  случайного  вектора  ,  где  .

В  этой  связи,  мы  сделаем  следующее  соглашение,  которое  поможет  нам  избежать  громоздких  обозначений.  В  дальнейшем,  по  мере  необходимости,  компоненты  вектора    будем  использовать  и  как  возможные  значения  и  как  случайные  величины.  Если  такое  соглашение  может  привести  к  недоразумениям,  то  мы  будем  использовать  более  подробные  рассуждения.

Приведем  необходимые  результаты  для  отрицательного  полиномиального  распределения,  изложенные  в  [7,  с.  63],  которые  послужат  нам  основой  для  построения  статистик,  используемых  для  проверки  непараметрических  гипотез.

Исходя  из  приведенных  данных,  отрицательное  полиномиальное  распределение  имеет  вид

 

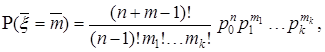                       (2)

 

где  ,  ,  .

Следующий  результат,  изложенный  в  [7,  с.  63],  относится  к  аппроксимации  вероятностей  (2)  и  является  аналогом  хорошо  известной  локальной  теоремы  для  полиномиального  распределения  [4,  с.  88].

Теорема  1.  При  ,  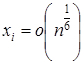  и  ,

 

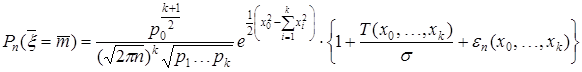(3)

 

где

 

,

.

 

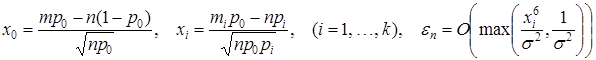В  формуле  (3)  привлекает  к  себе  внимание  квадратичная  форма 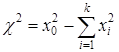 ,  точнее  ее  знакоопределенность.  Дело  в  том,  что  если    в  некоторой  области  принимает  положительные  значения,  то  правая  часть  в  (3)  может  оказаться  больше  единицы.  Оказалось,  что  указанная  квадратичная  форма  является  отрицательно  определенной.  Это  положение,  с  помощью  ортогонального  преобразования  типа  Хельмерта,  получено  в  [7,  с.  63].  Более  того,  с  помощью  этого  преобразования,  результат  теоремы  1  приводится  к  преобразованной  форме,  который  позволяет  перейти  к  интегральным  теоремам.

Теорема  2.  Пр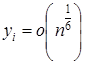и  ,    и    имеет  место

 

,

 

где

 

,

 

.

 

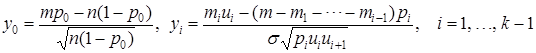
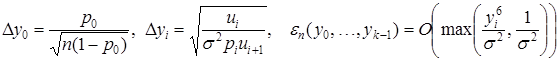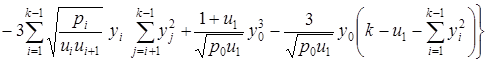Полагая    случайными,  определим  моменты  величин  .

Теорема  3.  Имеют  место  следующие  соотношения,

.

Доказательство.  Напомним,  что  .

Известно,  что  моменты  для  отрицательного  полиномиального  распределения  имеют  вид,

 

 

Нетрудно  подсчитать,  что

 

 

Используя  приведенные  соотношения,  будем  иметь:

 

.

 

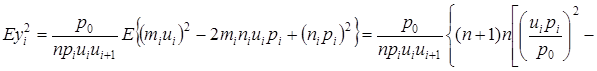
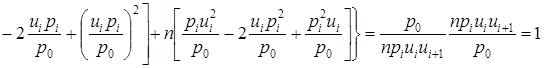При    и  ,  имеем

 

.

 

Теорема  доказана.

На  основании  результатов  в  теоремах  2  и  3,  рассмотрим  следующие  статистики: 

 

 

 

 

где  соответствующие  величины  определены  в  (1).

На  основании  результатов  в  [7,  с.  63],  запишем  предельные  распределения  введенных  статистик.  При    имеем

 

                               (4)

 

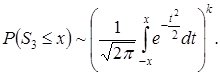
Приведенные  статистики  могут  быть  использованы  для  построения  соответствующих  критериев  значимости,  при  проверке  непараметрических  гипотез.  В  дальнейшем,  нас  будет  интересовать  вопрос  о  поведении  мощностей  этих  критериев.  Первой  задачей  является  изучение  мощности  критерия,  связанного  с  линейной  статистикой  .  При  этом,  задача  состоит  в  том,  чтобы  на  основании  выборочных  значений  подобрать  коэффициенты    так,  чтобы  они  доставляли  максимум  мощности  рассматриваемого  критерия.

Теорема  4.  Наибольшая  мощность  критерия,  основанного  на  линейной  статистике  ,  достигается  при  значениях

 

      .

 

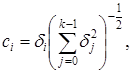
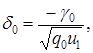
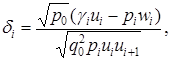
Доказательство.  Из  теоремы  3  следует,  что

 

 

Следовательно,  при  выполнении  нулевой  гипотезы  статистика    имеет  стандартный  нормальный  закон  распределения.  Рассматривая  двухсторонний  критерий  и  задавая  уровень  значимости  ,  определим    из

 

.

 

Выражение  для  функции  мощности  примет  вид:

 

.                                                                         (5)

 

Таким  образом,  наша  задача  свелась  к  нахождению  условного  распределения  .

Покажем,  что  при  выполнении  гипотезы    статистика    в  пределе,  при    имеет  нормальный  закон  распределения.  Для  этого  нам  потребуются  преобразования,  приспособленные  для  гипотез    и    соответственно.

При  выполнении  гипотезы  ,  приведем  прямое  и  обратное  преобразования:

 

,

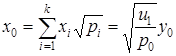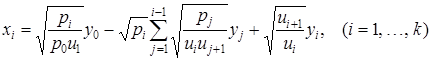,  (6)

.

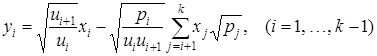При  выполнении  гипотезы    прямое  и  обратное  преобразования  имеют  вид:

 

,

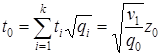,     (7)

.

 

Нетрудно  заметить,  что  соотношения  в  (6)  и  (7)  имеют  одну  и  ту  же  структуру,  различие  проявляется  в  обозначениях:  при  гипотезе    мы  используем  вероятности  ,  а  при  альтернативной  гипотезе    вероятности  .  Отсюда,  соответственно    заменяется  на  .

Из  соотношений  (1)  следует,

 

,            (8)

.

 

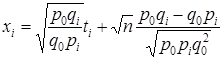На  последующем  этапе  доказательства,  нам  потребуется  выразить    через  .  Для  этого,  выражение  для    из  (8)  подставим  в  соотношение  для    в  (6).  В  результате  получим  следующее  промежуточное  выражение,

 

.

 

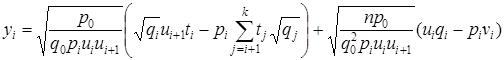Определяя  из  (7)  выражение  для 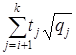   и  подставляя  его  в  предыдущее  соотношение  получим,

 

.

 

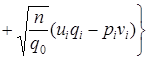Подставляя  выражение  для    из  (7)  в  последнее  выражение  и  проведя  соответствующие  выкладки,  получим

 

.       (9)

 

Напомним,  что  при  выполнении  гипотезы    имеем,

 

.         (10)

 

В  силу  того,  что  выражение  для    не  определяется  закономерностью  для  всех  остальных  ,  ,  то  вычисляемые  моменты,  с  участием    выделим  отдельно.

Так  как 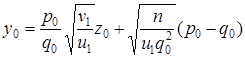 ,  то  .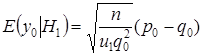

Далее,  на  основании  (10),  из  (9)  получим,  .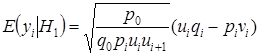

Приступим  к  нахождению  дисперсий,  при  выполнении  гипотезы  .

 

,

.

 

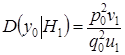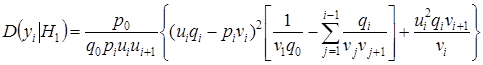Упростим  выражение  для  суммы,

 

.

 

Следовательно,  .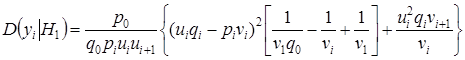

Вычислим  ковариации,  при  выполнении  .

 

,  .

 

Следующие  ковариации  определяются  при 

 

.

 

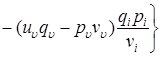Для  нахождения  предельных  соотношений  вычисленных  моментов,  при    отметим,  что  .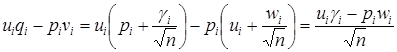

Таким  образом,  на  основании  последнего  соотношения,  вычисленные  ранее  моменты,  примут  вид:

 

,  ,  ;

;

;

,  ;

.

 

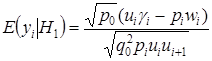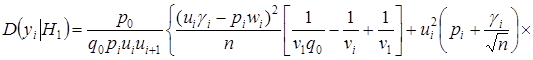
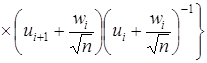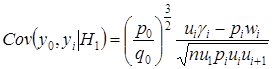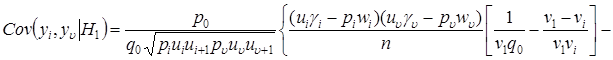
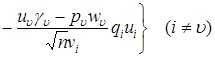Переходя  к  пределу  при    в  полученных  выражениях  для  моментов  получим,

 

,

,  ,

,  ,

.

 

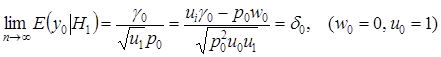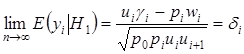Определим  предельный  закон  распределения  при    для  величин  ,  при  выполнении  гипотезы  .  Напомним,  что  при  выполнении  гипотезы  ,  величины    имеют  стандартный  нормальный  закон  распределения.  С  другой  стороны,  из    следует,  что  при  ,  .  Отсюда  делаем  вывод,  что  при    величины  ,  при  выполнении  гипотезы  ,  имеют  нормальный  закон  распределения  c  моментами,  определенными  в  (10)  и  к  тому  же,  являющимися  независимыми.  Из  сказанного  следует,  что  статистика    имеет  нормальный  закон  распределения  с  параметрами 

 

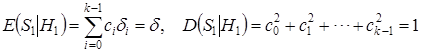.             (11)

 

Следовательно,  на  основании  (5),  при 

 

.                         (12)

 

Правая  часть  выражения  (12)  ведет  себя  монотонно  и  будет  тем  больше,  чем  больше  значение  .  Следовательно,  мы  приходим  к  классической  задаче  на  условный  экстремум,  т.е.  в  соотношениях  (11)  нужно  подобрать  такие  ,  которые  доставляют  максимум  для  значения  .

Запишем  решение  этой  задачи,  .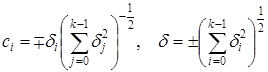

Теорема  4  доказана.

Замечание  1  Поясним  вероятностный  смысл  параметра  .  Для  этого  нам  потребуется  лемма,  рассмотренная  в  [1,  с.21],  [2,  с.42].

Лемма.  Пусть  квадратичная  форма  определяется  соотношениями

 

 

тогда,  с  помощью  ортогонального  преобразования

 

,

 

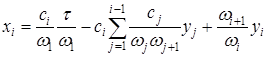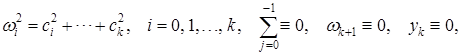
приводится  к  виду  .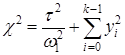

Рассмотрим  квадратичную  форму 

 

.

 

Применяя  лемму  и  учитывая,  что    получим,

 

.

 

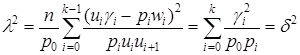Таким  образом,  ,  являясь  параметром  сдвига  в  (12),  характеризует  расхождение  между  гипотезами.  Сам  факт  того,  что  мощность  критерия  увеличивается  с  увеличением  расхождения  между  гипотезами    и  ,  не  является  примечательным,  важно,  что  из  всех  линейных  критериев,  он  является  оптимальным.

Замечание  2  Рассмотрим  обоснование  выбора  плотности  для  альтернативной  гипотезы  ,  т.  е.  вид  .  Для  этого,  как  и  в  [2,  с.  42],  рассмотрим  расширенную  альтернативную  гипотезу  ,  связанную  с  плотностью  .

Из  этого  следует,  что  при  ,  .  Так  как  при  выполнении  гипотезы  ,  величины    имеют  нормальный  закон  распределения,  то  при    и  выполнении  гипотезы  ,  величины    также  имеют  нормальный  закон  распределения.  Представим  соответствующие  моменты  для  ,  при  выполнении  гипотезы  .  При    имеем,

 

,

.

 

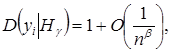
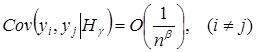Следовательно: 

1)  При    и  ,  математическое  ожидание  стремится  к  нулю,  также  как  и  ковариация,  а  дисперсия  стремится  к  единице.  При  этом  мощность  критерия  совпадает  с  размером  критерия  ,  при  любых  альтернативах  .  Другими  словами,  критерий  не  различает  гипотезы    и  .

2)  Пусть  .  В  этом  случае,  при  ,  математическое  ожидание  стремится  к  бесконечности,  не  зависимо  от  .  То  есть,  хотя  мощность  критерия  и  стремится  к  1,  но  критерий  также  не  отличает  альтернативы  по  .

3)  Содержательным  случаем  является  .

Как  следует  из  (4)  статистика    имеет  распределение  хи-квадрат  с  -степенями  свободы.  Следовательно,  критерий,  основанный  на  статистике  ,  является  аналогом  классического  критерия  ,  мощность  которого  определяется  с  помощью  нецентрального  хи-квадрат  распределения.  Наш  случай  вывода  функции  мощности  критерия,  основанного  на  статистике  ,  практически  ничем  не  отличается  от  вывода  функции  мощности  для  критерия  ,  рассмотренного  в  [2,  с.  42].

Задавая  уровень  значимости  ,  определим  критическую  точку  .  Функция  мощности  рассматриваемого  критерия  определяется  равенством,

 

.

 

Теорема  5.

 

 

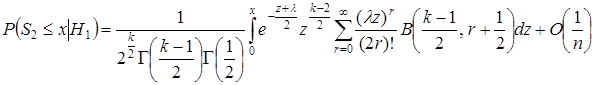
где 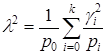 ,    —  бета  функция.

Задавая  уровень  значимости  ,  на  основании  (7)  определим  критическое  значение  .  В  этом  случае,  функция  мощности  имеет  вид

 

.

 

По  аналогии  с  [1,  с.  21],  для  функции  мощности  имеем  следующее  утверждение.

Теорема  6.

 

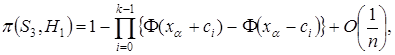  где  ,  .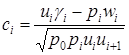

 

Возвращаясь  к  величинам    в  (9)  и  полагая  их  случайными  нам  известно,  что    независимые  (точнее,  асимптотически  независимые),  одинаково  распределенные  величины,  где  каждое  из  них  имеет  стандартный  нормальный  закон  распределения.  Такое  положение  вещей  позволяет  рассмотреть  еще  некоторые  критерии,  основанные  на  распределениях  Стьюдента  с  ()  степенями  свободы,  Фишера  с  ()  степенями  свободы  соответственно.  Сведения  об  этих  распределениях  можно  получить  в  [3,  с.  115].

 

Список  литературы:

1.Аренбаев  Н.К.,  К  проверке  статистических  гипотез,  Вестник  КазГУ,  (математика,  механика,  информатика),  4,  Алматы,  1996.  —  С.  21—28.

2.Аренбаев  Н.К.,  О  двух  критериях  значимости,  Вестник  КазНУ,  (серия  математика,  механика,  информатика),  2(41),  Алматы,  2004.  —  С.  42—50.

3.Большев  Л.Н.,  Смирнов  Н.В.,  Таблицы  математической  статистики,  М.:  «Наука»,  1983.  —  416  с.

4.Калинин  В.М.,  Предельные  свойства  вероятностных  распределений,  Труды  ордена  Ленина  Математического  института  им.  Стеклова  В.А.,  (Исследования  по  математической  статистике),  104,  Л.:  «Наука»,  1968.  —  С.  88—134.

5.Кендалл  М.Дж.,  Стьюарт  А.,  Теория  распределений,  М.:  «Наука»,  1966.  —  566  с.

6.Крамер  Г.,  Математические  методы  статистики,  М.:  Мир,  1975.  —  648  с.

7.Нуртаева  Д.К.,  Предельное  поведение  отрицательного  полиномиального  распределения  при  нормировке  содержащей  произвольный  параметр,  Вестник  КазНУ,  (серия  математика,  механика,  информатика),  №  1(52),  Алматы,  2007.  —  С.  63—70.