АСИМПТОТИКА  РЕШЕНИЯ  СИНГУЛЯРНО  ВОЗМУЩЕННОГО  ЭЛЛИПТИЧЕСКОГО  УРАВНЕНИЯС  КРАТНОЙ  ТОЧКОЙ  ПОВОРОТА  ВНУТРИ  ОБЛАСТИ

Турсунов  Дилмурат  Абдиллажанович

канд.  физ.-мат.  наук,  доцент  ОшГУ,  г.  Ош

E-mail:  dosh2012@mail.ru

ASYMPTOTICS  OF  SOLUTIONS  OF  SINGULARLY  PERTURBED  ELLIPTIC  EQUATIONS  WITH  THE  MULTIPLE  TURNING  POINT  IN  AREA

Dilmurat  Tursunov

сandidate  of  physics  and  mathematics  sciences,  associate  professor  of  Osh  State  University,  Osh

АННОТАЦИЯ

Целью  данной  работы  является  построить  равномерную  асимптотику  решения  задачи  Дирихле  для  бисингулярно  возмущенного  эллиптического  уравнения  в  круге.  Соответствующее  невозмущенное  уравнение  имеет  кратную  точку  поворота  внутри  круга.  Применяется  новый  метод  —  обобщенный  метод  погранфункций,  который  является  аналогом  метода  погранфункций.  Получена  равномерная  асимптотика  решения  поставленной  задачи.

ABSTRACT

The  aim  of  this  paper  is  to  construct  a  uniform  asymptotic  solution  of  the  Dirichlet  problem  for  the  bisingularly  perturbed  elliptic  equation  in  a  circle.  The  corresponding  unperturbed  equation  has  a  multiple  turning  point  within  the  circle.  A  generalized  method  of  boundary  functions  has  been  applied.  The  proposed  method  is  analog  of  the  boundary  functions.  The  uniform  asymptotic  solution  of  the  problem  was  constructed.

Ключевые  слова:  асимптотика;  точка  поворота;  задача  Дирихле;  погранфункций;  эллиптические  уравнения;  асимптотический  ряд;  уравнение  Гельмгольца.

Keywords:  asymptotic;  turning  point;  the  Dirichlet  problem;  boundary  functions;  elliptic  equations;  asymptotic  series;  Helmholtz  equation.

Работа  выполнена  при  поддержке  гранта  РФФИ  по  проекту  №  13-01-90903  мол_ин_нр

Постановка  задачи.  Рассмотрим  задачу  Дирихле  для  эллиптического  уравнения

eD_rfu–rⁿ  u=f(r,f),  (r,f)ÎD={(r,f)|0£f<2p,  0£r<1},  (1)

u(1,f,e)=0,  (2)

где 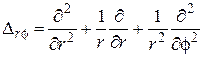 ,  u=u(r,f,e),  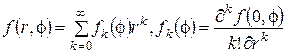,  0<e<<1  —  малый  параметр.

Аналогичные  задачи  к  задаче  (1)—(2),  методом  сращивания,  рассмотрены  в  работах  [1],  [4],  [5]  и  в  цитируемых  в  этих  работах.  А  в  работе  [3]  рассмотрен  случай  n=1.

Как  и  раньше,  чтобы  убедится,  что  решение  соответствующего  невозмущенного  уравнения  имеет  особенность,  рассмотрим  структуру  внешнего  разложения  решения  задачи  (1),  которое  ищем  в  виде:

,                             (3)

где:  V  —  это  пока  формальный  ряд.  Подставляя  (3)  в  (1)  и  приравнивая  коэффициенты  при  одинаковых  степенях  e,  получим  рекуррентную  систему  уравнений:  –rⁿv₀(r,f)=f(r,f),  rⁿv_k(r,f)=D_rfv_k–1(r,f),  kÎN.

Отсюда  определяются  все  :

v₀(r,f)  =  –f(r,f)/rⁿ,         v_k(r,f)=D_rfv_k–1(r,f)/rⁿ,  kÎN.

Заметим,  что  при  r=0  все  эти  функции  v_k(r,f)  имеют  нарастающие  особенности:

v_k(r,f)=О(1/r^n+k(n+2)),  k=0,1,2,...  .

Поэтому  задача  (1)-(2)  является  бисингулярной.  В  окрестности  r=0,  имеем:

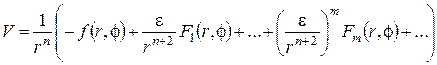,  при  e®0,

где  ,  k=1,2,...  .

В  окрестности  r=0  ряд  (3)  не  только  не  приближает  решение  u(r,f,e),  но  даже  теряет  асимптотический  характер.

Построение  ФАР  решения.  Решение  задачи  (1)-(2)  будем  искать  в  виде:

u(r,f,e)=+v₀(r,f)+p₀(h,f²)+R(r,f),  (4)

где  h=(1–r)/e^1/2,  e=mⁿ⁺²,  t=r/m.

Учитывая  граничное  условие  (2)  имеем:

u(1,f,e)=+v₀(1,f)+p₀(0,f²)+R(1,f)=0,

w_k(1/m,f)=0,  k=  –n,–n+1,...,–1;                                    (5)

p₀(0,f²)=–v₀(1,f),                                          (6)

R(1,f)=0.                                           (7)

Подставляя  (4)  в  (1)  получим:

eD_rfv₀–rⁿv₀++eD_hfp₀–(1–e^1/2h)ⁿp₀+

+eD_rfR–rⁿR  =f(r,f)–H(r,f)+H(mt,f),  (8)

где 

,.

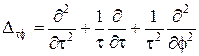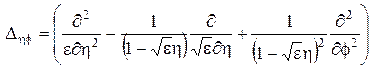Здесь  мы  в  правую  часть  уравнения  прибавили  и  убавили  одну  и  ту  же  функцию  Н(r,f),  которую  определим  ниже.

Из  равенства  (8)  получим:

eD_rfv₀–rⁿv₀+  +(–p₀)+О(e^1/2)+

+eD_rfR–rⁿR=f(r,f)–H(r,f)+H(tm,f).

Отсюда,  учитывая  (5)—(7)  получим:

–rⁿv₀=f(r,f)–H(r,f);  (9)

=  H(tm,f),  w_k(1/m,f)=0,  k=  –n,–n+1,...,–1;     (10)

–p₀=0,  p₀(0,f²)=–v₀(1,f);             (11)

eD_rfR–rⁿR  =О(e^1/2)–  eD_rfv₀,  R(1,f)=0.                (12)

Из  равенства  (9)  определяем  v₀(r,  f):  v₀(r,f)=  –(f(r,f)–H₀(r,f))/rⁿ.

Определим  неизвестную  функцию  Н(r,f)  так  чтобы  v₀(r,f)ÎC^¥().  Значит,  H(r,f)=.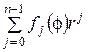

Следовательно,

v₀(r,f)= 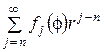 –.                       (13) 

Задачу  (10)  запишем  в  следующем  в  виде:

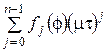=  ,  w_k(1/m,f)=0.

Приравнивая  по  степеням  m,  получим:

,  w_k(1/m,f)=0,  k=  –n,–n+1,...,–1.  (14)

Уравнение    приводим  к  неоднородному  уравнению  Гельмгольца.  Пусть  ,  .  Вычисляя  соответствующие  производные  и  подставляя  их  в  уравнение 

,

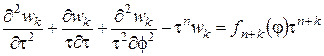получим:  .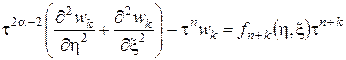

Отсюда,  при  a=(n+2)/2  имеем:  .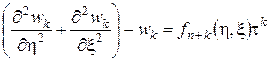

Так  как  ,  ,  то  ,  отсюда  следует,  что  .

Следовательно, 

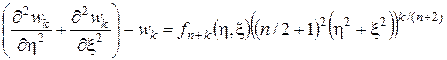.               (15)

При  –¥<h<¥,  –¥<x<¥,  уравнение  (15)  имеет  единственное  решение  [2]:

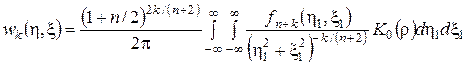,          (16)

где:  ,  K₀(r)  —  функция  Макдональда  (моди-фицированная  функция  Бесселя). 

Асимптотику  решения  задачи  (14)  при  t®¥,  ищем  в  виде

  (17)

Подставляя  (17)  в  (14)  имеем:

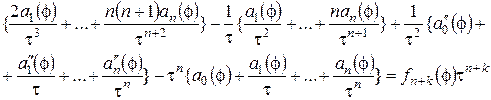
Отсюда 

при  k=  –n:  a_j(f)º0,  j=0,1,..,n–1,  a_n(f)=  –f₀(f),...;

при  k=  –n+1:  a_j(f)º0,  j=0,1,..,n–2,  a_n–1(f)=  –f₁(f),...;

...

при  k=  –1:  a₀(f)º0,  a₁(f)=  –f_n–1(f),...  .

Следовательно,  справедливы  равенства:

,

,

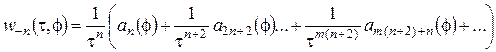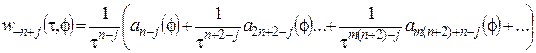т.  е.  ,  при  t®¥,  j=0,1,2,...,n–1.

Для  "k,  w_k(t,  f)®0  при  t®¥;  w_k(t,  f)ÎС^¥(),  k=–n,–n+1,…,–1.

Задача  (11)  имеет  единственное  решение  представимое  в  виде:

,                          (18)

.

Оценка  остаточного  члена  R(r,f).  Задачу  (12)  запишем  в  виде 

eD_rfR–rⁿR  =  О(e^1/2),  R(1,f)=0.

Пусть  R(r,f)=O(e^1/2)Z(r,f)/mⁿ,  m=e^1/(n+2),  r=mt,  тогда 

D_tfZ–tⁿZ=1,  Z(1/m,f)=0.

Учитывая  решение  задачи  (14)  имеем:

Z(r,f)=О(1),  Z(1/m,f)=O(1/tⁿ),  при  m®0,  t®¥.

Отсюда  следует,  что  |R(r,f)|=O(e^n/(2n+4)).

Нами  доказана

Теорема.  Если  f(r,f)ÎC^¥(),  f  (0,0)≠0,  тогда  для  решения  задачи  (1)-(2)  справедливо  асимптотическое  разложение 

,  при  e®0,

где:  v₀,  w_k,,  p₀  —  функции,  определяемые  из  равенств  (13),  (16),  (18).

Список  литературы:

1.Ильин  А.М.  Согласование  асимптотических  разложений  краевых  задач.  М.:  Наука,  1989.  —  334  с.

2.Полянин  А.Д.  Справочник  по  линейным  уравнениям  математической  физики.  М.:  ФИЗМАТЛИТ,  2001.  —  576  с.

3.Турсунов  Д.А.  Аналог  метода  погранфункции  для  бисингулярно  возмущенного  эллиптического  уравнения  //  Сб.  научн.трудов  X  межд.науч.конф.  Молод.  учен.  «Перспективы  развития  фунд-х  наук»  Россия,  Томск,  2013.  —  С.  623—626.

4.Eckhaus  W.,  Boundary  Layers  in  Linear  Elliptic  Singular  Perturbation  Problems,  SIAM  Review,  —  Vol.  14,  —  №  2  (Apr.,  1972),  —  pp.  225—270.

5.Shagi-di  Shih  and  r.  Bruce  Кellogg,  Asymptotic  analysis  of  a  singular  perturbation  problem,  SIAM  J.  Math.  Anal.  —  Vol.  18,  —  №  5,  (Sept  1987),  —  pp.  1467—1511.