АСИМПТОТИКА  РЕШЕНИЯ  СИНГУЛЯРНО  ВОЗМУЩЕННОГО  ОБЫКНОВЕННОГО  ДИФФЕРЕНЦИАЛЬНОГО  УРАВНЕНИЯ  С  ДВУМЯ  ТОЧКАМИ  ПОВОРОТА  В  КОМПЛЕКСНОЙ  ПЛОСКОСТИ

Турсунов  Дилмурат  Абдиллажанович

канд.  физ.-мат.  наук,  доцент  ОшГУ,  г.  Ош

E-mail:  dosh2012@mail.ru

ASYMPTOTICS  OF  SOLUTIONS  OF  SINGULARLY  PERTURBED  ORDINARY  DIFFERENTIAL  EQUATIONS  WITH  TWO  TURNING  POINTS  IN  THE  COMPLEX  PLANE

Dilmurat  Tursunov

candidate  of  physics  and  mathematics  sciences,  associate  professor  of  Osh  State  University,  Osh

АННОТАЦИЯ

Целью  данной  работы  является  построить  равномерную  асимптотику  решения  обыкновенных  дифференциальных  уравнений  с  простой  точкой  поворота  в  комплексной  плоскости,  когда  нарушается  условие  асимптотической  устойчивости.  Для  оценки  интегралов  применяется  метод  стационарной  фазы  и  метод  перевалов.  Построена  равномерная  асимптотика  решения  поставленной  задачи.  Асимптотика  решения  рассматриваемой  задачи  существенно  зависит  от  неоднородной  части  рассматриваемого  уравнения.

ABSTRACT

The  aim  of  this  paper  is  to  construct  a  uniform  asymptotic  solution  of  ordinary  differential  equations  with  a  simple  turning  point  in  the  complex  plane  when  a  condition  of  asymptotic  stability  is  violated.  The  method  of  stationary  phase  and  the  passes  method  are  used  to  evaluate  the  integrals.  The  uniform  asymptotic  solution  of  the  problem  was  constructed.  Asymptotic  of  the  solution  of  the  problem  essentially  depends  on  the  inhomogeneous  part  of  the  equation.

Ключевые  слова:  асимптотика;  точка  поворота;  условия  устойчивости;  стационарная  фаза;  точка  перевала;  малый  параметр.

Keywords:  asymptotic;  turning  point;  stability  conditions;  stationary  phase;  passes  point;  small  parameter.

Работа  выполнена  при  поддержке  гранта  РФФИ  по  проекту  №  13-01-90903  мол_ин_нр

Теорию  запаздывания  потери  устойчивости  в  системах  общего  вида  построены  в  работах  А.И.  Нейштадта  [2].  Далее  появились  работы  [1],  [3]  и  др.  Численными  и  аналитическими  методами  явление  запаздывание  потери  устойчивости  изучалось  в  системах,  встречающихся  в  физике  лазеров,  химической  кинетике,  биофизике,  в  модифицированной  системе  Циглера  и  в  моделировании  безопасных  процессов  горения  с  максимальной  температуры.  Во  всех  этих  перечисленных  работах  невозмущенное  (предельное)  уравнение  имеет  тривиальное,  т.е.  гладкое  решение  в  рассматриваемой  области.  В  нашем  случае  решение  предельного  уравнения  имеет  особенность.

Рассмотрим  задачу

ex¢(t,e)=A(t)x(t,e)+f(t),                                  (1)

x(t₀,e)=x⁰,                                             (2)

где:  A(t)  –  квадратная  матрица-функция  второго  порядка  с  элементами  а_jk(t),  f(t)=colon{f₁(t),f₂(t)}, 

а_jk(t),  f_k(t)  –  аналитические  функции  в  D, 

x⁰=colon{x₁⁰,x₂⁰}  –  постоянный  вектор,  tÎD,  t=t₁+it₂. 

U₁.  Пусть  матрица-функция  A(t)  имеет  комплексно-сопряженные  собственные  значения  l₁,₂(t)=sint±iacost,  a>1,  и  t₀=  –p/2.

U₂.  Пусть  f₁(–p/2,  –a)¹0,  f₁(p/2,  –a)¹0,  f₂(–p/2,a)¹0,  f₂(p/2,a)¹0.

В  рассматриваемом  случае  каждое  собственное  значение  имеет  по  две  простых  периодических  нулей  в  комплексной  плоскости.  Исследуемая  область  является  прямоугольником,  и  нули  собственных  значений  матрицы-функции  A(t)  находятся  на  вершинах  этого  прямоугольника.  Такой  случай  рассматривается  впервые.  Требуется  построить  асимптотику  решения  задачи  (1)—(2)  в  области  DÉ[–p/2,  p/2],  при  e®0.

Для  приведения  A(t)  к  диагональному  виду  выполняем  следующее  преобразование:  (t)A(t)B₀(t)=D(t),  где  ,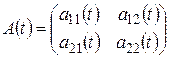 

В₀(t)=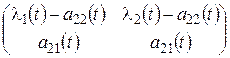,  D(t)=diag(l₁(t),  l₂(t)).

Пусть  в  области  D  выполняется  неравенство  detВ₀(t)¹0. 

Задача  (1)—(2)  с  заменой  x(t,e)=B₀(t)у(t,e)  принимает  вид:

eу'(t,e)=D(t)у(t,e)+eB(t)у(t,e)+h(t),                                   (3)

у(t₀,  e)=у⁰,                                           (4)

где  ,  ,  .

Задачу  Коши  для  дифференциальных  уравнений  (3)-(4)  заменим  интегральным  уравнением:

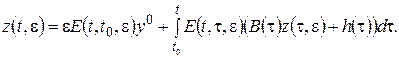  (5)

где  z(t,e)=y(t,e)e,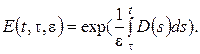 

В  работе  [4]  нами  доказана 

Теорема.  Если  для  интеграла 

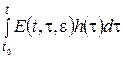,  (6)

в  некоторой  области  D  справедлива  оценка 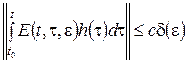 ,  где  ,  то  для  решения  системы  интегральных  уравнений  (5)  справедлива  оценка  ||z(t,e)||£cd(e).

Значит,  достаточно  вычислить  асимптотику  интеграла  (6),  при  условиях  U₁  и  U₂.  Рассмотрим  собственные  значения

Re(l₁(t₁,0))=Re(l₂(t₁,0))=sint₁;  Re(l₁,₂(t₁,0))<0  –  устойчивый  интервал,  при  –p+2pk<t₁<2pk;  Re(l₁,₂(t₁,0))>0  –неустойчивый  интервал,  при  2pk<t₁<p+2pk; 

Re(l₁,₂(t₁,0))=0,  при  t₁=pk,  kÎZ.

Отметим,  что  (p/2+pk,–a)  и  (p/2+pk,a),  где 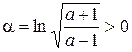   kÎZ,  являются  нулями  собственных  значений  l₁(t₁,t₂)  и  l₂(t₁,t₂)  соответственно.

Рассмотрим  теперь  функции:  u₁(t)=òl₁(t)dt,  u₂(t)=òl₂(t)dt.

Если  t=t₁+it₂,  то  u₁(t₁,t₂)=  –cost₁(cht₂+asht₂)+isint₁(sht₂+acht₂),  u₂(t₁,t₂)=

–cost₁(cht₂–asht₂)+isint₁(acht₂–sht₂).  Пусть  u₁₁(t₁,t₂)=Re(u₁(t₁,t₂)),  u₂₁(t₁,t₂)=Re(u₂(t₁,t₂)).  Область  D={t:  u₁₁(t₁,t₂)£0,  u₂₁(t₁,t₂)£0,  |t₁|£p/2}  –  является  прямоугольником  с  вершинами  A(–p/2,–a),  B(p/2,–a),  B₁(p/2,a)  и  A₁(–p/2,a). 

Решение  предельной  (вырожденной)  системы:  (t)=  –A^-1(t)f(t)  в  четырех  точках  A(–p/2,–a),  B(p/2,–a),  B₁(p/2,a)  и  A₁(–p/2,a)  имеет  особенность,  при  f(t)¹0.  Кроме  того  это  решение  не  удовлетворяет  начальному  условию  (t₀)¹x⁰.

Таким  образом,  мы  здесь  тоже  сталкиваемся  с  двумя  сингулярностью:  первое  это  наличие  пограничного  слоя,  а  второе  —  соответствующее  невозмущенное  (предельное)  уравнение  имеет  особенность  в  точках  A(–p/2,–a),  B(p/2,–a),  B₁(p/2,a)  и  A₁(–p/2,a).  Каждое  уравнение  системы  (1)  имеет  по  две  точки  поворота,  в  целом  система  имеет  четыре  точек  поворота.  Поэтому  рассматриваемую  задачу  можно  называть  бисингулярной.

Перейдем  к  оценке  интегралов

,

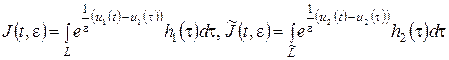где:  L,    —  пути  интегрирования,  соединяющие  точки  (–p/2,0)  и  tÎD.  Пути  интегрирования  L,    симметричны  относительно  действительной  оси.  Область  D  разобьём  на  подобласти:

Н₀₀={t:  0£t₁+p/2£d,  d£t₂+a£2a},  Н₁₀={t:0£t₁+p/2£de^g,  t₂+a=de^g},

Н₀₁={t:–p/2+d£t₁,  u₁₁(t₁,t₂)£(elne)/2,  d£|(t₁–p/2)+i(t₂+a)|,  t₂£a},

Н₁₁={t:–((1–2g)elne)/2£t₂+a£de^g_,  t₁+p/2=de^g},

Н₁₂={t:  |t₁|£p/2–de^g_,  u₁₁(t₁,t₂)=((1–2g)elne)/2},

Н₁₃={t:–((1–2g)elne)/2£t₂+a£de^g_,  t₁=p/2–de^g},

Н₁₄={t:–  de^g£t₁–p/2£((1–2g)elne)/2,  t₂+a=de^g},

Н₁₅={t:  u₁₁(t₁,t₂)=((1–2g)elne)/2,  de^g£t₂+a£2a},

Н₂₀={t:0£t₁+p/2£d,  0£t₂+a£d},  Н₂₁={t:  |t₁|£p/2–d,  (elne)/2£u₁₁(t₁,t₂)  £0},

Н₂₂={t:–d£t₁–p/2£0,  (elne)/2£u₁₁(t₁,t₂)£0},  0<d<<1  —  достаточное  малое  число,  0£g<1/2,  Н₀=Н₀₀ÈН₀₁,  Н₁=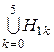,  Н₂=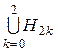,  D=Н₀ÈН₁ÈН₂.

Лемма  1.  Если  tÎH₀₀,  то  для  интеграла  J(t,e)  справедлива  оценка

|J(t,e)|£ce.                 (7)

Доказательство.  Путь  интегрирования  L  состоит  из  отрезка  прямой  t₂=(t₁–t₀)t₂/(t₁–t₀),  соединяющей  точки  (t₀,0)  и  tÎН₀₀.  Так  как  в  области  Н₀₀  имеет  место  условие:  Re(l₁(t₁,t₂))=sint₁(cht₂+asht₂)£–c<0,  то  имеем: 

.

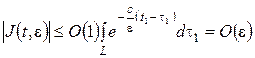Справедливость  этой  оценки  также  можно  доказать  и  интегрируя  по  частям  J(t,e).  ¨

Лемма  2.  Если  tÎH₁₀,  то  для  интеграла  J(t,e)  справедлива  оценка

|J(t,e)|£ce^1–g,  где  0£g<1/2.                                     (8)

Доказательство.  Путь  интегрирования  L  тот  же  что  в  лемме  1.  Интегрируя  J(t,e)  по  частям  имеем:  |J(t,e)|£e|h₁(t)/l₁(t)|+O(e).

Учитывая,  что  l₁(t)=O((t+p/2+ia))  и  сe^g£|l₁(t)|£Ce^g,  то  следует  оценка: 

|eh₁(t)/l₁(t)|=O(e^1–g).¨

Рассмотрим  следующий  интеграл

,

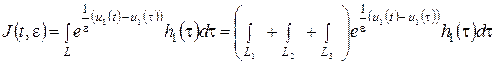где:  L=L₁ÈL₂ÈL₃,  J(t,e)=j₁(t,e)+j₂(t,e)+j₃(t,e), 

L₁  —  отрезок  линии  t₁=–p/2,  –a£t₂£0; 

L₂  —  отрезок  линии  t₂=  –a,  –p/2£t₁£t₁; 

L₃  —  отрезок  линии  t₁=t₁,  –a£t₁£t₂;

Вычисляя  эти  интегралы,  получим  оценки:

;  (9)

;  (10)

1.  Пусть  –p/2£t₁£–p/2+de^1/2,  0£t₂+a£de^1/2,  тогда  |j₃(t,e)|£ce^1/2.        (11)

2.  Пусть  |t₁|£p/2–de^1/2,  тогда  |j₃(t,e)|£ce.              (12)

3.  Пусть  p/2–de^1/2£t₁£p/2,  0£t₂+a£de^1/2,  тогда  |j₃(t,e)|£ce^1/2.                     (13)

4.  Пусть  p/2–de^1/2£t₁£p/2,  de^1/2£t₂+a£2a,  тогда

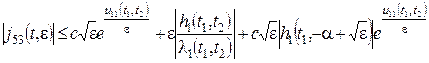.                    (14)

Из  этих  оценок  следует  справедливость  следующих  лемм.

Лемма  3.  Если  tÎH₂₀ÈH₂₁ÈH₂₂,  то  для  интеграла  J(t,e)  справедлива  оценка:  |J(t,e)|£ce^1/2.

Доказательство  следует  из  (9)—(11),  (13),  (14).

Лемма  4.  Если  tÎH₁₂ÈH₁₃ÈH₁₄ÈH₁₅,  то  для  J(t,e)  справедлива  оценка:

|J(t,e)|£ce^1–g.

Доказательство  следует  из  (9),  (10),  (12),  (14).

Лемма  5.  Если  tÎH₀₁,  то  для  J(t,e)  справедлива  оценка:  |J(t,e)|£ce.

Доказательство  следует  из  (9),  (10),  (12),  (14).

Следовательно,  справедлива 

Теорема.  Пусть  выполняются  условия  U₁,  U₂.  Тогда  задача  (1)-(2)  имеет  единственное  решение  и  для  него  справедлива  асимптотическая  оценка:

,

где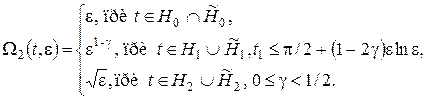 

Список  литературы:

1.Алыбаев  К.С.  Метод  линий  уровня  исследования  сингулярно  возмущенных  уравнений  при  нарушении  условия  устойчивости:  Дис.  …  д-ра  физ.-мат.  наук:  01.01.02.  Жалалабат,  2001.  —  203  с.

2.Нейштадт  А.И.  Асимптотическое  исследование  потери  устойчивости  равновесия  при  медленном  прохождении  пары  собственных  чисел  через  мнимую  ось  //  Успехи  мат.  наук.  —  1985.  —  Т.  40,  —  Вып.  5.  —  С.  300—301.

3.Турсунов  Д.А.  Асимптотика  решений  сингулярно  возмущенных  уравнений  в  случае  смены  устойчивости,  когда  собственные  значения  имеют  n-кратный  полюс:  Дис.  …  канд.  физ.-мат.  наук:  01.01.02.  Ош,  2005.  —  110  с.

4.Турсунов  Д.А.  Асимптотика  решения  сингулярно  возмущенной  задачи  с  периодической  точкой  поворота  //  интернет  журнал  ВАК  КР.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://195.38.189.154:81/jurnal/  (дата  обращения  27.08.2013).