Статья опубликована в рамках: XI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 14 октября 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОБЪЕКТНО-ОРИЕНТИРОВАННЫЙ ПОДХОД В МАТЕМАТИЧЕСКОМ АНАЛИЗЕ
Богун Виталий Викторович
канд. пед. наук, доцент кафедры математического анализа Ярославского государственного педагогического университета им. К.Д. Ушинского, г. Ярославль
THE OBJECT-ORIENTED APPROACH IN THE MATHEMATICAL ANALYSIS
Vitaly Bogun
candidate of Science, assistant professor of chair of the mathematical analysis of the Yaroslavl state pedagogical university of K.D.Ushinsky, Yaroslavl
АННОТАЦИЯ
Рассмотрено применение объектно-ориентированного подхода в программировании применительно к информатике и в рамках математического анализа с точки зрения математики. Представлены детальное описание алгоритма работы программы и нахождение интегралов с точки зрения объектно-ориентированного подхода.
ABSTRACT
Application of the object-oriented approach in programming with reference to computer science and within the limits of the mathematical analysis from the point of view of mathematics is considered. The detailed description of algorithm of work of the program and a finding of integrals from the point of view of the object-oriented approach are presented.
Ключевые слова: объектно-ориентированный подход; программирование; математический анализ.
Keywords: The object-oriented approach; programming; the mathematical analysis.
В настоящее время при информационном рассмотрении любого изучаемого процесса или явления применяется объектно-ориентированный подход (ООП), суть которого заключается в разделении рассматриваемого конечного множества объектов, которые выделяются в результате моделирования данного процесса в силу их существенного влияния на процесс или явление, на определенное количество классов объектов. Все объекты в рамках одного класса обладают единым строго определенным набором статических свойств (атрибутов), характеризующих существенные признаки объектов, и динамических свойств (событий, являющихся реакциями на реализуемые действия), характеризующих поведение объектов. Объекты в рамках одного класса могут различаться или совпадать в плане значений атрибутов или алгоритмами, а также результатами реализации событий [6, 4].
С точки зрения информационных процессов можно рассмотреть реализацию объектно-ориентированного подхода применительно к решению задачи по расчету и выводу результатов сложения и умножения двух вводимых пользователем целых чисел (рис. 1).
Как видно из рисунка, можно выделить три класса объектов в рамках программы (текстовые надписи, текстовые поля и кнопки), для которых в таблице 1 указаны статические и динамические свойства.
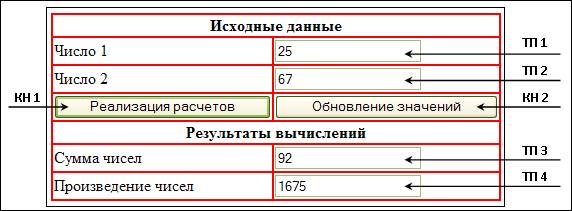
Рисунок 1. Реализация объектно-ориентированного подхода при решении информационной задачи
Таблица 1.
Описание статических и динамических свойств объектов в рамках информационной задачи
|
Классы объектов |
|||||
|
Класс 1 «Текстовые поля» |
Класс 2 «Кнопки» |
||||
|
Объект 1 (ТП 1) |
Объект 2 (ТП 2) |
Объект 3 (ТП 3) |
Объект 4 (ТП 4) |
Объект 1 (КН 1) |
Объект 2 (КН 2) |
|
Статические свойства (атрибуты) |
|||||
|
Атрибут 1: Тип объекта Атрибут 2: Имя объекта |
Атрибут 1: Тип объекта Атрибут 2: Значение надписи на кнопке |
||||
|
Динамические свойства (действия) |
|||||
|
Действия не являются необходимыми |
Действие 1: Нажатие на кнопку (обработка события) |
||||
|
Механизмы для реализации динамических свойств (действий) |
|||||
|
Отсутствует необходимость применения событий |
|
|
|||
Алгоритм работы программы заключается в том, что при указании значений исходных данных в текстовых полях формы (ТП 1 и ТП 2) и последующем нажатии кнопки реализации расчетов (КН 1) благодаря применению соответствующей функции для комплексной обработки информации осуществляется получение исходных данных из текстовых полей, расчет суммы и произведения чисел и вывод результатов расчетов также в соответствующие поля формы (ТП 2 и ТП 4). При активации кнопки обновления значений (КН 2) осуществляется изменение значений в текстовых полях формы до значений по умолчанию.
Однако объектно-ориентированный подход можно применить и при решении задач по математике в общем и математическому анализу в частности. Например, при рассмотрении раздела «Интегрирование функций» в математическом анализе можно всё множество интегралов свести к определенному количеству классов объектов: неопределенные, определенные, собственные и несобственные интегралы [1, 4—6].
В данном случае интегралы можно представить классификацию интегралов по статическим (например, неопределенные и определенные интегралы) и динамическим свойствам, отражающихся в применении определенных операций над интегралами определенного класса, что отражено в таблице 2.
Таблица 2.
Применение объектно-ориентированного подхода к интегралам
|
Классы объектов |
|||
|
Класс 1 «Неопределенные интегралы» |
Класс 2 «Определенные интегралы» |
||
|
Объект 1 (Интеграл 1)
|
Объект 2 (Интеграл 2)
|
Объект 1 (Интеграл 1)
|
Объект 2 (Интеграл 2)
|
|
Статические свойства (атрибуты) |
|||
|
Атрибут 1: Наименование переменной интегрирования. Атрибут 2: Выражение подинтегральной функции
|
Атрибут 1: Наименование переменной интегрирования. Атрибут 2: Выражение подинтегральной функции Атрибут 3: Значение нижнего предела интегрирования Атрибут 4: Значение нижнего предела интегрирования |
||
|
Динамические свойства (действия) |
|||
|
Действие 1: Нахождение неопределенного интеграла с применением различных методов |
Действие 1: Нахождение неопределенного интеграла с применением различных методов Действие 2: Подстановка значений верхнего и нижнего пределов интегрирования |
||
Таким образом, в рамках как информационных технологий при реализации программирования различных, так и при рассмотрении решения математических задач в рамках математического анализа, может применяется объектно-ориентированный подход, который позволяет четко разложить исследуемый процесс с точки зрения конечного множества объектов в рамках задачи на классы объектов с обозначенными статическими и динамическим свойствами.
Список литературы:
1.Богун В.В., Смирнов Е.И. Лабораторный практикум с графическим калькулятором [Текст]: учеб. пособие. Ярославль: Изд-во «Канцлер», 2010. — 272 с.
2.Веллинг, Люк, Томсон, Лора. Разработка Web-приложений с помощью PHP и MySQL, 2-е издание.: Пер. с англ. [Текст]: М.: Издательский дом «Вильямс», 2003. — 800 с.: ил. — Парал. тит. англ.
3.Выгодский М.Я. Справочник по высшей математике [Текст] М.: ООО «Большая Медведица», 2001 — 864 с.
4.Ермаков В.И. Общий курс высшей математики для экономистов [Текст] / В.И. Ермаков. М.: Инфра-М, 2008. — 656 с.
5.Кожухов И.Б., Прокофьев А.А. Справочник по математике [Текст] М.: «Лист», 1999. — 640 с.
6.Колисниченко Д.Н. Самоучитель PHP 5 [Текст]: СПб.: Наука и техника, 2007. — 640 с., ил.
дипломов


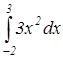
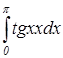
Оставить комментарий