АЛГОРИТМ  РЕКОНФИГУРАЦИИ  РАСПРЕДЕЛЕННОЙ  ИНФОРМАЦИОННО-УПРАВЛЯЮЩЕЙ  СИСТЕМЫ  В  УСЛОВИЯХ  ДЕФИЦИТА  ВРЕМЕНИ

Клименко  Анна  Борисовна

канд.  техн.  наук,  младший  научный  сотрудник,  научно-исследовательский  институт  многопроцессорных  вычислительных  систем  имени  академика  А.В.  Каляева  федерального  государственного  автономного  образовательного  учреждения  высшего  профессионального  образования  «Южный  федеральный  университет»,  г.  Таганрог

E-mail: 

Мельник  Эдуард  Всеволодович

канд.  техн.  наук,  заведующий  лабораторией,  научно-исследовательский  институт  многопроцессорных  вычислительных  систем  имени  академика  А.В.  Каляева  федерального  государственного  автономного  образовательного  учреждения  высшего  профессионального  образования  «Южный  федеральный  университет»

DISTRIBUTED  INFORMATIONAL  CONTROL  SYSTEM  RECONFIGURATION  ALGORITHM  IN  THE  LACK  OF  TIME  CONDITIONS

Klimenko  Anna  Borisovna

ph.D  in  Computer  science,  junior  research  fellow,  SFedU  Acad.  Kalyaev  Scientific  Research  Institute  of  Multiprocessor  Computer  Systems,  Taganrog

Melnik  Edward  Vsevolodovich

ph.D  in  Computer  science,  Head  of  Laboratory,  SFedU  Acad.  Kalyaev  Scientific  Research  Institute  of  Multiprocessor  Computer  Systems,  Taganrog

АННОТАЦИЯ

Статья  посвящена  вопросам  реконфигурирования  РИУС  в  условиях  дефицита  времени.  Приводится  математическая  модель  задачи,  на  примере  адаптированного  алгоритма  имитации  отжига  показана  возможность  сокращения  времени  получения  решения. 

ABSTRACT

The  paper  is  devoted  to  the  DICS  reconfiguration  in  the  lack  of  time  conditions  questions.  The  mathematical  model  of  task  is  presented.  Also,  by  presented  example  of  adapted  simulated  annealing  algorithm,  the  possibility  of  the  decision  calculating  time  reducing  is  shown.

Ключевые  слова:  параллельные  вычисления;  информационно-управляющая  система;  реконфигурация;  восстановление;  имитация  отжига.

Keywords:  parallel  computing;  informational-control  system;  reconfiguration;  recovery;  simulated  annealing.

Информационно-управляющие  системы  (ИУС)  применяются  практически  повсеместно,  начиная  от  бытовой  техники  и  заканчивая  комплексными  объектами  атомной  энергетики  и  авиационной  техники.  В  общем  случае  ИУС  определяется  как  цифровая  система  контроля  или  управления  некоторым  реальным  объектом,  а  основным  ее  отличием  от  универсальной  вычислительной  системы  является  то,  что  ИУС  решаются  задачи,  связанные  с  необходимостью  принятия  решения  в  реальном  времени. 

Если  вести  речь  о  современных  ИУС,  то  их  классифицируют  по  различным  признакам.  Например,  одним  из  часто  используемых  признаков  классификации  является  критичность  возникновения  ошибки  на  объекте,  находящемся  под  управлением  ИУС.  Выделяют  следующие  основные  классы  объектов  [4]:

·     возникновение  ошибки  некритично  и  не  влечет  за  собой  сколь-нибудь  значимые  последствия,  при  этом  доступ  к  объекту  не  затруднен  (бытовая  и  офисная  техника);

·     возникновение  ошибки  не  приводит  к  значимым  последствиям,  однако  объект  эксплуатируется  в  условиях  невозможности  своевременного  доступа  и  проведения  ремонтных  работ  (искусственные  спутники  Земли);

·     возникновение  ошибки  в  управлении  объектом  может  привести  к  серьезным  последствиям:  человеческим  жертвам,  техногенным  катастрофам  и  т.  п.  (авиационная  техника,  объекты  атомной  энергетики,  ТЭС,  ГЭС  и  прочее).

Необходимость  обеспечения  должной  степени  отказоустойчивости  и  надежности  ИУС  двух  последних  классов  объектов  акцентировала  внимание  на  разработке  соответствующих  ИУС.  Рассмотрим  кратко  архитектуры  ИУС  [4].  В  настоящее  время  до  сих  пор  одной  из  самых  используемых  является  централизованная  архитектура  ИУС  (рис.  1).

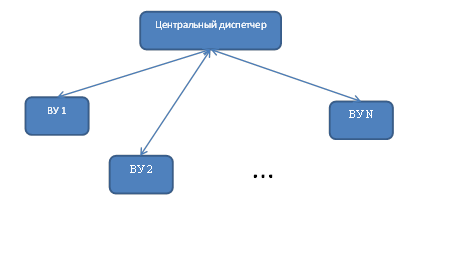
Рисунок  1.  Централизованная  архитектура  ИУС

Недостатки  такой  архитектуры  вполне  очевидны:  в  случае  отказа  ВУ,  на  котором  расположен  центральный  диспетчер,  который  распределяет  подзадачи  по  подчиненным  ВУ,  система  полностью  утрачивает  работоспособность.  Дублирование  центрального  диспетчера  также  не  всегда  допустимо,  например,  при  жестких  требованиях  к  массо-габаритным  показателям  аппаратного  комплекса.  Альтернативным  решением  является  иерархическая  архитектура  (рис.  2),  функционирование  которой  подробно  изложено  в  работах  [2,  3].

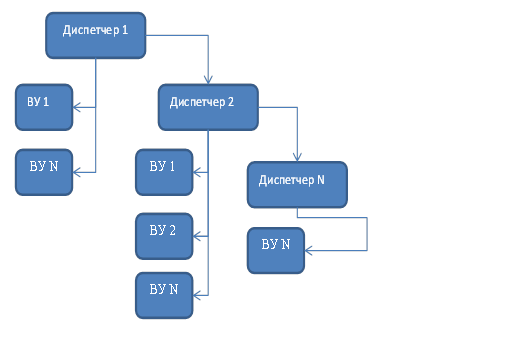
Рисунок  2.  Иерархическая  архитектура  ИУС

Предполагается,  что  в  случае  отказа  одного  из  диспетчеров,  его  задачи  на  себя  принимает  дочерний  узел.  Однако  такой  подход  к  построению  ИУС  влечет  немало  проблем  реализации,  таких,  например,  как  способ  выбора  «замещающего»  диспетчера,  передача  контекста  выполняемой  подзадачи,  возвращение  диспетчера  к  работе  после  восстановления  и  т.  п.

Еще  одним  типом  архитектуры  ИУС  является  децентрализованная  (распределенная).  Распределенная  ИУС  (РИУС)  подразумевает  следующее:  в  систему  объединяются  равноправные  однотипные  ВУ  с  унифицированным  программным  обеспечением,  как  показано  на  схеме  рис.  3.

Рисунок  3.  распределенная  архитектура  ИУС

Последняя  архитектура  считается  наиболее  перспективной  в  аспектах  надежности  и  способности  к  восстановлению  после  сбоев  [4].

Процесс  восстановления  после  происшедшего  сбоя  и  выхода  из  строя  одного  и  более  ВУ,  иными  словами  —  реконфигурация  —  является  одним  из  важнейших  процессов  РИУС.  Задача  реконфигурации  в  общем  виде  заключается  в  перераспределении  тех  подзадач,  которые  должны  были  решаться  на  вышедших  из  строя  узлах,  на  функционирующие  ВУ  при  условии,  что  ЗУ  будет  решена  в  ранее  установленные  сроки.  Последнее  условие  особенно  актуально  для  РИУС,  разрабатываемых  для  авиации,  поскольку  решение  ЗУ  полученное  бортовой  ИУС  позже  оговоренного  момента  времени,  может  оказаться  бесполезным.  С  другой  стороны,  задача  реконфигурации  относится  к  классу  NP-полных,  что  само  по  себе  делает  весьма  затруднительным  ее  решение  в  сжатые  сроки.

Проблемы  планирования  выполнения  работ  и  составление  расписаний  широко  и  неоднократно  освещались  в  работах  российских  и  зарубежных  ученых,  начиная  с  60-х.  Тем  не  менее,  необходимо  отметить  работы  А.Б.  Барского,  сформулировавшего  задачу  формирования  комплектации  неоднородной  вычислительной  системы  минимальной  стоимости  и  предложившего  аналитический  метод  ее  решения,  состоящий  в  комбинировании  метода  «ветвей  и  границ»  с  полным  перебором  возможных  вариантов  решения  в  пределах  выделенных  «ветвей»  [1]. 

В  качестве  модели  задачи  реконфигурации  примем  следующую,  допуская  идеальность  КС:

1.  Информационный  граф  без  циклов,  описывающий  задачу  управления  и  разбитый  на  подзадачи,  которые  требуется  распределить  по  ПУ:

G=(H,X,W),                                                           (1)

где:  H={j}={1,…,n}  —  вершины  графа,

X={x_j}  —  предварительно  оцененные  трудоемкости  задач,

W  —  множество  дуг,  определяющих  связи  между  задачами  по  информации,  каждая  из  которых  взвешена  значением  w_kl,  которое  определяет  объем  передаваемых  данных  между  k-ой  и  l-ой  задачами.

2.  Неоднородное  множество  ПУ  M={m_i},  i=1,…k, 

                                           m_i=<i,  prod_i,  v_i,  s_i>,                                  (2)

где:  i  —  порядковый  номер  ПУ,

  —  производительность  ПУ, 

  —  стоимость  ПУ;

  —  скорость  передачи  результата  вычислений  (решения  задачи)  в  коммутационную  среду  (КС),  которая  считается  полносвязной. 

3.  Резервное  множество  ПУ  M_avail,  где  каждое  m_k  описывается  кортежем  (2). 

4.  Максимально  допустимое  время  решения  задачи  T_plan.

5.  Также  обозначим  фактическое  время  решения  задачи,  описанной  информационным  графом  G  через  T_c. 

Оценка  равномерности  распределения  нагрузки,  необходимость  которой  отмечена  в  [4],  вычисляется  следующим  образом: 

·     определяется  идеальная  нагрузка  на  ПУ  путем  деления  суммы  трудоемкостей  подзадач  на  количество  ПУ;

·     после  построения  расписания  выполнения  подзадач  каждому  ПУ  назначено  некоторое  их  подмножество.  Трудоемкости  подмножества  закрепленных  за  ПУ  задач  суммируются;

·     производится  их  сравнение  с  идеальной  загрузкой  ПУ,  вычисленной  ранее.

Формально  оценку  равномерности  распределения  нагрузки  на  ПУ  опишем  следующими  формулами  (3,4,5):

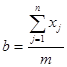,                                            (3)

где:  b  —  идеальная  в  аспекте  равномерности  распределения  нагрузка  на  ПУ;

x_j  —  трудоемкость  j-й  подзадачи;

n  —  количество  подзадач,

m  —  количество  процессорных  устройств.

,                                            (4)

где:  b_i  —  фактическая  нагрузка  на  ПУ,  определяемая  суммированием  назначенных  ему  на  решение  подзадач.

Выражение  (5)  определяет  оценку  равномерности  распределения  нагрузки  на  ПУ  и  в  идеальном  случае  равна  1.

                                       (5)

Учитывая,  что  на  практике  получение  B=1  представляется  маловероятным,  имеет  смысл  ввести  величину,  определяющую  допустимое  отклонение  по  распределению  нагрузки,  например,  .      

Таким  образом,  формально  задача  может  быть  представлена  в  следующем  виде:

среди  множества  вариантов  комплектаций  системы  ПУ  K={k₁,…k_q}  с  соответствующими  стоимостями  комплектации  S={s₁,…s_q}  с  исходными  данными,  перечисленными  в  п.п.  1-5  необходимо  найти    и  план  распределения  задач  по  ПУ  при  выполнении  следующих  условий:

·        ;                                                     (6)

·                                                      (7)

·        .                                            (8)

Метод  решения  задачи  о  нахождении  комплектации  неоднородной  ВС  минимальной  стоимости,  предложенный  А.Б.  Барским,  позволяет  получить  точное  решение,  но  при  этом  автор  делает  оговорку,  что  решение  задачи  может  занимать  длительное  время  [1].  Вполне  очевидно,  что  по  этой  причине  для  процесса  реконфигурации  подобный  метод  решения  неприменим. 

Помимо  точных  методов  решения  подобных  задач  комбинаторной  оптимизации  в  настоящее  время  часто  используются  численные  методы,  такие,  как  алгоритмы  имитации  отжига  и  генетические  алгоритмы,  основным  достоинством  которых  считается  возможность  получения  оптимального  решения  (или  субоптимального)  за  приемлемое  время,  а  среди  общих  недостатков  выделяют  зависимость  скорости  получения  решения  от  настройки  параметров.

Однако,  говоря  о  РИУС  как  о  системе  равноправных  ВУ,  находящихся  под  управлением  локальных  диспетчеров,  необходимо  отметить  следующее:  метод  получения  конфигурации  РИУС  должен  быть  ориентирован  на  его  параллельное  выполнение  равноправными  ВУ,  что  делает  актуальной  адаптацию  известных  методов  решения  задачи  получения  конфигурации  РИУС  к  условиям  параллельного  выполнения  с  акцентом  на  сокращении  времени  получения  решения.

Метод  имитации  отжига  является  в  общем  случае  итерационным  и  последовательным,  что  в  некотором  смысле  затрудняет  его  распараллеливание.  Тем  не  менее,  были  разработаны  и  используются  следующие  способы  организации  параллельного  поиска  решений  [5,  6].

1.  Параллельный  запуск  алгоритма  имитации  отжига;

2.  Параллельный  запуск  алгоритма  имитации  отжига  с  обменом  результатами;

3.  Разбиение  пространства  решений  на  области.

Первый  способ  —  параллельный  запуск  алгоритма  имитации  отжига  —  предполагает  вычисление  глобального  минимума  целевой  функции  одновременно  на  нескольких  ВУ  с  последующим  выбором  лучшего  решения  управляющим  узлом.

Второй  способ  —  параллельный  запуск  алгоритма  с  обменом  результатами  —  предполагает  по  истечении  определенного  количества  итераций  обмен  между  ВУ  и  выбор  лучшего  результата  для  продолжения  вычислений.

Третий  способ  —  разбиение  пространства  решений  на  области  —  предполагает  запуск  последовательного  алгоритма  имитации  отжига  в  каждой  из  выделенных  областей  решений  с  выбором  наилучшего  решения  по  окончании  вычислений.

Рассмотрим  один  из  возможных  вариантов  адаптации  алгоритма  для  реконфигурирования  РИУС,  ориентированная  на  выполнение  системой  равноправных  ВУ.

Схема  метода  имитации  отжига  задается  следующими  параметрами  [5]:

·     выбором  шага  изменения  температуры  T(k)  где  k  —  номер  шага;

·       выбором  порождающего  семейства  распределений  F(x,T),  где  x  —  вектор  решения,  T  —  температура  системы;

·     выбором  функции  вероятности  принятия  нового  состояния  h(),  где    —  изменение  энергии  системы,  T  —  температура.

Так  как  при  восстановлении  системы  после  сбоя  критичным  становится  время,  затраченное  на  решение  самой  задачи  реконфигурирования,  в  качестве  закона  изменения  температуры  целесообразно  выбрать  схему,  предложенную  Цу  и  Хартли  [5]:

      ,                                     (9)

где:    —  номер  шага,

  —  начальная  температура.

В  качестве  закона  выбора  нового  решения  примем  следующий:  каждый  ВУ  считает  себя  приоритетным  при  распределении  подзадач  с  нефункционирующего  ВУ,  т.  е.  пытается  в  первую  очередь  «забрать»  освободившиеся  подзадачи  себе  на  выполнение.  Для  распределения  прочих  задач  можно  воспользоваться  правилом  «каждый  ВУ  получает  на  выполнение  ту  задачу,  которую  он  выполнит  быстрее».  Приведенное  правило  диспетчирования  используется  в  алгоритме  диспетчеризации  для  неоднородной  ВС  в  работе  [1]  и  гарантирует  минимизацию  времени  выполнения  графа  подзадач.  «Свободные»  задачи,  которые  должны  быть  решены,  каждый  ВУ  организует  в  последовательный  список  и  перебирает  возможные  комбинации.

В  качестве  h()  используем  следующее:

.

Таким  образом,  алгоритм  формирования  конфигурации  РИУС  минимальной  стоимости  после  сбоя  будет  иметь  следующий  вид.

1.  ВУ  формирует  список  подзадач,  требующих  распределения,  случайным  образом  выбирается  начальный  вариант  распределения.  Производится  вычисление  целевой  функции  (в  данном  случае  —  стоимость  комплектации  ВУ  для  полученного  распределения).

2.  Произвести  сравнение  энергии  системы  E  в  состоянии  x  с  рассчитанным  глобальным  минимумом.  Если  значение  целевой  функции  меньше,  то  изменить  значение  текущего  глобального  минимума.

3.  Выбирая  подзадачи  из  сформированного  списка,  сформировать  новое  распределение  задач.

4.  Вычислить  значение  целевой  функции.  Если  полученное  значение  времени  удовлетворяет  ограничению  (6),  то  проверить  ограничения  (7,8).  Если  все  ограничения  удовлетворены,  то  считаем  решение  найденным,  перейти  к  п.  5.  В  противном  случае:  вычислить  вероятность  перехода  системы  в  новое  состояние.  В  зависимости  от  результата,  перейти  на  новую  итерацию  (п.  2),  либо  к  п.  3.

5.  Выставить  полученное  решение  в  коммутационную  среду,  разослать  сообщение  об  окончании  вычислений.

6.  Если  получено  сообщение  об  окончании  вычислений,  выставить  в  коммутационную  среду  значение  текущего  глобального  минимума.

7.  Выбрать  посредством  общего  голосования  из  представленных  в  КС  вариантов  решений  лучшее,  принять  его  для  выполнения.

Приведенный  пример  адаптированного  алгоритма  имитации  отжига  обладает  следующими  особенностями:  во-первых,  так  как  критично  время  нахождения  удовлетворительного  решения,  речь  идет  не  о  поиске  глобального  минимума,  а  о  нахождении  первого  подходящего  решения.  Как  только  ВУ  находит  такое  решение,  в  КС  выставляется  сигнал  о  прекращении  вычислений.  Прочие  ВУ  также  выставляют  полученные  на  текущий  момент  решения,  из  них  совместно  выбирается  лучшее  по  значению  целевой  функции. 

Реализация  приведенного  адаптированного  алгоритма  в  виде  программной  модели  позволяет  сделать  некоторые  предварительные  выводы  о  перспективности  его  использования.  При  исходном  размере  произвольного  графа  задачи  управления  в  7000  подзадач  равной  трудоемкости,  при  увеличении  числа  ВУ  в  программной  модели  происходит  сокращение  времени  (в  условных  единицах  времени  моделирования)  поиска  подходящих  решений,  качество  которых  удовлетворяет  установленным  ограничениям,  как  показано  на  рис.  4.  На  графике  красным  цветом  показаны  результаты  работы  параллельного  поиска  решения  без  останова  по  достижению  удовлетворительного  результата  одним  из  ВУ,  синим  цветом  выделены  результаты  работы  описанного  в  статье  алгоритма. 

Результат  работы  алгоритма  в  смысле  тенденции  уменьшения  времени  поиска  решения  является  ожидаемым,  поскольку  с  увеличением  количества  попыток  поиска  оптимального  решения  в  условиях  распараллеливания  алгоритма  по  ВУ  при  генерации  различных  начальных  точек  повышается  вероятность  более  «быстрого»  обнаружения  решения.  Аналогично  ожидаемым  является  сокращение  времени  поиска  по  сравнению  с  параллельным  запуском  алгоритма  имитации  отжига  без  участия  ВУ  в  выборе  момента  останова.  При  этом,  очевидно,  качество  найденного  решения  может  быть  хуже,  но  в  условиях  принятых  допущений  о  том,  что  нас  устроит  любое  как  можно  скорее  найденное  решение,  ухудшение  качества  решения  допустимо.  При  дальнейшем  увеличении  количества  ВУ  на  времени  выполнения  алгоритма  начинают  сказываться  накладные  расходы  на  коммуникацию  между  ВУ  и  на  сравнение  выставленных  в  КС  результатов  вычислений.

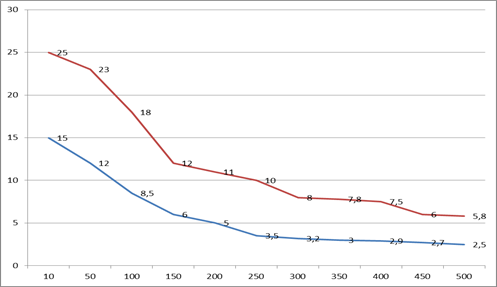
Рисунок  4.  Результаты  программного  моделирования  работы  алгоритма

Список  литературы:

1.Барский  А.Б.  Параллельные  процессы  в  вычислительных  системах:  планирование  и  организация.  —  М.:  Радио  и  связь,  1990.

2.Дьячков  В.А.,  Захаров  В.Н.,  Козмидиади  В.А.,  Кузьмин  А.В.,  Шулятников  Д.С.  Алгоритмы  параллельного  выполнения  заданий  сервисных  приложений  в  распределенной  среде.  //Системы  и  средства  информатики/Ин-т  проблем  информатики  РАН.  —  М.:  Наука,  2008.  321  с.

3.Захаров  В.Н.,  Козмидиади  В.А.,  Кузьмин  А.В,  Попов  А.С.,  Шулятников  Д.С.  Планирование  выполнения  зданий  сервисных  приложений  в  распределенной  среде.  //Системы  и  средства  информатики/Ин-т  проблем  информатики  РАН.  —  М.:  Наука,  2008.  321  с.

4.Каляев  И.А,  Мельник  Э.В.  Децентрализованные  системы  компьютерного  управления.  Ростов  н/Д:  Издательство  ЮНЦ  РАН,  2011.  196  с.

5.Лопатин  А.С.  Метод  отжига  //  Стохастическая  оптимизация  в  информатике.  СПб.:  Изд-во  СПбГУ,  2005.  Вып.  1.  С.  133—149.

6.Савин  А.Н.,  Тимофеева  Н.Е.  Применение  алгоритма  оптимизации  методов  имитации  отжига  на  системах  параллельных  и  распределенных  вычислений..//Известия  саратовского  университета.  Т.  12.  2012.