ДВОЙНЫЕ  И  ПОВТОРНЫЕ  ИНТЕГРАЛЫ

Корнеев  Антон  Александрович

студент  3  курса,  факультет  точных  наук  и  инновационных  технологий  МГГУ  им.  Шолохова,  г.  Москва

E-mail:  predsedatel_2012@mail.ru

Дорошкевич  Ольга  Александровна

канд.  физ.-мат.  наук,  доцент  МГГУ  им.  Шолохова,  г.  Москва

В  статье  [3]  нами  были  рассмотрены  условия  допустимости  предельного  перехода  под  знаком  интеграла  и  условия  допустимости  дифференцирования  под  знаком  интеграла.  Для  повторного  же  интеграла  рассматривать  в  качестве  параметра  переменную,  по  которой  осуществляется  внешнее  интегрирование,  не  имеет  смысла.  Интегралы  с  параметрами  можно  интегрировать  по  точкам  неравномерности,  к  примеру

1)  Рассмотрим  двойной  интеграл,  заданный  в  области 

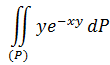
Повторные  интегралы  равны

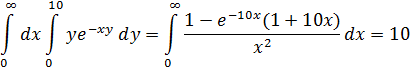
однако  предельный  переход  под  знаком  интеграла  недопустим

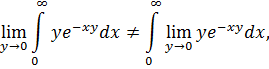
т.  к.  не  выполнено  условие  теоремы  14  [3]

2)  Рассмотрим  двойной  интеграл,  заданный  в  области 

Повторные  интегралы  равны

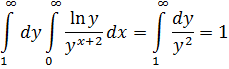
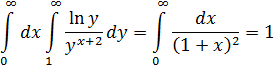
однако  предельный  переход  под  знаком  интеграла  недопустим

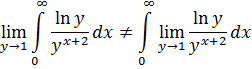
т.  к.  не  выполнено  условие  теоремы  14  [3]

Рассмотрим  более  общий  вопрос:  какого  условие  равенства  повторных  интегралов  двойному?

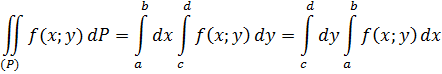
В  существующей  практике  принято  рассматривать  абсолютно  сходящиеся  двойные  и  повторные  интегралы.  Достаточным  условием  их  равенства  является  абсолютная  сходимость  последних

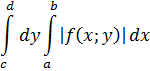
Как,  было  сказано,  данное  условие  является  достаточным,  но  не  необходимым.  Вопрос  же  о  сходимости  повторных  интегралов  к  двойному,  в  случае  их  неабсолютной  сходимости,  остается  открытым.  Повторные  интегралы  рассмотрим  со  следующей  точки  зрения:

первый  повторный  интеграл

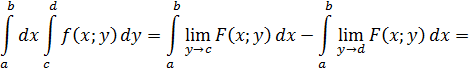
и  второй  повторный  интеграл

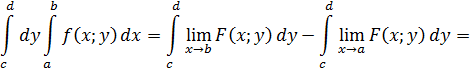
Здесь  возникает  еще  один  вопрос:  существует  ли  двойной  интеграл  и  чему  он  равен,  если  повторные  интегралы  не  равны  друг  другу? 

Как  было  показано  выше,  понятие  повторных  интегралов  тесно  связано  с  понятием  повторных  пределов.  Так  же  понятие  двойного  интеграла  связано  с  понятием  двойного  предела.  Значение  двойного  интеграла,  заданного  в  некоторой  прямоугольной  области  ,  может  быть  вычислено  непосредственно  по  следующим  формулам,  причем  даже  в  случае 

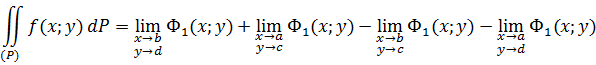
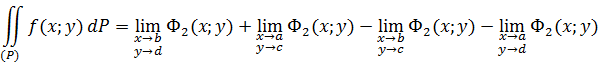
В  частности,  для  абсолютно  сходящихся  интегралов,  получаем  формулу  Ньютона-Лейбница  для  двойных  интегралов

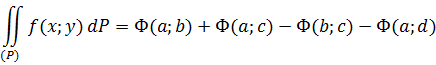
3)  Рассмотрим  двойной  несобственный  интеграл  второго  рода,  сходящийся  не  абсолютно,  заданный  в  области 

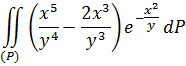
Значения  повторных  интегралов  не  равны

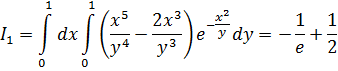
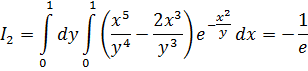
Первообразные  функции,  полученные  при  разном  порядке  интегрирования  равны  между  собой    и  равны

Непосредственно  вычисляя  двойной  интеграл  получаем

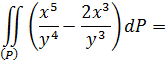
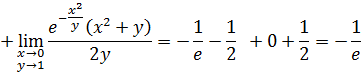
Отсюда  следует,  что  данный  двойной  интеграл  сходится  ко  второму  повторному  интегралу  .

4)  Рассмотрим  двойной  несобственный  интеграл  первого  рода,  сходящийся  не  абсолютно,  заданный  в  области 

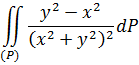
Первообразные  функции,  полученные  при  разном  порядке  интегрирования,  не  равны  между  собой 

  и    то  есть  оба  повторных  интеграла  должны  быть  равны    одновременно,  чего  на  деле  быть  не  может.  Из  неравенства  первообразных  функций    следует,  что  повторных  интегралов  не  существует.

Вычислим  значение  двойного  интеграла  непосредственно  для 

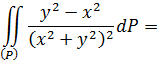
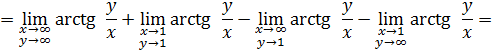
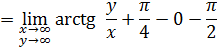
И  для 

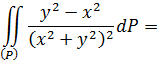
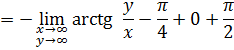
Интегрируемая  функция  кососимметрическая  [1],  поэтому  двойной  интеграл  сходится  к  нулю.  Для  обеих  первообразных  получаем 

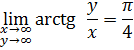
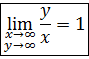
И  при  переходе  к  полярным  координатам

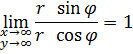
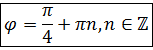
Фихтенгольцем  были  вычислены  значения  этих  повторных  интегралов  по  общему  правилу  для  абсолютно  сходящихся  интегралов  [4,  c.  739]

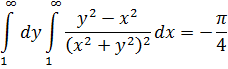
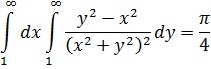
Эти  значения  им  можно  приписать  только  в  качестве  обобщенных  значений  этих  интегралов. 

Отметим  интересный  факт

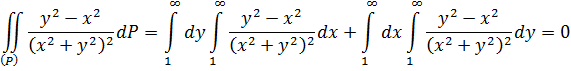
Значение  двойного  интеграла  равно  сумме  обобщенных  значений  повторных  интегралов.

5)  Рассмотрим  двойной  несобственный  интеграл  первого  рода,  сходящийся  не  абсолютно,  заданный  в  области  ,

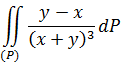
Первообразные  функции,  полученные  при  разном  порядке  интегрирования,  не  равны  между  собой 

Вычислим  значение  двойного  интеграла  непосредственно  для 

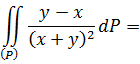
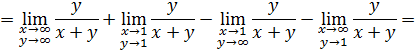
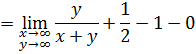
Учитывая  то,  что  интегрируемая  функция  кососимметрическая  [1],  получаем

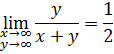
Отсюда,  переходя  к  полярным  координатам,  для    приходим  к  такому  же  результату

Список  литературы:

1.Корнеев  А.А.,  Дорошкевич  О.А.  Разложение  двойных  и  тройных  интегралов  по  бесконечным  диагоналям  //  Тенденции  развития  естественных  и  математических  наук:  мат-лы  межданар.  науч.-практ.  конф.:  28  апреля  2013  г.

2.Корнеев  А.А.,  Дорошкевич  О.А.  Теория  предельных  функций  //  Вопросы  естественных  и  математических  наук:  мат-лы  междунар.  науч.-практ.  конф.

3.Корнеев  А.А.,  Дорошкевич  О.А.  Интегралы  с  параметом  //  Вопросы  естественных  и  математических  наук:  мат-лы  междунар.  науч.-практ.  конф.

4.Фихтенгольц  Г.М.  Курс  дифференциального  и  интегрального  исчисления:  учебник:  в  3  т.  Т.  2.  —  9-е  изд.,  стер.  —  СПб.:  Лань,  2009.  —  800  с.:  ил.  —  (Учебники  для  вузов.  Специальная  книга).