ИНТЕГРАЛЫ  С  ПАРАМЕТРОМ

Корнеев  Антон  Александрович

студент  3  курса,  факультет  точных  наук  и  инновационных  технологий  МГГУ  им.  Шолохова,  г.  Москва

E-mail:  predsedatel_2012@mail.ru

Дорошкевич  Ольга  Александровна

канд.  физ.-мат.  наук,  доцент  МГГУ  им.  Шолохова,  г.  Москва

 

Вводные  замечания

Пусть    —  функция  двух  переменных,  заданная  в  некоторой  замкнутой  области  ,  где  .

Теорема  9.  Если  для  функции    существует  двойной  предел  равный  константе

 

 

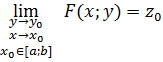
и  повторный  предел  равный  константе

 

 

то  допустим  предельный  переход

 

 

Данная  теорема,  является  следствием  теоремы  [3,  с.  361],  справедливость  которой  доказана  лишь  для  конечных    и  .  В  этой  теореме  из  равенства  двойного  и  повторного  предела  константам  следует,  что  .  В  дальнейшем  мы  убедимся,  что  теорема  9  неверна  для  бесконечных  и  . 

Предельный  переход  и  дифференцирование  под  знаком  интеграла

Следующие  теоремы  решают  вопросы,  связанные  с  допустимостью  предельного  перехода  и  дифференцирования  в  точке  под  знаком  собственных  и  несобственных  интегралов  второго  рода.  Пусть    —  функция  двух  переменных,  заданная  в  некоторой  области  ,  где  .

Теорема  10.  Если  функция    интегрируема  по    на  конечном  промежутке    и  для  её  первообразной    существуют  повторный  и  двойной  пределы  при    и    ,  где  ,  равные  константам

 

 

то  имеет  место  формула

 

 

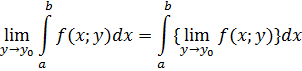
Справедливость  этой  теоремы  следует  из  справедливости  теоремы  9.

1)Проверим  допустимость  предельного  перехода  под  знаком  следующего  интеграла

 

 

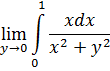
В  силу  того,  что  условия  теоремы  10  не  выполнены,  а  именно

 

 

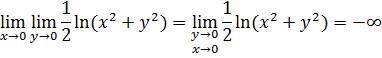
предельный  переход  под  знаком  интеграла  при    недопустим.

Теорема  11.  Если  функция    интегрируема  по    на  конечном  промежутке    и  имеет  частную  производную  по  ,  и  для  производной  её  первообразной    существуют  повторный  и  двойной  пределы  при    и    ,  где  ,  равные  константам

 

 

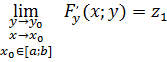
то  имеет  место  формула

 

 

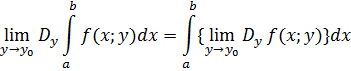
Справедливость  этой  теоремы  следует  из  справедливости  теоремы  10.

2)Проверим  допустимость  дифференцирования  под  знаком  интеграла  при 

 

 

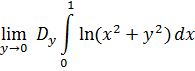
В  силу  того,  что  условия  теоремы  11  не  выполнены,  а  именно

 

 

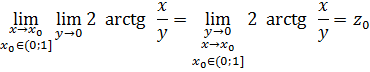
Предел

 

 

не  существует,  дифференцирование  под  знаком  интеграла  при    недопустимо.

Теорема  12.  Если  функция    интегрируема  по    на  конечном  промежутке    и  для  её  первообразной    существуют  простой  и  двойной  пределы  при    и    ,  где  ,  равные  нулю

 

 

то  имеет  место  формула

 

 

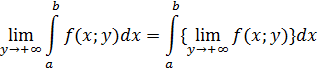
Справедливость  этой  теоремы  следует  из  справедливости  теоремы  2  [1].

3)Проверим  допустимость  предельного  перехода  при    под  знаком  следующего  интеграла

 

 

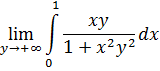
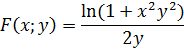
В  силу  того,  что  условия  теоремы  12  выполнены,  а  именно

 

 

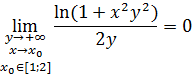
предельный  переход  под  знаком  интеграла  при    допустим.

4)Проверим  допустимость  предельного  перехода  при    под  знаком  следующего  интеграла

 

 

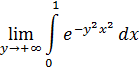
В  силу  того,  что  условия  теоремы  12  не  выполнены,  а  именно

 

 

предельный  переход  под  знаком  интеграла  при    недопустим.

Теорема  13.  Если  функция    интегрируема  по    на  конечном  промежутке    и  имеет  частную  производную  по    и  для  производной  её  первообразной    существуют  простой  и  двойной  пределы  при    и    ,  где  ,  равные  нулю

 

 

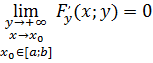
то  имеет  место  формула

 

 

Справедливость  этой  теоремы  следует  из  справедливости  теоремы  12.

Теорема  14.  Если  функция    интегрируема  по    на  бесконечном  промежутке    и  для  её  первообразной    существуют  простой  и  двойной  пределы  при    и    ,  где  ,  равные  константам

 

 

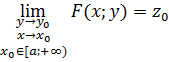
и  первообразная  как  предельная  функция  поточечно  равномерно  непрерывна  в  точке 

 

 

то  имеет  место  формула

 

 

Справедливость  этой  теоремы  следует  из  справедливости  теоремы  2  [1]  и  теоремы  9.

5)Проверим  допустимость  предельного  перехода  под  знаком  интеграла  при 

 

 

В  силу  того,  что  условия  теоремы  14  не  выполнены,  а  именно

 

 

Предел

 

 

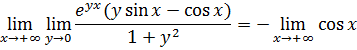
не  существует,  предельный  переход  под  знаком  интеграла  при    не  допустим.

Теорема  15.  Если  функция    интегрируема  по    на  бесконечном  промежутке    и  имеет  частную  производную  по    и  для  производной  её  первообразной    существуют  простой  и  двойной  пределы  при    и    ,  где  ,  равные  константам

 

 

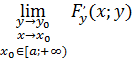
и  производная  первообразной  как  предельная  функция  равномерно  непрерывна  при 

 

 

то  имеет  место  формула

 

 

Справедливость  этой  теоремы  следует  из  справедливости  теоремы  14.

Теорема  16.  Если  функция    интегрируема  по    на  бесконечном  промежутке    и  её  первообразная    как  предельная  функция  поточечно  равномерно  непрерывна  на  этом  промежутке

 

 

то  имеет  место  формула

 

 

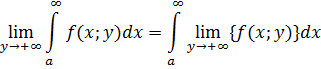
Справедливость  этой  теоремы  следует  из  справедливости  теоремы  2  [1].

6)Проверим  допустимость  предельного  перехода  под  знаком  интеграла  при 

 

 

В  силу  того,  что  условия  теоремы  16  не  выполнены

 

 

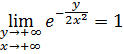
предельный  переход  под  знаком  интеграла  при    недопустим.

Теорема  17.  Если  функция    интегрируема  по    на  промежутке    и  имеет  частную  производную  по    и  производная  её  первообразной    как  предельная  функция  поточечно  равномерно  непрерывна  на  этом  промежутке

 

 

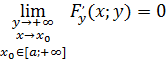
то  имеет  место  формула

 

 

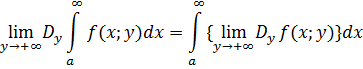
Справедливость  этой  теоремы  следует  из  справедливости  теоремы  16.

 

Список  литературы:

1.Корнеев  А.А.,  Дорошкевич  О.А.  Теория  предельных  функций  //  Вопросы  естественных  и  математических  наук:  мат-лы  междунар.  науч.-практ.  конф. 

2.Фихтенгольц  Г.М.  Курс  дифференциального  и  интегрального  исчисления:  учебник:  в  3  т.  Т.  1.  —  9-е  изд.,  стер.  —  СПб.:  Лань,  2009.  —  608  с.:  ил.  —  (Учебники  для  вузов.  Специальная  книга).