Статья опубликована в рамках: VI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 27 мая 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ТЕОРИЯ ПРЕДЕЛЬНЫХ ФУНКЦИЙ
Корнеев Антон Александрович
студент 3 курса, факультет точных наук и инновационных технологий МГГУ им. Шолохова, г. Москва
E-mail: predsedatel_2012@mail.ru
Дорошкевич Ольга Александровна
канд. физ.-мат. наук, доцент МГГУ им. Шолохова, г. Москва
Пусть ![]() — функция двух переменных, определенная на множестве
— функция двух переменных, определенная на множестве ![]() . Все точки области определения этой функции разделим на три группы:
. Все точки области определения этой функции разделим на три группы:
![]() , где
, где ![]() и
и ![]()
Эти точки являются внутренними точками множества ![]() .
.
![]() , где
, где ![]() и
и ![]()
В окрестности таких точек не существует точек, отличных от их самих, поэтому точки такого вида являются изолированными точками [1, c. 64].
![]() , где
, где ![]() и
и ![]()
Окрестность существует только для ![]() в смысле
в смысле ![]() .
.
![]() , где
, где ![]() и
и ![]()
Окрестность существует только для ![]() в смысле
в смысле ![]() .
.
Поэтому любая окрестность таких точек содержит бесконечно много точек из ![]() , то есть точки такого вида являются предельными точками [1, c. 64].
, то есть точки такого вида являются предельными точками [1, c. 64].
Класс функций, определенных в предельных точках, назовем классом предельных функций.
Функции, заданные в области ![]() , будут предельными
, будут предельными
![]()
![]()
![]()
![]()
![]() И функция, заданная в области
И функция, заданная в области ![]()
![]()
Непрерывность предельных функций на промежутке
Предельную функцию ![]() назовем непрерывной на промежутке
назовем непрерывной на промежутке ![]() или
или ![]() , если для всех точек
, если для всех точек ![]() или
или ![]() из этого промежутка существует повторный предел равный одной константе на всем промежутке
из этого промежутка существует повторный предел равный одной константе на всем промежутке
![]()
![]()
Предельный переход к ![]() и
и ![]() или
или ![]() осуществляется при фиксированном
осуществляется при фиксированном ![]() или
или ![]() .
.
Если же значение повторного предела не равно константе или равно константе не равной ![]() , в какой либо точке промежутка, то предельная функция в этой точке терпит разрыв.
, в какой либо точке промежутка, то предельная функция в этой точке терпит разрыв.
Повторный предел, очевидно, имеет вид
![]()
![]()
Где
![]()
![]()
Исследуем на непрерывность предельные функции, заданные в области
![]()
![]()
Т. к.
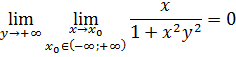
то, предельная функция непрерывна в заданном промежутке.
![]()
Т. к.
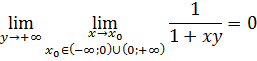
И
![]()
то предельная функция непрерывна на промежутке ![]() и терпит разрыв в точке
и терпит разрыв в точке ![]() .
.
![]()
Т. к.

то, предельная функция непрерывна в заданном промежутке.
![]()
Т. к.
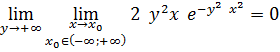
то, предельная функция непрерывна в заданном промежутке.
![]() И функцию, заданную в области
И функцию, заданную в области ![]()
![]()
Т. к.
![]()
И
![]()
![]()
то предельная функция непрерывна на интервале ![]() и терпит разрыв в точках
и терпит разрыв в точках ![]() .
.
Равномерность предельных функций на промежутке
Особенно интересен характер поведения предельной функции ![]() в точке
в точке ![]() , в которой существует конечный простой предел равный константе
, в которой существует конечный простой предел равный константе
![]()
Здесь возникает следующий вопрос: будет ли предельная функция ![]() равномерной в этой точке? То есть точка
равномерной в этой точке? То есть точка ![]() будет являться потенциальной точкой неравномерности предельной функции
будет являться потенциальной точкой неравномерности предельной функции ![]() .
.
Сформулируем определение равномерности для предельной функции для некоторого промежутка на «языке ![]() »:
»:
Определение 1. Если для любого числа ![]() существуют такие
существуют такие ![]() и
и ![]() , что для всех точек
, что для всех точек ![]() , координаты которых удовлетворяют неравенства
, координаты которых удовлетворяют неравенства
![]() и
и ![]()
где: ![]() , выполнятся неравенство
, выполнятся неравенство
![]()
то предельная функция ![]() равномерна по
равномерна по ![]() в замкнутом промежутке
в замкнутом промежутке ![]() .
.
Или что тоже
Определение 1*. Предельная функция ![]() равномерна по
равномерна по ![]() в замкнутом промежутке
в замкнутом промежутке ![]() , если для нее существует двойной предел при
, если для нее существует двойной предел при ![]() и
и ![]() , где
, где ![]() , равный одной константе всем промежутке
, равный одной константе всем промежутке
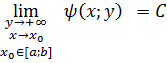
Равномерность предельной функции не гарантирует ее непрерывность, обратное же утверждение в общем (но не в частном) случае неверно. Имеет место менее сильное определение равномерной непрерывности предельной функции.
Теорема 1. Предельная функция ![]() равномерно непрерывна по
равномерно непрерывна по ![]() в замкнутом промежутке
в замкнутом промежутке ![]() , если существует простой предел по
, если существует простой предел по ![]() как функция одной переменной
как функция одной переменной ![]()
![]()
и повторный предел, равный одной константе на всем промежутке
![]()
По самому определению равномерности предельной функции приходим к следующему утверждению
Теорема 2. Если предельная функция ![]() равномерно непрерывна по
равномерно непрерывна по ![]() на некотором промежутке
на некотором промежутке ![]() , то есть
, то есть
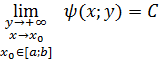
![]()
то допустим предельный переход
![]()
Поточечная равномерность предельных функций на промежутке
Для класса предельных функций понятие их равномерности на промежутке отлично от понятия равномерности в точке. К примеру, при определении равномерности предельной функции ![]() в точке
в точке ![]() , может случиться так, что двойной предел в этой точке будет равен константе и не будет равен двойному пределу на промежутке
, может случиться так, что двойной предел в этой точке будет равен константе и не будет равен двойному пределу на промежутке ![]() , то есть
, то есть
![]()
Хотя
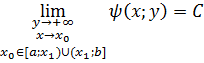
![]()
Поэтому если попытаться переформулировать определение 1 со случая равномерности предельной функции на промежутке для случая равномерности предельной функции в точке, то точка неравномерности функции будет принята за точку равномерности, что обязательно приведет к ошибке. Поэтому класс рассматриваемых функций должен быть сужен. Необходимо положить ![]() , тогда для повторного предела будем иметь
, тогда для повторного предела будем иметь
![]()
Сформулируем определение равномерности для предельной функции![]() в точке
в точке ![]() на «языке
на «языке ![]() »:
»:
Определение 2. Если для любого числа ![]() существуют такие
существуют такие ![]() и
и ![]() , что для всех точек
, что для всех точек ![]() , координаты которых удовлетворяют неравенствам
, координаты которых удовлетворяют неравенствам
![]() и
и ![]()
выполнятся неравенство
![]()
то предельная функция ![]() равномерна в точке
равномерна в точке ![]() .
.
Или что тоже
Определение 2*. Предельная функция ![]() равномерна в точке
равномерна в точке ![]() , если для нее существует двойной предел при
, если для нее существует двойной предел при ![]() и
и ![]() равный нулю
равный нулю
![]()
Требование равномерности предельной функции в любой точке промежутка сильнее требования равномерности предельной функции на промежутке.
Предельную функцию ![]() будем называть поточечно равномерной по
будем называть поточечно равномерной по ![]() на некотором промежутке
на некотором промежутке ![]() , если она равномерна в любой точке этого промежутка.
, если она равномерна в любой точке этого промежутка.
Сформулируем определение поточечной равномерности предельной функции на промежутке на «языке ![]() »:
»:
Определение 3. Если для любого числа ![]() существуют такие
существуют такие ![]() и
и ![]() , что для всех точек
, что для всех точек ![]() , координаты которых удовлетворяют неравенствам
, координаты которых удовлетворяют неравенствам
![]() и
и ![]()
где: ![]() , выполнятся неравенство
, выполнятся неравенство
![]()
то предельная функция ![]() поточечно равномерна по
поточечно равномерна по ![]() в замкнутом промежутке
в замкнутом промежутке ![]() .
.
Или, что тоже
Определение 3*. Предельная функция ![]() поточечно равномерна по
поточечно равномерна по ![]() в замкнутом промежутке
в замкнутом промежутке ![]() , если она равномерна в любой точке этого промежутка, то есть существует двойной предел при
, если она равномерна в любой точке этого промежутка, то есть существует двойной предел при ![]() и
и ![]() , где
, где ![]() , равный нулю
, равный нулю
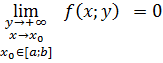
Исследуем на равномерность предельные функции, заданные в области
![]()
![]()
По теореме 1 получаем
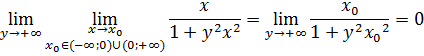
Полагая ![]() в
в

Получаем

А переходя к полярным координатам ![]() , будем иметь
, будем иметь
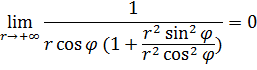
Отсюда следует, что предельная функция поточечно равномерна в заданном промежутке.
![]()
По теореме 1 получаем
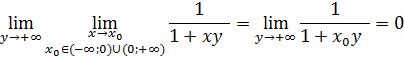
Полагая ![]() в
в

Получаем
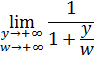
А переходя к полярным координатам ![]() , будем иметь
, будем иметь
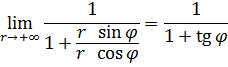
Отсюда следует, что предельная функция поточечно равномерна на промежутке ![]() и неравномерна в точке
и неравномерна в точке ![]() .
.
![]()
По теореме 1 получаем

Полагая ![]() в
в

Получаем
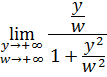
А переходя к полярным координатам ![]() , будем иметь
, будем иметь

Отсюда следует, что предельная функция поточечно равномерна на промежутке ![]() и неравномерна в точке
и неравномерна в точке ![]() .
.
![]()
По теореме 1 получаем
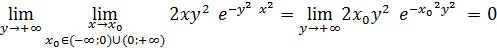
Полагая ![]() в
в
![]()
Получаем
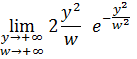
А переходя к полярным координатам ![]() , будем иметь
, будем иметь
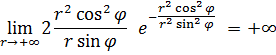
Отсюда следует, что предельная функция поточечно равномерна на промежутке ![]() и неравномерна в точке
и неравномерна в точке ![]() .
.
![]() И предельной функции, заданной в области
И предельной функции, заданной в области ![]()
![]()
По теореме 1 получаем
![]()
А для ![]() имеем
имеем
![]()
![]()
Отсюда следует, что предельная функция поточечно равномерна на интервале ![]() и неравномерна в точках
и неравномерна в точках ![]() .
.
Список литературы:
1.Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: ФИМАТЛИТ, 2012. — 572 с. — ISBN 978-5-9221-0266-7.
2.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учебник: в 3 т. Т. 1. — 9-е изд., стер. — СПб.: Лань, 2009. — 608 с.: ил. — (Учебники для вузов. Специальная книга).
дипломов


Оставить комментарий