АЛГОРИТМ  ТЕРМИНАЛЬНОГО  УПРАВЛЕНИЯ  СИСТЕМОЙ  ТРЕТЬЕГО  ПОРЯДКА  С  ТРЕМЯ  НУЛЕВЫМИ  ПОЛЮСАМИ  В  УСЛОВИЯХ  ОГРАНИЧЕННЫХ  ПОМЕХ

Кучеров  Дмитрий  Павлович

д-р  техн.  наук,  с.н.с.,  профессор,  НАУ,  г.  Киев,  Украина

E-mail:  d_kucherov@ukr.net

Козуб  Андрей  Николаевич

канд.  техн.  наук,  с.н.с.,  доцент,  НАУ,  г.  Киев,  Украина

E-mail: 

Введение.  Методам  и  алгоритмам  управления,  позволяющим  обеспечить  высокую  точность  управления  в  ограниченное  время,  в  последнее  время  в  научной  литературе  уделяется  значительное  внимание.  К  таким  методам  относятся  и  методы  терминального  управления,  позволяющие  реализовать  перевод  объекта  из  произвольной  точки  пространства  в  заданную  за  минимальное  время.

В  работах  по  теории  автоматического  управления  эта  задача  для  систем  с  полностью  известной  информацией  о  постоянных  параметрах  системы  формулируется,  как  задача  о  максимальном  быстродействии.  Строгое  доказательство  существования  закона  управления  и  формулировка  необходимых  и  достаточных  условий  существования  решения  задачи  представлено  в  работах  советского  ученого  Л.С.  Понтрягина  и  его  последователей  [1,  6].  Предлагаемый  этими  учеными  подход  предполагает  решение  во  временной  области.  Как  известно,  управляющее  воздействие  имеет  кусочно-непрерывный  (импульсный)  характер  и  знакопеременно.  Инженерный  подход  к  решению  задачи  максимального  быстродействия  основан  на  представлении  динамической  системы  в  фазовой  плоскости  и  характере  закона,  данный  подход  связывают  с  именем  А.А.  Фельдбаума  [8]. 

К  сожалению,  оптимистические  прогнозы  относительно  первых  удач  в  области  поиска  решений  для  известных  динамических  систем  столкнулись  с  рядом  непреодолимых  трудностей.  Прежде  всего,  такие  трудности  вызваны  возможностью  получения  удовлетворительных  решений  для  динамических  систем,  порядок  которых  выше  второго.  Классический  пример  динамической  системы  с  двумя  нулевыми  полюсами,  называемой  в  литературе  двойным  интегратором,  имеет  ограниченное  применение.  Реальные  системы  инерционны,  характеризуются  запаздываниями,  имеют  более  сложную  математическую  модель,  точные  параметры  которой  могут  быть  неизвестны,  фазовые  координаты  измеряются  с  помехами,  расчет  управляющего  воздействия  производится  с  различного  рода  вычислительными  ошибками,  в  результате  чего  система  может  совершать  малые  колебания  в  окрестности  области  цели.

Системы,  построенные  на  принципе  управления  в  фазовом  пространстве,  обладают  более  высокой  точностью  по  сравнению  с  теми,  которые  построены  во  временной  области,  что  характерно  для  замкнутых  систем.  Следствием  такого  подхода  являются  скользящие  режимы,  которые  в  общем  случае  являются  нежелательными  [7].  Современными  исследователями  предлагаются  различные  подходы  для  преодоления  возникающих  трудностей.  Так  в  [3],  эта  задача  решается  методами  обратных  задач  динамики,  приводя  исходную  сложную  модель  к  модели  второго  порядка  с  дальнейшим  упрощением,  сводя,  в  конечном  счете,  ее  к  модели  с  законом  управления  для  двойного  интегратора.  Очевидно,  что  это  может  быть  применимым  в  случаях,  когда  требований  к  высокой  точности  динамических  систем  не  предъявляется.  Более  перспективный  подход,  развиваемый  сравнительно  недавно  предлагается  в  работах  [9—12],  основывается  на  комбинированном  управлении,  при  котором  закон  управления  состоит  из  двух  частей,  каждая  из  которых  работает  в  своем  диапазоне  ошибок  измерения.  При  этом  импульсный  характер  управления  имеет  место  в  диапазоне  больших  ошибок,  а  в  диапазоне  незначительных  ошибок  использован  пропорциональный  закон  управления.  Это  позволяет  повысить  точность  работы  системы,  а  также  исключить  в  реализуемой  системе  значительных  временных  затрат  на  управление  и  малых  колебаний  в  окрестности  области  цели  [7,  8].

Однако,  для  систем  со  сложной  динамикой  модель  двойного  интегратора  не  является  пригодной,  ввиду  наличия  ошибок  в  системах  с  возможными  ускорениями.  В  задачах,  где  требуется  обеспечить  нулевую  ошибку  при  постоянном  ускорении  при  определении  закона  управления  целесообразно  использовать  модель  тройного  интегратора.  Описание  модели  тройного  интегратора  впервые,  по  нашим  данным,  было  представлено  в  работе  [13],  некоторые  вопросы  управления  изучались  [2,  5]. 

Закон  управления  тройным  интегратором  с  единичным  коэффициентом  усиления  был  представлен  А.А.  Фельдбаумом  в  работе  [8]  без  каких-либо  подтверждений,  а  с  произвольным  коэффициентом  усиления  в  работах  американских  ученых  [9,  12].  В  этих  работах  предполагается,  что  поверхность  переключения  имеет  вид  пласта  некоторой  толщины,  в  котором  закон  управления  становится  пропорционального  вида.  Некоторые  вопросы  управления  моделью  тройного  интегратора  представлены  в  [5].

В  статье  предполагается  обобщение  работ  [5,  8,  9,  12]  и  новые  результаты  решения  данной  задачи  для  случая,  когда  коэффициенты  тройного  интегратора  разные  в  отличие  от  [9,  12],  где  интегратор  имеет  только  один  коэффициент  усиления,  область  цели  имеет  вид  эллипса,  а  также  исследуются  вопросы  наиболее  существенного  влияния  помех  -  по  каналам  измерения  фазовых  координат  в  отличие  от  [12],  где  исследован  случай  наличия  возмущений  в  канале  управления. 

Постановка  задачи.  Пусть  имеется  динамическая  система,  которая  в  динамике  характеризуется  нулевой  ошибкой  при  постоянном  ускорении  [13].  Схематически  эта  система  представляется  цепью  трех  последовательно  соединенных  интеграторов  и  контролера,  управляющего  этой  цепью.  Предполагается,  что  контроллер  обеспечивает  отработку  динамическим  объектом  требуемой  траектории,  изменяющейся  по  линейному  закону,  т.  е. 

,                                 (1)

где:  a>0,  b,c³0  известные  параметры  входной  величины.  Предполагается  также,  что  начальное  состояние  динамической  системы  не  совпадает  с  заданной  траекторией  движения.  Система  управления  должна  обеспечить  выход  на  траекторию  и  нахождение  на  ней  в  пределах  времени  управления.  Для  этого  контроллер  должен  сформировать  закон  управления  u(t)  с  учетом  знания  выходной  величины  и  ее  производных,  а  также  производных  входной  величины  r(t).  Схема  такой  системы  может  быть  представлена  на  рис.  1.

Рисунок  1.  Структура  системы  с  тройным  интегратором  и  шумами  в  каналах  измерения

На  рис.1  введены  следующие  обозначения:  r  (t)  и    —  входной  и  выходной  сигналы  контроллера,  x  (t)  —  представляет  выходную  величину  системы,  а    и    —  являются  первой  и  второй  производными  выходной  величины.  Предполагается,  что  коэффициенты  передачи  интеграторов  k_i  не  одинаковы,  отличны  от  единицы,  известно,  что  они  могут  находиться  в  интервалах 

.                                (2)

Измерение  фазовых  координат  системы  x_i  производится  на  фоне  мешающих  шумов,  статистическая  природа  которых  либо  неизвестна,  либо  недостаточно  времени  на  их  изучение,  а  известны  только  уровни  N_i,  которыми  они  ограничены,  а  именно,

,                                  (3)

где:  n_i(t)  —  шумы  в  каналах  измерения,  |n_i(t)|£  N_imax.

Тогда  система,  представленная  на  рис.1,  может  быть  описана  такой  системой  уравнений

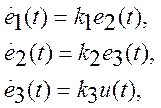                                   (4)

в  которой  e₁,  e₂,  e₃  —  отклонения  выходной  величины,  ее  первой  и  второй  производных  от  задания  соответственно,  т.  е. 

,  ,  ;  .(5)

Для  системы  (4)  считаются  заданными  начальное  состояние  e(t₀)=e₀  в  момент  времени  t₀=0,  определяемое  координатами  ,  и  конечное  е(t_к)=e_к  в  момент  t=t_к,  где  ,  а  W  —  область  достижимости.  Для  обеспечения  требования  минимальности  времени  выхода  t_min  динамической  системы  (4)  на  заданную  траекторию  (1),  т.  е.  Dt  =  (t_к–t₀)  =  min  и    будем  рассматривать  (4)  как  терминальную  динамическую  систему  с  минимальным  временем  перехода  в  конечное  состояние. 

В  статье  ставится  и  решается  задача  синтеза  закона  управления  динамической  системой  (4),  представляющей  последовательность  трех  интеграторов  с  коэффициентами  передачи  k_i,  заданными  соотношениями  (2),  по  информации  об  отклонениях  измерения  фазовых  координат  системы  (3),  (5)  в  условиях  ограниченных  помех.

Управление  с  полностью  известными  параметрами.  Для  обеспечения  минимальности  времени  управления  в  случае  известных  параметров  системы  задачу  управления  следует  рассматривать  как  оптимальную  по  быстродействию.  Закон  оптимального  управления  объектом  (4),  обеспечивающий  заданную  динамику  системы  без  помех,  выбирается  в  форме 

                    (6)

В  уравнении  (6)  приняты  обозначения 

,                      (7)

,                              (8)

,                     (9)

,                                          (10)

а  коэффициенты  с₁,  с₂,  с₃,  с₄ 

,  ,  ,  .(11)

Функция  f₁(e)  в  пространстве  eγ  представляет  гиперповерхность  (рис.  2),  разделяющую  пространство  управлений  u(e)  на  два  возможных  полупространства  u₊  и  u_-,  т.  е.  u(e)=u₊Èu_-.  Закон  управления  (6)  обеспечивает  движение  объекта  из  состояния  е₀  в  состояние  е_к=0.  В  данном  случае  конечная  цель  движения  объекта  —  начало  координат,  точка  с  координатами  (0,  0,  0).

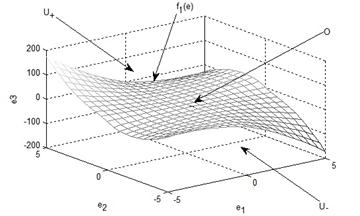
Рисунок  2.  Вид  функции  f₁(e)  в  фазовом  пространстве  е₁,  е₂,  е₃

Движение  фазовой  точки  происходит  по  некоторой  кусочно-гладкой  траектории,  которая  ведет  объект  из  произвольной  начальной  точки  заданного  фазового  пространства  в  начало  координат.  Минимальность  во  времени  достигается  чередованием  знака  управляющего  воздействия  в  моменты  пересечения  гиперповерхности  f₁(e)  и  f₃.  Максимальное  число  интервалов  управления  для  решения  поставленной  задачи  не  превосходит  трех,  что  полностью  согласуется  с  теоремой  об  n-интервалах  А.А.  Фельдбаума.  Уравнения  (6)—(9)  совпадают  с  уравнениями  (33)—(35)  из  [9]  в  случае,  если  принять  коэффициенты  k₁=k₂=1,  а  k₃=K,  как  и  должно  быть.

Управление  в  условиях  помех.  Анализ  численного  решения  задачи  с  использованием  ПЭВМ  приводит  к  необходимости  учета  ошибок  квантования  и  округления,  которые  имеют  место  при  расчетах  на  вычислительных  машинах  с  конечной  разрядной  сеткой,  действие  которых  сводится  к  появлению  бесконечных  циклов  в  окрестности  начала  координат.  Исключение  их  влияния  приводит  к  необходимости  введения  в  окрестности  начала  координат  некоторой  области  W_ц,  где  действие  управления  прекращается,  имеет  смысл  назвать  областью  достижимости.  В  [9]  предлагается  введение  области  W_ц  в  виде  пласта,  получаемого  смещением  поверхности  f₁(e)  по  координате  e₁  на  величину  e  относительно  начала  координат  как  в  положительную,  так  и  отрицательную  стороны,  а  в  [12]  область  W  предлагается  представить  в  виде  эллипса 

,                                      (12)

где:  P  —  положительно-определенная  матрица, 

k>0  —  число,  графический  вид  которого  представлен  на  рис.  3.

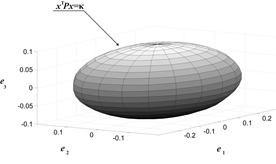
Рисунок  3.  Эллипсоидальная  область  в  алгоритме  управления

Будем  предполагать,  что  динамика  динамической  системы  с  рассматриваемой  областью  достижимости  характеризуется  приемлемой  точностью,  для  которой  ошибка  системы  не  превышает  вычислительную  точность  системы.  Условием  успешного  решения  задачи  является  необходимость  фиксации  фазовых  координат  в  эллипсе.  Алгоритм  фиксации  заключается  в  контроле  всех  фазовых  координат  в  эллипсе,  т.  е.  если  ,  где  W_ц  —  область  достижимости,  а  значит,  цель  управления  достигнута. 

В  случае,  когда  движение  динамической  системы  происходит  в  условиях  воздействия  помех,  динамика  объекта  управления  может  существенно  изменяться  так,  что  будут  происходить  ложные  смены  знака  управляющего  воздействия  контроллером,  зацикливание  системы  управления,  что  приводит  к  преждевременному  износу  исполнительной  части  системы.  Исследования  показали,  наибольшее  воздействие  на  динамику  объекта  оказывают  помехи  n_i,  где  i=1….3  номер  канала,  возникающие  в  каналах  измерения  фазовых  координат. 

Наибольший  интерес  у  исследователей  [4]  вызывают  помехи,  статистическая  природа  которых  априори  неизвестна,  что  имеет  место  в  случаях,  когда  у  исследователя  недостаточно  времени  для  изучения  ее  статистических  свойств  или  же  это  помеха  «играющего»  типа  [4].  К  известной  информации  следует  относить  только  уровень  N,  которым  эта  помеха  ограничена.  Блокировать  действие  помехи  возможно  только  лишь  в  том  случае,  когда  фазовые  координаты  объекта  гарантированно  находятся  в  области  определенного  знака  сигнала  управления.  Это  достигается  целенаправленным  сдвигом  измеренных  координат  фазовой  точки  в  глубину  области  действующего  в  данный  момент  знака  (в  сторону  от  f₁(e))  на  величину  уровня  помехи  N.  При  этом  сама  фазовая  точка  динамического  объекта  сдвигается  на  величину    относительно  своего  текущего  положения.  Переключение  в  этом  случае  происходит  при  гарантированном  нахождении  фазовых  координат  объекта  в  области  действия  другого  знака  управления.  С  учетом  этого  замечания  закон  управления  может  быть  переписан  в  виде,  в  котором  значения  е(t)  фазовых  координат  в  (6)  заменяются  на  их  сдвинутые  величины 

.                            (13)

Сдвиги  фазовых  координат  (12)  приведут  в  свою  очередь  к  расширению  области  W,  форма  области  достижимости  та  же

                           (14)

где:  k¢>k.

Модифицированный  закон  управления.  При  одновременном  удовлетворении  показателей  системы  управления  как  по  времени  управления,  так  и  по  точности  целесообразность  в  терминальном  управлении  возникает  только  лишь  при  больших  отклонениях,  когда  начальное  значение  фазовой  траектории  находится  вне  области  W  для  приведения  фазовой  точки  в  эту  область  и  обеспечения  попадания  в  область  достижимости  W.  Далее  задача  решается,  используя  иной  закон  управления,  например,  пропорциональный,  т.  е. 

,                                    (15)

где:  A  —  вектор  коэффициентов.

Если  же  представить  закон  управления  (6)  в  области  значительных  ошибок  как  u_тер,  а  в  области  малых  (15)  как  u_пр(е),  тогда  модифицированный  закон  управления  запишется  в  виде

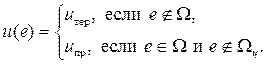                        (16)

В  (16)  W  —  область  переключения  (14)  и  W_ц  —  область  достижимости.  Отличительной  особенностью  функционирования  алгоритма  (16)  является  наличие  алгоритма  фиксации  попадания  объекта  в  области  достижимости  (рис.  4).  В  отличие  от  предыдущего  случая,  при  котором  возникала  необходимость  только  контроля  наличия  координат,  в  условиях  помех  ситуация  может  быть  еще  хуже,  когда  измеренные  координаты  фазовой  точки  фиксируются  внутри  области  достижимости  W_ц,  а  реальные  координаты  объекта  находятся  вне  ее.  В  этом  случае  будет  являться  необходимым  фиксация  участка  траектории  по  нескольким  измерениям,  т.е.  так

.                (17)

Число  таких  измерений  зависит  от  длины  пути  соизмеримого  с  уровнем  помехи,  искажающем  соответствующие  координаты. 

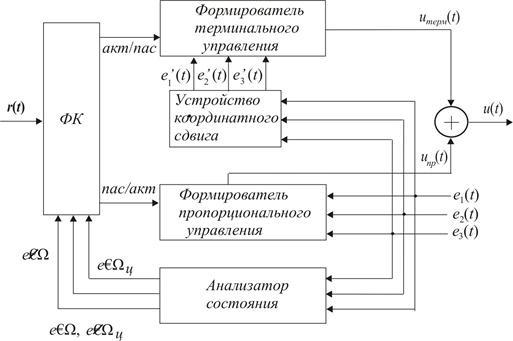
Рисунок  4.  Структура  контроллера  с  модифицированным  законом  управления

На  рис.4  представлена  структура  контроллера  с  модифицированным  законом  управления  (15),  основными  элементами  которой  являются  формирователь  команд  (ФК),  формирователь  терминального  управления,  формирователь  пропорционального  управлении,  устройство  координатного  сдвига,  анализатор  состояния  и  сумматор  сигналов  управления.  Контроллер  при  поступлении  задания  r(t)  выдает  команды  на  перевод  соответствующего  формирователя  в  активное  состояние,  выбор  активного  состояния  определяется  анализатором  по  значениям  координат  вектора  ошибок  относительно  области  цели.  После  фиксации  вектора  е(t)  в  области  цели  W_ц  по  правилу  (17)  оба  формирователя  отключаются. 

Моделирование.  Для  оценки  эффективности  закона  управления  (15)  проводилось  моделирование  динамики  объекта  управления  (4)  для  задающего  воздействия  (1)  в  различных  начальных  условиях  вектора  e₀.  Параметры  k_i  объекта  выбирались  из  интервала  0,1£k_i£10  таким  образом,  чтобы  общий  коэффициент  передачи  K=k₁k₂k₃  был  бы  отличен  от  1.  В  демонстрационном  примере  параметры  объекта  управления  принимались  равными

.

Отработке  подвергалось  задающее  воздействие  с  параметрами  a=0,1,  b=0,5,  с=1.  Измерение  фазовых  координат  происходит  с  шумами,  уровень  ограничения  которых  в  каждом  канале  |N_i|  £0,5.  Результаты  моделирования  выходных  координат  динамической  системы  (2)  представлены  на  рис.  5.

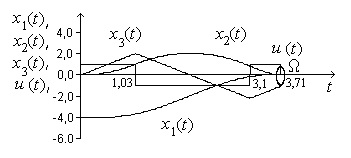
Рисунок  5.  Фазовые  траектории  динамической  системы  (2)  при  комбинированном  управлении

Сравнение  результатов  моделирования  для  ряда  испытаний  позволяет  сделать  вывод  о  достоверности  полученных  результатов. 

Выводы.  В  статье  предложено  решение  задачи  синтеза  закона  управления  динамической  системой,  движение  которой  происходит  с  постоянным  ускорением  и  при  наличии  ограниченных  по  уровню  помех,  действующих  на  систему  по  каналам  измерения.  Модель  динамической  системы  может  быть  представлена  последовательностью  трех  интеграторов  с  контроллером,  формирующим  закон  управления  в  виде  (6).  В  работе  показано,  что  одновременного  достижения  высоких  показателей  точности  и  времени  отработки  задания  возможно  при  модификации  закона  управления,  включающей  замечание  (12)  и  комбинацию  (16),  (17).  Результаты  моделирования  подтверждают  правильность  выдвинутых  утверждений.  Дальнейшие  результаты  исследований  предполагается  направить  на  изучение  свойств  динамической  системы  и  определения  закона  управления  в  условиях,  когда  уровень  ограничения  помехи  N  априори  неизвестен.

Список  литературы:

1.Болтянский  В.Г.  Математические  методы  оптимального  управления.  —  М.:  Наука,  1969.  —  408  с.

2.Козлов  А.И.  Полный  анализ  задачи  тройного  интегратора  /  А.И.  Козлов,  Д.Ю.  Муромцев  //  Автоматика  и  телемеханика.  —  2005.  —  №  1.  —  С.  3—12.

3.Крутько  П.Д.  Алгоритмы  терминального  управления  линейными  динамическими  системами  /  П.Д.  Крутько  //  Известия  РАН.  Теория  и  системы  управления.  —  1998.  —  №  6.  —  С.  33—45.

4.Кунцевич  В.М.  Управление  в  условиях  неопределенности:  гарантированные  результаты  в  задачах  управления  и  идентификации  /  Кунцевич  В.М.  —  К.:  Наук.  думка,  2006.  —  264  с.

5.Кучеров  Д.П.  Алгоритм  адаптивного  терминального  управления  тройным  интегратором  /  А.В.  Василенко,  Б.П.  Иванов,  Д.П.  Кучеров  //  Вісник  Вінницького  політехнічного  інституту.  —  2009.  —  №  2.  —  С.  22—27.

6.Понтрягин  Л.С.,  Болтянский  В.Г.,  Гамкрелидзе  Р.В.,  Мищенко  Е.Ф.  Математическая  теория  оптимальных  процессов.  4-е  изд.  —  М.:  Наука,  1983.  —  392  с.

7.Справочник  по  теории  автоматического  управления  /  [под  ред.  А.А.  Красовского].  —  М.:  Наука,  1987.  —  712  с.

8.Фельдбаум  А.А.,  Бутковский  А.Г.  Методы  теории  автоматического  управления.  —  М.:  Наука,  1971.  —  743  с.

9.Kaylon  M.  Design  of  continuous  time  controllers  having  almost  minimum  time  response  //  Transactions  of  the  ASME.  —  2002.  Vol.  124.  June.  —  P.  252—260.

10.Kucherov  D.P.  Synthesis  of  adaptive  controller  for  fixed-time  control  of  a  spinning  body  under  the  presence  of  bounded  noise  /  D.P.  Kucherov  //  Journal  of  automation  and  information  science.  —  2005.  Vol.  37.  Issue  1.  —  P.  29—38.  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  www.dl.begellhouse.com/journals/2b6239406278e43e,5aa280c9630a07e4.html  (дата  обращения:  28.04.13).

11.Kucherov  D.P.  The  synthesis  of  adaptive  terminal  control  algorithm  for  inertial  secondary  order  system  with  bounded  noises  /  D.P.  Kucherov  //  Journal  of  automation  and  information  science.  —  2007.  Vol.  39.  Issue  9.  —  P.  16—25.  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  http://www.dl.begellhouse.com/journals/2b6239406278e43e,04284c744990a95a.html  (дата  обращения:  28.04.13).

12.Pao  L.Y.  Proximate  time-optimal  control  of  third-order  servomechanisms  /  Pao  L.Y.,  Franklin  G.F.  //  IEEE  Transactions  on  Automatic  Control.  —  1993.  Vol.  38.  №  4.  —  P.  560—580.

13.Smith  О.J.М.  Feedback  control  systems.  —  New  York:  McGrowHill,  1958.  —  694  p.