РАЗЛОЖЕНИЕ  ДВОЙНЫХ  И  ТРОЙНЫХ  ИНТЕГРАЛОВ  ПО  БЕСКОНЕЧНЫМ  ДИАГОНАЛЯМ

Корнеев  Антон  Александрович

студент  3  курса,  факультет  точных  наук  и  инновационных  технологий  МГГУ  им.  Шолохова,  г.  Москва

E-mail:  predsedatel_2012@mail.ru

Дорошкевич  Ольга  Александровна

научный  руководитель,  канд.  физ.-мат.  наук,  доцент  МГГУ  им.  Шолохова,  г.  Москва

Вывод  разложения  двойных  интегралов  по  бесконечным  диагоналям

В  контексте  разложения  двойных  и  тройных  рядов  по  бесконечным  диагоналям  [1,  с.  61],  возникает  задача,  которая  заключается  в  обобщении  данной  теории  на  случай  несобственных  интегралов.

Пусть  в  бесконечной  прямоугольной  области    =[]  задана  некоторая  интегрируемая  (в  Римановом  смысле)  функция  двух  переменных  ,  для  которой  существует  конечный  двойной  несобственный  интеграл

Предполагается,  что  переменные    и  стремятся  к  бесконечности  по  множеству  действительных  чисел,  начиная  с    и    независимо  друг  от  друга.

Матрица  значений,  которые  принимают  переменные,  выглядит  следующим  образом  (здесь  мы  полагаем,  что  ):

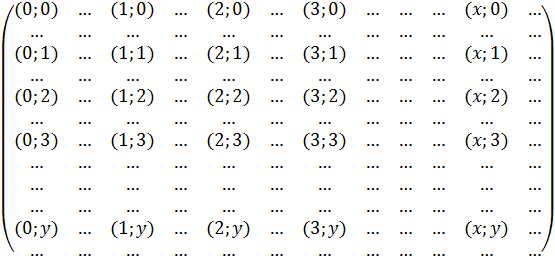
Её  следует  понимать  в  смысле  .

По  главной  бесконечной  диагонали  имеем

Над  главной  бесконечной  диагональю  имеем  бесконечные  диагонали

и  т.  д.

Подобным  же  образом  определяются  бесконечные  диагонали,  лежащие  под  главной  бесконечной  диагональю

и  т.  д.

Если  каждую  бесконечную  диагональ  матрицы  записать  построчно,  то  матрица  примет  следующий  вид

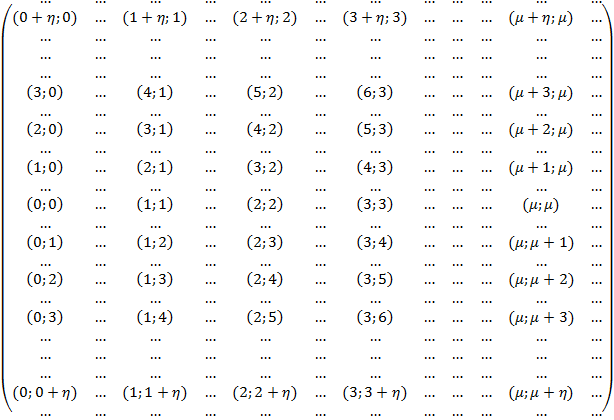
Поэтому,  область  интегрирования,  которая  представляет  собой  бесконечный  прямоугольник  в  двойном  несобственном  интеграле,  может  быть  разбита  на  две  области,  представляющие  собой  бесконечные  прямоугольники.  Здесь  для    получаем  формулу  разложения  двойных  интегралов  по  бесконечным  диагоналям 

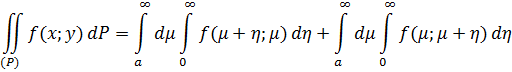
Заменяя    на    и    на  ,  для    и    получаем

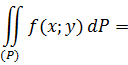
Свойства  разложения

Если  функция  симметрична  и  ,  то

Если  функция  кососимметрична  и  ,  то

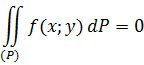
Рассмотрим  примеры,  где  путем  приведения  к  одной  бесконечной  прямоугольной  области  интегрирования,  повторные  интегралы  сводятся  к  более  простым

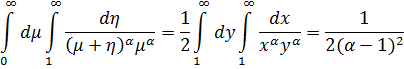
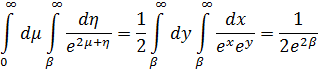
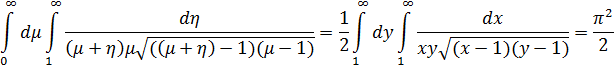
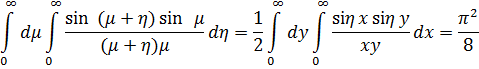
Вывод  разложения  тройных  интегралов  по  бесконечным  диагоналям  для  трех  переменных

Рассмотрим  сходящийся  тройной  интеграл,  заданный  в  области 

Для  ;  ;    составим  матрицу,  где  каждая  строчка  есть  главная  бесконечная  диагональ  матриц

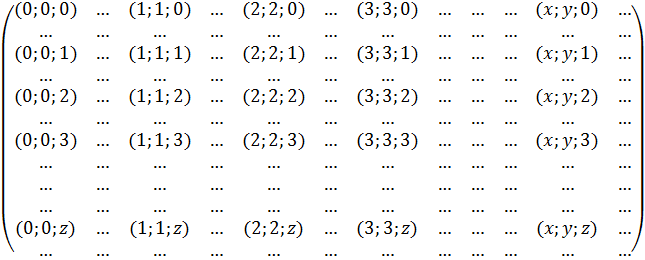
Если  каждую  бесконечную  диагональ  матрицы  записать  построчно,  то  матрица  примет  следующий  вид

Отсюда  получаем  сумму  повторных  интегралов  для  главных  бесконечных  диагоналей

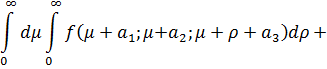
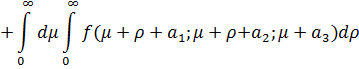
Таким  образом,  тройной  повторный  интеграл  приводится  к  двум  двойным  повторным  интегралам.  Проинтегрировав  их  как  двойные  повторные  интегралы  по  бесконечным  диагоналям,  приходим  к  формуле  разложения  тройных  интегралов  по  бесконечным  диагоналям  для  трех  переменных

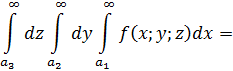
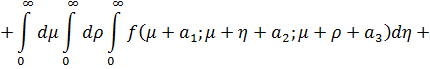
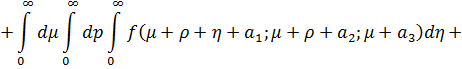
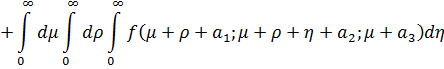
Список  литературы:

1.Корнеев  А.А.  Разложение  S-кратных  рядов  по  бесконечным  диагоналям  для  двух  и  трех  индексов  //  Теория  и  практика  современной  науки:  мат-лы  V  Междунар.  науч.-практ.  конф.:  в  2  т.  Т.  1.  —  М.:  Спецкнига,  2012.