ОБОБЩЕНИЕ  ТЕОРИИ  ДВОЙНЫХ  РЯДОВ  ПРИНГСГЕЙМА

Корнеев  Антон  Александрович

студент  3  курса,  факультет  точных  наук  и  инновационных  технологий  МГГУ  им.  Шолохова,  г.  Москва

E-mail:  predsedatel_2012@mail.ru

Дорошкевич  Ольга  Александровна

канд.  физ.-мат.  наук,  доцент  МГГУ  им.  Шолохова,  г.  Москва

 

Условие  сходимости  разложения  двойных  рядов  по  бесконечным  диагоналям

В  контексте  разложения  двойных  рядов  по  бесконечным  диагоналям  [1,  с.  61]  возникает  следующий  вопрос,  который  заключается  в  допустимости  представления  в  форме  данного  разложения  произведения  неабсолютно  сходящегося  и  абсолютно  сходящегося  ряда  и  двух  неабсолютно  сходящихся  рядов. 

Пустьисходящиеся  числовые  ряды.  Для  удобства  введем  следующие  обозначения

 

 

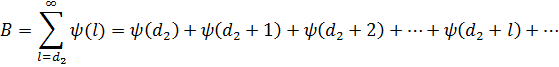
где:    и  .

Вплоть  до  Теоремы  2  положим  .

Теорема  1.  Произведение  двух  сходящихся  рядов    и  ,  взятое  по  бесконечным  диагоналям,  сходится,  если  сходится  ряд  по  главной  бесконечной  диагонали.

 

 

Доказательство.

Представим  формулу  произведения  двух  рядов  по  бесконечным  диагоналям  в  виде

 

 

Рассмотрим  первый  повторный  ряд.  По  условию  предполагается  сходимость  по  индексу  ,  поэтому  сходится  сумма  рядов

 

 

Имеем  неравенство

 

 

Для  другого  повторного  ряда  получаем

 

 

Ряды  в  неравенствах  сходятся  как  остатки  рядов    и  .  А  значит,  все  ряды  по  индексу    сходятся.

В  силу  того,  что  абсолютные  значения  рядов  по  бесконечным  диагоналям  оцениваются  абсолютным  значением  ряда  по  главной  бесконечной  диагонали

 

 

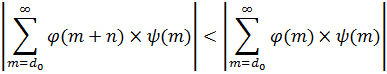
то  сходимость  разложения  сводится  к  сходимости  ряда  по  главной  бесконечной  диагонали  ч.  т.  д.

Возможны  три  случая,  когда  произведения  двух  рядов    и    по  бесконечным  диагоналям  могут  сходиться:

1.Ряды    и    сходятся  абсолютно

Если  ряды    и    сходятся  абсолютно,  то  разложение  по  бесконечным  диагоналям  имеет  место.

Сходимость  в  данном  в  случае  очевидна,  ибо  следует  из  абсолютной  сходимости  двойного  ряда.

2.Ряд    сходится  абсолютно,  а  ряд    относительно  (или    —  относительно,  а    —  абсолютно).

Для  определенности  положим,  что  ряд    сходится  абсолютно,  а  ряд    —  относительно.

Т.  к.  для  сходимости  повторных  рядов,  достаточна  сходимость  по  индексу  ,  то  для  первого  и  второго  повторного  ряда  достаточна  сходимость  рядов  представленных  суммой

 

 

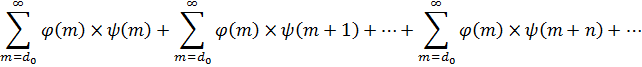
Эти  ряды  сходится  по  теореме  сравнения  рядов  [3,  с.  264],  причем  абсолютно

 

 

т.  к.

 

 

то  в  силу  неравенства

 

 

Получаем  утверждение  схожее  с  теоремой  Мертенса  [3,  с.  328]  для  сходимости  произведения  двух  рядов  в  форме  Коши:

Если  рядыи    сходятся,  причем  хоть  один  из  них  сходится  абсолютно,  то  разложение  по  бесконечным  диагоналям  имеет  место.

3.  Рядыи    сходятся  неабсолютно

Представим  неабсолютно  сходящиеся  ряды  в  следующем  виде

 

 

где  частичные  суммы  рядов

 

 

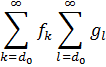
В  совокупности  ограничены:

 

  и 

 

А  числа    и    образуют  монотонную  последовательность,  стремящуюся  к  нулю:

 

 

То  есть  рядыи    сходятся  по  признаку  Дирихле  [3,  с.  307].  Здесь  мы  берем  признак  Дирихле  как  наиболее  общий  для  сходимости  неабсолютно  сходящихся  рядов,  исходя  из  того,  что  признак  Лейбница  [3,  с.  302]  и  признак  Абеля  [3,  с.  307]  являются  его  частными  случаями.

Рядсходится  только  в  двух  случаях:

1. 

То  есть  рядсходится  по  признаку  Дирихле,  причем,  если  сходится  ряд

 

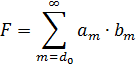
то  ряд    сходится  абсолютно,  в  противном  случае  условно

2. 

То  есть  рядсходится  только  тогда,  когда  сходится  ряд  .

Обобщение  теории  умножения  рядов

В  контексте  сходимости  повторных  рядов  возникает  вопрос:  будет  ли  их  сумма  равна  произведению  сумм?  На  это  вопрос  отвечает  следующая  теорема,  которую  мы  обобщили  и  для  произведения  по  квадратам.

Для  следующей  теоремы  положим 

Теорема  2.  Если  произведение  двух  сходящихся  рядов    и  ,  взятое  по  бесконечным  диагоналям  или  по  квадратам,  сходится,  то  его  сумма    равна  .

Доказательство.

Обозначим  бесконечные  диагонали  следующим  образом

 

 

 

и  их  частичную  сумму

 

 

легко  видеть  что

 

 

Разделим  это  равенство  почленнона  и  перейдем  к  пределу  при  .  Так  как  ,  то  по  теореме  Коши  [2,  с.  63]

 

 

С  другой  стороны

 

 

Отсюда  ,  ч.  и  тр.  д.  дляпроизведения  по  бесконечным  диагоналям.

Обозначим  квадраты  следующим  образом

 

 

 

И  их  частичную  сумму

 

 

легко  видеть  что

 

 

Разделим  это  равенство  почленно  на    и  перейдем  к  пределу  при  .  Так  как  ,  то  по  теореме  Коши

 

 

С  другой  стороны

 

 

Отсюда  ,  ч.  и  тр.  д.  дляпроизведения  по  квадратам.

Здесь  получаем  обобщение  теоремы  2  и  теоремы  Абеля  [3,  с.  329].

Теорема  2*.Еслипроизведение  двух  сходящихся  рядов    и  ,  взятое  по  бесконечным  диагоналям,  или  по  диагоналям  (в  форме  Коши),  или  по  квадратам,  сходится,  то  его  сумма    равна  .

Следствие  1.  Если  сходится  произведение  двух  рядов    и    по  бесконечным  диагоналям,  то  по  диагоналям  (в  форме  Коши)  и  по  квадратам  оно  сходится,  причем  к  той  же  сумме.

Для  произведения  по  бесконечным  диагоналям  это  следует  из  равенства  пределов

 

 

Для  произведения  по  квадратам  имеем

 

 

Отсюда  также  следует  что

 

 

Следствие  2.  Произведение  двух  сходящихся  рядов    и  ,  взятое  по  бесконечным  диагоналям,  по  диагоналям  (в  форме  Коши)  и  по  квадратам  сходится,  если  сходится  ряд  .

Остался  еще  один  способ  просуммировать  произведение  двух  сходящихся  рядов  —  это  представить  их  произведение  в  форме  повторного  ряда.

Теорема  3.  Произведение  двух  сходящихся  рядов    и    представленное  в  форме  повторных  рядов,  сходится  всегда,независимо  от  порядка  суммирования,  причем  к  произведению  сумм.

 

 

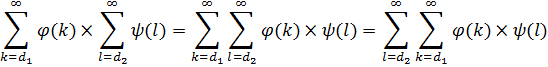
Доказательство. 

 

 

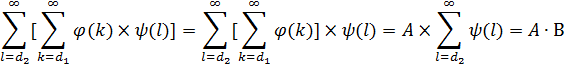
И  аналогично  для  другого  повторного  ряда

 

 

ч.  и  т.  д.

Если  двойной  ряд  можно  представить  в  виде  произведения  рядов

 

 

то  будем  говорить,  что  двойной  ряд  разделим  по  индексам    и  .

Вычисление  сумм  двойных  рядов  с  помощью  разложения  двойных  рядов  по  бесконечным  диагоналям

Пусть  дан  сходящийся  ряд,  где 

 

 

И  при  умножении  его  на  себя  выполняется  условие,  при  котором  произведение,  взятое  по  бесконечным  диагоналям,  сходится.  Общий  член  двойного  ряда,  полученный  данным  способом,  очевидно,  всегда  симметричен,  тогда  можно  записать  разложение  так

 

 

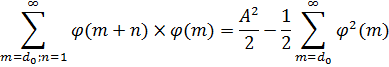
В  качестве  примеров  рассмотрим  следующие  двойные  ряды

 

 

Список  литературы:

1.Корнеев  А.А.  Разложение  S-кратных  рядов  по  бесконечным  диагоналям  для  двух  и  трех  индексов  //  Теория  и  практика  современной  науки:  мат-лы  V  Междунар.  науч.-практ.  конф.:  в  2  т.  Т.  1.  —  М.:  Спецкнига,  2012.

2.Фихтенгольц  Г.М.  Курс  дифференциального  и  интегрального  исчисления:  учебник:  в  3  т.  Т.  1.  —  9-е  изд.,  стер.  —  СПб.:  Лань,  2009.  —  608  с.:  ил.  —  (Учебники  для  вузов.  Специальная  книга).

3.Фихтенгольц  Г.М.  Курс  дифференциального  и  интегрального  исчисления:  учебник:  в  3  т.  Т.  2.  —  9-е  изд.,  стер.  —  СПб.:  Лань,  2009.  —  800  с.:  ил.  —  (Учебники  для  вузов.  Специальная  книга).