АНАЛОГ  ЗАДАЧИ  ДИРИХЛЕ  ДЛЯ  УРАВНЕНИЯ  В  ЧАСТНЫХ  ПРОИЗВОДНЫХ  ВТОРОГО  ПОРЯДКА  С  ОТКЛОНЯЮЩИМСЯ  АРГУМЕНТОМ

Бжеумихова  Оксана  Игоревна

аспирант  кафедры  дифференциальных  уравнений  Кабардино-Балкарского  государственного  университета,  г.  Нальчик

E-mail: 

ANALOG  THE  DIRICHLET  PROBLEM  FOR  THE  PARTIAL  DIFFERENTIAL  EQUATION  OF  SECOND  ORDER  WITH  DEVIATING  ARGUMENTS

Bzheumihova  Oksana  Igorevna

postgraduate  student  of  differential  equations  department  of  Kabardino-Balkarian  State  University,  Nalchik

АННОТАЦИЯ

Исследован  аналог  задачи  Дирихле  для  уравнения  в  частных  производных  второго  порядка  с  отклоняющимся  аргументом  в  прямоугольной  области.  Вопрос  разрешимости  задачи,  в  требуемом  классе  функций,  редуцирован  к  разрешимости,  соответствующего  обыкновенного  дифференциального  уравнения  с  отклоняющимся  аргументом,  решение  которого  построено  с  помощью  функции  Грина.

ABSTRACT

Investigates  analogue  of  the  Dirichlet  problem  for  partial  differential  equations  of  the  second  order  with  deviating  argument  in  a  rectangular  area.  Question  solvability  in  the  required  class  of  functions  is  reduced  to  the  solvability  of  the  corresponding  ordinary  differential  equations  with  deviating  argument,  the  solution  of  what  has  been  built  with  the  help  of  the  Green's  function.

Ключевые  слова:  уравнение  в  частных  производных;  задача  Дирихле;  преобразование  Фурье;  функция  Грина;  отклоняющийся  аргумент.

Keywords:  partial  differential  equation;  the  Dirichlet  problem;  the  Fourier  transform;  the  Green's  function;  deviating  argument.

Продолжая  исследования  уравнений  с  отклоняющимся  аргументом  и  краевых  задач  для  них  [6],  [7],  [2]—[4],  рассмотрим  уравнение

в  области  ,  где    —  суммируемая,    —  измеримая  функции,  ,  .

Задача  D.  Найти  регулярное  в  области    решение    уравнения  (1)  из  класса  ,  удовлетворяющее  краевым  условиям

где:    —  заданные  достаточно  гладкие  функции,  причем  ,  ,  ,  .

Применяя  конечное  синус-преобразование  Фурье  [7]

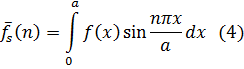
и  учитывая  условия  (2),  аналогично  [2],  получим:

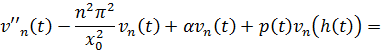
где 

.

В  частном  случае,  при    уравнение  (5)  принимает  вид:

Применяя  преобразование  (4)  к  условиям  (3),  будем  иметь

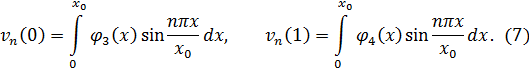
Далее,  вводя  замену

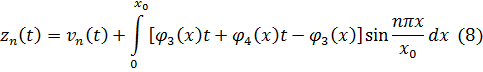
приведем  задачу  (6),  (7)  к  соответствующей  однородной  задаче:

где

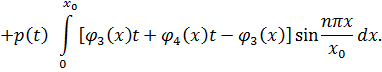
Используя  результаты  работы  [1]  представим  решение  полученной  задачи  (9),  (10)  в  виде:

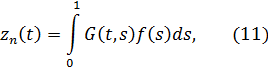
где:    —  функция  Грина  уравнения  (9).

Из  (8)  с  учетом  (11)  находим:

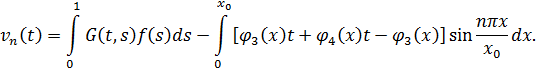
Применяя  к  последнему  неравенству,  обратное  синус-преобразование  Фурье  [5]

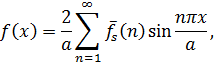
получим:

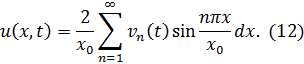
Следовательно,  решение  задачи  D,  при  указанных  предположениях  относительно  ,  представимо  в  виде  (12).

Так  как  система    образует  базис  в  ,  то  ряд  (12)  сходится  в    при  любом  .

Следуя  [6],  [4]  предположим,  что  ,  ,  т.е.  что  задача  D  однородна.  Тогда  на  оснований  равенств  (8),  (9),  будем  иметь    для  всех    и  .  Таким  образом  убеждаемся  в  единственности  решения  задачи  D.

Список  литературы:

1.Иноземцева  И.Н.,  Комленко  Ю.В.,  Пак  С.А.  Построение  функции  Грина  для  дифференциального  уравнения  с  отклоняющимся  аргументом  //  Математические  заметки.  —  1975.  —  Т.  17,  —  №  3.  —  С.  443—448.

2.Лесев  В.Н.,  Бжеумихова  О.И.  Задачи  для  смешанных  уравнений  и  уравнений  с  отклоняющимся  аргументом.  Единственность  и  существование  решений.  Saarbrucken  (Germany):  Palmarium  Academic  Publishing.  2012.  —  147  р.

3.Лесев  В.Н.,  Бжеумихова  О.И.  Об  однозначной  разрешимости  задачи  Неймана  для  эллиптического  уравнения  с  отклоняющимся  аргументом  //  Экологический  вестник  научных  центров  ЧЭС,  —  2012.  —  №  3.  —  С.  41—46.

4.Лесев  В.Н.,  Бжеумихова  О.И.  Применение  метода  Фурье  к  исследованию  задачи  Дирихле  для  уравнения  с  отклоняющимся  аргументом  и  оператором  Лапласа  в  главной  части  //  Политематический  сетевой  электронный  научный  журнал  Кубанского  государственного  аграрного  университета.  —  2012.  —  №  07(81).  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ej.kubagro.ru/2012/07/pdf/46.pdf

5.Снеддон  И.  Преобразования  Фурье.  М.:  Иностранная  литература,  1955.  —  667  с.

6.Bzheumikhova  O.I.,  Lesev  V.N.  Application  of  Fourier  method  to  investigation  of  the  Dirichlet  problem  for  partial  differential  equations  with  deviating  arguments  //  International  Journal  of  Differential  Equations  and  Applications.  —  2013.  —  Vol.  12,  —  №  2.  —  P.  103—120.

7.Bzheumikhova  O.I.,  Lesev  V.N.  On  the  issue  of  the  relationships  of  differential  equations  with  distributed  deviating  arguments  and  equations  with  fractional  integrals  //  Modern  scientific  research  and  their  practical  application.  —  2012.  —  Vol.  J31209.  —  P.  16—19.