ПРИБЛИЖЕННОЕ  РЕШЕНИЕ  ЗАДАЧИ  О  ТЕЧЕНИИ  ГАЗА  НАД  СЖИМАЕМОЙ  ЖИДКОСТЬЮ

Ерунова  Ирина  Борисовна

канд.  физ.-мат.  наук,  доцент,  Национальный  минерально-сырьевой  университет  «Горный»,  г.  Санкт-Петербург

E-mail:  irina.erunova@mail.ru

В  работе  рассматривается  процесс  движения  вязкого  газа  над  сжимаемой  жидкостью  как  задачи  с  движущейся  свободной  границей  раздела  сред,  на  которой  происходит  переход  из  сжимаемой  жидкости  в  вязкий  газ.  Существование  единственного  точного  решения  задачи  об  испарении  несжимаемой  жидкости  было  доказано  в  [1,  с.  26].  В  [2,  с.  95]  были  получены  оценки  скорости  сходимости  приближенного  решения  нестационарной  задачи  о  движении  несжимаемой  жидкости  и  вязкого  газа.  Нестационарная  задача  о  движении  вязкого  газа  изучалась  [4,  с.  365].  В  настоящей  работе  исследуется  полная  система  уравнений  Навье-Стокса  и  Стефана  в  нестационарном  случае,  моделирующая  процесс  испарения  сжимаемой  жидкости.  Доказывается  существование  единственного  приближенного  решения  системы  нестационарных  термодинамических  уравнений,  уравнений  движения  вязкого  газа,  сжимаемой  жидкости  и  свободной  границы  раздела.

Сжимаемая  жидкость  с  плотностью  ,  динамической  вязкостью,  с  коэффициентами  теплопроводности    и  удельной  теплоемкости    находится  в  области  Ω₁,  которая  ограничена  сверху  границей  Г,  а  снизу  границей  .  Вязкий  газ  с  плотностью  ,  с  постоянной  молекулярной  вязкостью  ,  с  коэффициентами  теплопроводности    и  удельной  теплоемкости  с₂  расположен  в  области  Ω₂,  ограниченной  снизу  Г,  а  сверху  .

Свободная  граница  Г  между  жидкостью  и  газом  не  пересекается  с    и.

Скорость  движения  сжимаемой  жидкости  и  вязкого  газа  ,  плотности  жидкости  и  вязкого  газа    и  ,  температура  жидкости  и  газа  ,  перемещение    границы  раздела  сред  Г  в  направлении    нормали  удовлетворяют  нестационарным  уравнениям,  начальным  и  граничным  условиям:

  ,

,

  ,

  (1)

  ,

,                                 (2)

      (3)

где:    —  коэффициент  поверхностного  натяжения, 

H  —  удвоенная  кривизна  Г,

  —  удельная  теплота, 

  и    —  тензоры  напряжений  с  элементами 

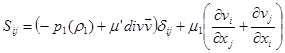
и 

  ,

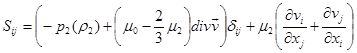  —  непрерывно  дифференцируемые  возрастающие  функции    постоянные  коэффициенты    удовлетворяют  условию  .

Области  ,    можно  продолжить  в  направлении  осей    и    с  периодами    и    соответственно.  Функции    будем  считать  периодическими  с  периодами    и    по    и.

Приближенное  решение  задачи  (1)—(3)  находим  аналогично  приближенному  решению  в  работе  [3,  с.  93].  Обозначим  Т  время  испарения,    шаг  по  времени,    моменты  по  времени,    В  начальный  момент  времени  считаем  известными:

        ,  .

Определим  приближенное  решение  в  момент  времени    при  условии,  что    единственное  приближенное  решение  в  момент  времени  .

Интегрируя  уравнение

,                                               (4)

находим  плотности  жидкости    и  газа 

.

Вектор  скорости    получаем  из  системы  уравнений  Навье-Стокса:

  ,

  ,  (5)

    .

Из  линейной  системы  уравнений  в  известной  области    

,

,,  (6)

    ,

имеем  приближенные  значения  температуры  .

Приближенное  перемещение    свободной  границы    определяем  из  уравнений  (2)  с  заданными  ,.

В  каждый  момент  времени    для  решения  задач  (5),  (6)  применяется  метод  конечного  элемента  аналогично  его  использованию  в  работе  [3,  с.  6].  В  исследовании  задач  (5),  (6)  по  переменной  t  выбирается  разностная  схема  Кренка-Николсона. 

Вводя  непрерывные  функции 

   ,

,  ,

приходим  к  следующему  результату.

Пусть  ,  ,

.

Задача  (1)—(3)  имеет  единственное  приближённое  решение 

.

Если

точное  решение  задачи  (1)—(3),  то 

  в  пространстве  L²  (O,  T;  (L₂  (Ω₂))³),

  в  L²  (O,  T;  L₂(Ω₁Ω₂)),

  в  L²  (O,  T;  (L₂(Г))³).

Список  литературы:

1.Ерунова  И.Б.,  Ривкинд  В.Я..  Исследование  задачи  об  испарении  жидкости  //  Вестник  Ленингр.  университета,  1991,  вып.  2,  №  8.  С.  22—27.

2.Ерунова  И.Б.  Об  оценках  скорости  сходимости  приближенного  расчёта  нестационарного  потока  газа  над  жидкостью  //  Материалы  V  Международной  научно-практической  конференции  «Актуальные  вопросы  науки»,  2012.  —  М.:  «Спутник».  С.  92—95.

3.Erunova  I.,  Neittaanmaki  P.  Convergence  estimates  for  approximation  of  the  steady  flow  liquid  and  gas  over  a  solid.  Report  18,  1997.  —  Jyvaskyla:  University  of  Jyvaskyla.  —  15  p.

4.Solonnikov  V.A.  and  Tani  A..  Free  boundary  problem  for  a  viscous  compressible  flow  with  surface  for  the  stationary  Navier-Stores  system  //  Partial  differential  equations,  Warsaw,  1983,  Vol.  10,  Р.  361—403.