РАССМОТРЕНИЕ  ГРАФА  В  МАТЕМАТИЧЕСКИХ  ПАКЕТАХ  В  КАЧЕСТВЕ  ОБЪЕКТА

Ежова  Марина  Алексеевна

аспирант  УрФУ,  г.  Екатеринбург,  преподаватель  ПФ  МЭСИ,  г.  Пермь

E-mail: 

Пастухова  Галина  Витальевна

аспирант  МПГУ,  г.  Москва,  старший  преподаватель  ПГГПУ,  г.  Пермь

E-mail: 

Граф,  как  его  понимают  математики,  является  достаточно  интересным  и  разносторонним  объектом.  С  одной  стороны  имеются  вполне  конкретные  характеристики  и  свойства,  индивидуальные  для  каждого  конкретного  графа,  но  с  другой  стороны  —  каждый  рисует  граф  в  меру  своих  творческих  способностей.  А  учитывая,  что  все  чаще  идет  обращение  к  математическим  пакетам  (Mathematica,  Maple,  GAP  и  др.)  для  ускорения  процесса  вычисления,  появляется  вопрос:  как  же  пакеты  аналитических  вычислений  представляют  для  себя  граф  и  какие  операции  над  ним  они  поддерживают?

Начнем  с  самого  алгебролизированного  пакета  —  система  компьютерной  алгебры  GAP.  Известно,  что  эта  система,  в  отличие  от  подавляющего  числа  остальных,  была  задумана  именно  как  инстру­мент  комбинаторной  теории  групп,  а  только  после  стала  охватывать  другие  разделы  алгебры,  в  частности  теорию  графов. 

Вспомним,  что  граф  группы  является  одним  из  наглядных  способов  ее  изображения,  иногда  более  эффективный  и  эффектный,  чем  таблица  Кэли,  и  именно  с  этой  позиции  система  GAP  и  рассматривает  графы. 

Пусть  G  —  группа,  имеющая  два  образующих  элемента  a  и  b.  Между  вершинами  P_g  графа  группы  G  и  элементами  g  группы  G  установим  взаимно  однозначное  соответствие.  Пусть  вершины  графа  соединяются  ориентированными  ребрами  двух  типов,  соответствую­щих  образующим  элементам  (например,  два  различных  цвета  D_a  и  D_b),  по  последующему  закону:  если  x  a^-1  =  t,    x  a  =  s,    то  ориентированное  ребро  цвета  D_a  идет

·           к  вершине  P_s  от  вершины  P_x; 

·           к  вершине  P_x  от  вершины  P_t    .

Если  же  x  b^-1  =  v,  x  b  =  u,  то  ориентированное  ребро  цвета  D_b  идет 

·           к  вершине  P_u  от  вершины  P_x; 

·           к  вершине  P_x  от  вершины  P_v. 

Построенную  конструкцию  называю  графом  группы  G,  имеющей  образующие  элементы  a  и  b.  Иначе  «диаграмма  Кэли»,  «групповая  диаграмма»,  «цветная  группа».

В  данный  момент  в  системе  GAP  отсутствуют  инструменты  для  изображения  графа,  но  в  большинстве  случаев  для  решения  задачи  достаточно  бывает  получить  численное  описание.  Для  этого  исполь­зуют  следующие  функции.

Первая  из  них  [4]  дает  возможность  вычислить  список  всех  элементов  группы,  а  также  все  её  порождающие  элементы.  Таким  образом,  получаем  описание  графа  через  список,  каждый  элемент  которого  является  тройкой  чисел  [i,  j,  k],  говорящий,  что  ориентиро­ванное  ребро  цвета  k  проведено  от  i-ой  вершины  к  j-ой  вершине:

Graph:=function(G)

local  elms,  —  список  элементов  группы

gens,  —  список  элементов,  порождающих  группу

graph,  —  описание  графа 

i,  —  номер  элемента  группы

k,  —  номер  цвета  (порождающего  элемента  группы)

j;  —  номер  вершины,  являющейся  концом  ребра,  начинаю­щееся  в  вершине  i,  и  обладающее  цветом  k

elms:=AsSSortedList(G);

gens:=GeneratorsOfGroup(G);

graph:=[];

for  i  in  [1  ..  Length(elms)]  do

for  k  in  [1  ..  Length(gens)]  do

j:=Position(elms,  elms[i]*gens[k]);

Append(graph,  [[i,j,k]]);

od;

od;

return  graph;

end;

В  [4]  указана  вторая  функция,  отображающая  список,  составленный  с  помощью  первой  функции,  как  квадратную  матрицу  порядка  |G|.  В  ней  элемент  a_ij  равен  k,  если  ориентированное  ребро  цвета  k  проведено  от  i-ой  вершины  к  j-ой  вершине,  иначе  —  нулю.  Заметим,  что  подобная  матрица  содержит  достаточно  много  нулевых  элементов,  что  является  неэкономичным  способом  хранения  информации  о  графе  группы.

Рассмотрим  пример  применения  этих  функций  для  описания  графа  симметрической  группы  подстановок  степени  три.  Зададим  группу:

gap>  S:=SymmetricGroup(3);

Sym([1  ..  3])

Выведем  порождающие  элементы  и  элементы  всей  группы  на  экран,  чтобы  в  дальнейшем  уточнять,  как  вершиной  графа  с  соответствующим  номером  соотносится  с  элементом  группы:

gap>  GeneratorsOfGroup(S);

[  (1,2,3),  (1,2)  ]

gap>  AsSSortedList(S);

[  (),  (2,3),  (1,2),  (1,2,3),  (1,3,2),  (1,3)  ]

Получим  описание  графа  группы  через  список:

gap>  t:=Graph(S);

[  [  1,  4,  1  ],  [  1,  3,  2  ],  [  2,  3,  1  ],  [  2,  4,  2  ],  [  3,  6,  1  ],    [  3,  1,  2  ],  [  4,  5,  1  ],  [  4,  2,  2  ],  [  5,  1,  1  ],  [  5,  6,  2  ],  [  6,  2,  1  ],  [  6,  5,  2  ]  ]

Эту  же  информацию  можно  отобразить  в  виде  матрицы,  используя  функцию  Display:

gap>  m:=Mat(t);

[  [  0,  0,  2,  1,  0,  0  ],  [  0,  0,  1,  2,  0,  0  ],  [  2,  0,  0,  0,  0,  1  ],    [  0,  2,  0,  0,  1,  0  ],  [  1,  0,  0,  0,  0,  2  ],  [  0,  1,  0,  0,  2,  0  ]  ]

gap>  Display(m);

[  [0,    0,    2,    1,    0,    0],

[0,    0,    1,    2,    0,    0],

[2,    0,    0,    0,    0,    1],

[0,    2,    0,    0,    1,    0],

[1,    0,    0,    0,    0,    2],

[0,    1,    0,    0,    2,    0]  ]

Граф  (в  общем  случае  ориентированный)  представим  как  список  элементов  (откуда  идет  ребро,  куда  идет  ребро,  какого  цвета  ребро),  который  для  удобства  можно  представить  в  виде  матрицы.

Таким  образом,  граф  как  самостоятельный  объект  для  системы  GAP  не  существует.  Однако  данную  позицию  не  разделяют  другие  математические  пакеты.

Например,  возьмем  систему  Maple  [1].  Как  и  другие  системы,  она  может  выполнять  аналитические  символьные  преобразования,  что  незаменимо  при  решении  задач  на  графах.  К  тому  же  в  Maple  есть  специализированная  система  networks,  составленная  исключительно  из  операторов  для  работы  с  графами.

Неориентированный  граф  изначально  можно  задать  оператором  graph(V,E),  соединяя  тем  самым  множество  вершин  V  (которые  могут  быть  обозначены  числами  или  любым  текстом  в  кавычках:  «my  mother»,  «my  pet»  и  т.  д.)  и  множество  ребер  E.  Можно  использовать  оператор  new(G),  addvertex  (с  указанием  списка  ребер,  инцидентных  вершинам)  и  addedge  (с  указанием  вершин,  принадлежащих  этому  ребру),  создавая  тем  самым  новый  объект  G  —  граф.

Для  него  можно  построить  матрицу  смежности  (A:=adjacency(g)),  узнать  диаметр  самого  графа,  а  также  наличие  эйлеровой  цепи  и  многое  другое.

Интересно,  что  Maple  может  выводить  изображение  графа  на  экран.  В  целом  программа  придерживается  правила:  поместить  все  вершины  на  одну  окружность  (не  всегда  равномерно)  и  соединить  согласно  условию.  Во  многих  случаях  это  можно  принять  за  некий  стандарт  изображения  графа.

С  другой  стороны,  оператор  draw(G)  не  отличает  ориентированный  граф  от  неориентированного  и  рисует  их  одинаково,  т.  е.  без  стрелок.  Конечно,  можно  самостоятельно  дополнить  программу  следующим  текстом:

>restart;

>  Draw1:=proc(S,G)

>  local  q,k,n,n1,m,m1,i,j,t,v,x,y,x1,x2,y1,y2,c,e,E;

>  n1:=nops(S);  #  Задание  число  столбцов  вершин

>  n:=nops(vertices(G)):  #  Задание  число  вершин  графа

>  E:=ends(G):  #  Список  концов  дуг

>  m1:=nops(E):  #  Задание  числа  дуг

>  q:=.5,  2,  .05,  color=green:  #  Выбор  стиля  стрелок

>  for  i  to  n1  do

>  m:=nops(S[i]);  #  Число  вершин  в  столбце  i

>  for  j  to  m  do

>  k:=S[i][j]:  #  Номер  вершины

>  x[k]:=100/n1*i;  y[k]:=100/(m+1)*j;  #  Набор  координат

>  c[k]:=disk([x[k],y[k]],0.5,color=blue):  #  Набор  вершин

>  t[k]:=textplot([x[k]+4,y[k]+1,r[i][j]],  #  Набор  подписей

>  align={ABOVE,RIGHT},font=[TIMES,ITALIC,16]);

>  od;

>  od;

>  for  i  to  m1  do

>  x1:=x[E[i][1]]:  y1:=y[E[i][1]]:  #  Первый  набор  координат

>  x2:=x[E[i][2]]:  y2:=y[E[i][2]]:  #  Второй  набор  координат

>  v[i]:=arrow([x1,y1],[x2,y2],q):  #  Набор  дуг

>  e[i]:=textplot([(x1+x2)/2,(y1+y2)/2+1,e||i],

>  align={ABOVE,RIGHT},#  Набор  подписей  дуг

>  font=[HELVETICA,OBLIQUE,12],color=red);

>  od;

>  display(seq(c[i],i=1..n),seq(t[i],i=1..n),

>  seq(e[i],i=1..m1),seq(v[i],i=1..m1),

>  axes=none,scaling=constrained);

>  end  proc:

>  save  Draw1,  "C:\\SBDISKR\\MAPLE\\draw.m";

И  вот,  что  получится  при  применении  этой  программы: 

>  restart;

>  with(plots):  with(plottools):  with(networks):

>  G:=void(5):  #  Пустой  граф

>  E:=[[1,4],[2,1],[2,3],[3,1],[2,5],  #  Дуги

>  [3,5],[4,3],[4,5]]:

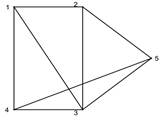
>  addedge(E,G):  r:=[4,1],[3,2],[5]:

>  draw(Linear(r),G);  #  Стандартный  вариант  рисунка

>  read  "C:\\SBDISKR\\MAPLE\\draw.m";

>  Draw1([r],G);  #  Вариант  рисунка  орграфа

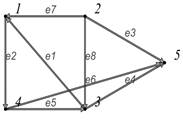
В  данной  системе  граф  не  просто  список  цифр,  а  отдельный  объект.  И  рассматривается  он  не  как  характеристика  какой-нибудь  группы,  именно  как  некое  целое.

Написание  дополнительных  блоков  программы  может  доставить  некоторое  неудобство.  Те,  кто  не  собирается  тратить  время  подобным  образом,  могут  воспользоваться  системой  Mathematica  и  ее  пакетом  дискретной  математики  DiscreteMath.  Там  представлены  4  типа  функций:  представление  графа,  создание  графа,  свойства  графа,  алгоритмическая  теория  графов.  Функции  позволяют  построить  граф,  сходя  из  данного  или  псевдослучайного  списка  вершин  и  ребер,  матрицы  смежности,  характеристики  графа  (полнота,  двоичное  дерево  с  n  уровнями),  а  также  импортируя  изображение  из  файла  или  как  результат  операции  над  уже  известными  графами.  По  уже  построенному  графу  можно  определить  число  и  список  вершин  и  ребер,  степени  вершин  и  ребер,  длину  кратчайшего  пути  между  двумя  вершинами,  цикл,  проходящий  через  все  ребра  или  вершины,  изоморфность  другому  графу,  а  также  имеется  возможность  программирования  действий  на  графе  и  многое  другое.  Именно  системой  Mathematica  дает  наибольшее  из  возможных  разнооб­разий  операций  над  графами,  а  также  над  графическим  представлением.

Можно  сделать  вывод,  что  выбор  математического  пакета  зависит  от  типа  задачи,  которую  предстоит  решать. 

Список  литературы:

1.Кирсанов  М.Н.  Графы  в  Maple.  Задачи,  алгоритмы,  программы:  пособие  по  дискретной  математике  для  студентов  университета.  М.:  Издательство  ФИЗМАТЛИТ,  2007.  —  168  с.

2.Пакет  дискретной  математики  DiscreteMath  /  Сайт  физического  факультета  Белорусского  государственного  педагогического  университета  имени  Максима  Танка.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://phys.bspu.unibel.by/static/lib/inf/cmat/mathem4/gl11/index4.htm  (дата  обращения  07.11.12).

3.Пастухова  Г.В.  Об  одной  проблеме  из  Коуровской  тетради  //  В  мире  научных  открытий,  2010.  №  4  (10),  Часть  11.  С.  17—18.

4.Система  компьютерной  алгебры  GAP  —  примеры  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ukrgap.exponenta.ru/Examples/Graph.htm  (дата  обращения  07.11.12).