Статья опубликована в рамках: I Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 24 декабря 2012 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КОМПЛЕКСНЫЕ, ОГРАНИЧЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Якубовский Евгений Георгиевич
инженер вычислительного центра,
Санкт-Петербургский государственный Горный Университет, г. Санкт-Петербург
E-mail:
Рассмотрим систему нелинейных автономных дифференциальных уравнений
![]() (1)
(1)
Исследуются комплексные и действительные решения задачи Коши этого дифференциального уравнения в случае действительных и комплексных начальных условиях, при действительном аргументе ![]() , т. е.
, т. е. ![]() , где величина
, где величина ![]() соответствует начальному моменту интегрирования, а величина
соответствует начальному моменту интегрирования, а величина ![]() в общем случае комплексная. Причем в случае действительных значениях
в общем случае комплексная. Причем в случае действительных значениях ![]() , правая часть (1) действительна. Рассматривается регулярная правая часть дифференциального уравнения
, правая часть (1) действительна. Рассматривается регулярная правая часть дифференциального уравнения ![]() относительно аргументов
относительно аргументов ![]() , т. е. она представляется сходящимся рядом с положительными целыми степенями
, т. е. она представляется сходящимся рядом с положительными целыми степенями ![]() , т. е. правая часть (1) однозначная функция своих аргументов.
, т. е. правая часть (1) однозначная функция своих аргументов.
Систему дифференциальных уравнений (1) можно представить при не кратных положениях равновесия в виде
![]() , (2)
, (2)
где введен не обращающийся в ноль множитель ![]() , который равен
, который равен ![]() . При подстановке этого множителя в (2), получим (1). Покажем, что этот множитель в ноль не обращается. Величины
. При подстановке этого множителя в (2), получим (1). Покажем, что этот множитель в ноль не обращается. Величины ![]() удовлетворяют условию
удовлетворяют условию ![]() , где величина
, где величина ![]() конечна.
конечна.
При условии ![]() имеем конечный предел
имеем конечный предел
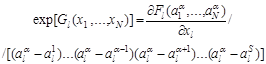 , (3)
, (3)
Где произвели сокращение множителя ![]() , числитель дроби в ноль не обращается, так как рассматриваются не совпадающие корни, являющиеся координатами положения равновесия. При этом если правая часть
, числитель дроби в ноль не обращается, так как рассматриваются не совпадающие корни, являющиеся координатами положения равновесия. При этом если правая часть ![]() дифференциального уравнения не зависит от величины от переменной
дифференциального уравнения не зависит от величины от переменной ![]() не зависит, надо произвести не вырожденное линейное преобразование
не зависит, надо произвести не вырожденное линейное преобразование ![]() и тогда появится зависимость правой части от всех переменных.
и тогда появится зависимость правой части от всех переменных.
При этом дифференциальное уравнение можно записать в виде
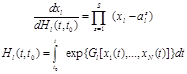 , (4)
, (4)
где: ![]() стремящаяся к бесконечности функция при условии
стремящаяся к бесконечности функция при условии ![]() . В случае решения в действительной плоскости это монотонная функция.
. В случае решения в действительной плоскости это монотонная функция.
Решением дифференциального уравнения (2) является функция ![]() , удовлетворяющая формуле (5). Для получения (5) разделим уравнение (4) на произведение множителей
, удовлетворяющая формуле (5). Для получения (5) разделим уравнение (4) на произведение множителей ![]() и умножим (4) на величину
и умножим (4) на величину ![]() . Раскладываем полученную дробь на сумму простых дробей и их интегрируем. Потенцируя полученное выражение, получим (5)
. Раскладываем полученную дробь на сумму простых дробей и их интегрируем. Потенцируя полученное выражение, получим (5)
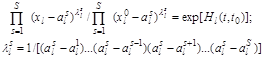 , (5)
, (5)
где все значения координат положения равновесия не одинаковы.
Теорема 1. При решении задачи Коши для системы (1), а значит и решение системы (5) величина ![]() при условии
при условии ![]() . Правую часть (1) считаем регулярными функциями по своим аргументам. Т. е. она либо представляется сходящимся рядом, либо является полиномом многих переменных. Она имеет конечное число не кратных положений равновесия. Она действительна при действительных
. Правую часть (1) считаем регулярными функциями по своим аргументам. Т. е. она либо представляется сходящимся рядом, либо является полиномом многих переменных. Она имеет конечное число не кратных положений равновесия. Она действительна при действительных ![]() . Задача Коши для системы дифференциальных уравнений (1) определяется при комплексных начальных условиях
. Задача Коши для системы дифференциальных уравнений (1) определяется при комплексных начальных условиях ![]() , где
, где ![]() возможно комплексное число. При этом аргументы в правой части формулы (1) будут комплексные, и дифференциальное уравнение будет комплексное, но однозначная функция своих аргументов, при действительном параметре
возможно комплексное число. При этом аргументы в правой части формулы (1) будут комплексные, и дифференциальное уравнение будет комплексное, но однозначная функция своих аргументов, при действительном параметре ![]() .
.
Доказательство.
Если при росте времени до бесконечности величина ![]() имеет конечный предел, то имеем формулу
имеет конечный предел, то имеем формулу ![]() . Вычислим спектр сигнала в комплексной плоскости, так как придется интегрировать по комплексной переменной, устремив
. Вычислим спектр сигнала в комплексной плоскости, так как придется интегрировать по комплексной переменной, устремив ![]() .
.
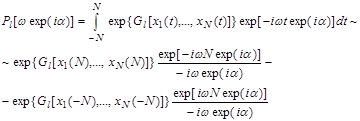
При вычислении последнего интеграла использован вклад граничных точек.
При этом получаем, что интеграл по действительной оси равен вычету в нулевой точке плюс интеграл по дуге окружности с бесконечным радиусом ![]() в верхней полуплоскости
в верхней полуплоскости
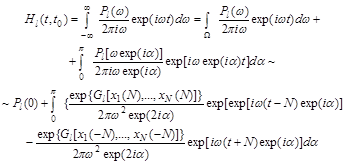
При этом контур ![]() соответствует обходу снизу нулевой точки
соответствует обходу снизу нулевой точки ![]() , и интеграл соответствует вычету в этой точке. При этом величина
, и интеграл соответствует вычету в этой точке. При этом величина ![]() стремится к бесконечности
стремится к бесконечности ![]() , при условии
, при условии ![]() в силу роста одного из членов на минус бесконечности
в силу роста одного из членов на минус бесконечности ![]() , или плюс бесконечности
, или плюс бесконечности ![]() , так как второй интеграл от нуля до
, так как второй интеграл от нуля до ![]() считается при условии
считается при условии ![]() .
.
Конец доказательства.
Теорема 2. Решение системы уравнений (5), а, следовательно, и решение задачи Коши для системы (1) в комплексной плоскости с комплексными начальными условиями конечно на действительном отрезке ![]() . Правую часть (1) считаем регулярной функцией, заданной сходящимся рядом или полиномом по своим аргументам. Она имеет конечное число не кратных положений равновесия. Она действительна при действительных
. Правую часть (1) считаем регулярной функцией, заданной сходящимся рядом или полиномом по своим аргументам. Она имеет конечное число не кратных положений равновесия. Она действительна при действительных ![]() . Задача Коши для системы дифференциальных уравнений (1) определяется при комплексных начальных условиях
. Задача Коши для системы дифференциальных уравнений (1) определяется при комплексных начальных условиях ![]() , где
, где ![]() возможно комплексное число. При этом аргументы в правой части формулы (1) будут комплексные, и дифференциальное уравнение будет комплексное, при действительном параметре
возможно комплексное число. При этом аргументы в правой части формулы (1) будут комплексные, и дифференциальное уравнение будет комплексное, при действительном параметре ![]() .
.
Доказательство. Сумма коэффициентов ![]() по индексу
по индексу ![]() равна нулю, т. е.
равна нулю, т. е. ![]() . Для доказательства этого тождества рассмотрим полином
. Для доказательства этого тождества рассмотрим полином ![]() степени относительно
степени относительно ![]()
![]() ,
,
В точках положения равновесия ![]() полином удовлетворяет
полином удовлетворяет ![]() . В силу единственности полинома степени
. В силу единственности полинома степени ![]() , проходящего через
, проходящего через ![]() точек, получаем
точек, получаем ![]() , так как это значение удовлетворяет точкам аппроксимации. Распишем формулу для полинома, равного единице, разделив его на произведение
, так как это значение удовлетворяет точкам аппроксимации. Распишем формулу для полинома, равного единице, разделив его на произведение ![]() , получим
, получим
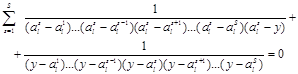 ,
,
полагая, ![]() получим тождество
получим тождество ![]() , в случае, если имеется
, в случае, если имеется ![]() положение равновесия.
положение равновесия.
Допустим, выполняется условие ![]() . Тогда левая часть (5) стремится к конечному значению, так как
. Тогда левая часть (5) стремится к конечному значению, так как ![]() , т. е.
, т. е. ![]() . Но согласно теореме 1 величина
. Но согласно теореме 1 величина ![]() не ограничена. Т. е. допущение о бесконечности решения привело к противоречию, значит решение
не ограничена. Т. е. допущение о бесконечности решения привело к противоречию, значит решение ![]() конечно на любом отрезке
конечно на любом отрезке ![]() .
.
Конец доказательства.
Теорема 3. Рассматривается задача Коши при произвольных действительных начальных условиях для системы нормальных нелинейных обыкновенных дифференциальных уравнений (1). Случай вырожденного решения задачи Коши – положения равновесия, не рассматривается. В случае, если у системы (1) имеются комплексно-сопряженные положения равновесия, то при конечном аргументе ![]() действительное решение задачи Коши системы (1) при действительных начальных условиях стремится к бесконечности, а потом переходит в комплексное решение, в случае, если все положения равновесия комплексные. При этом правую часть (1) считаем регулярной функцией. Она имеет конечное число не кратных положений равновесия.
действительное решение задачи Коши системы (1) при действительных начальных условиях стремится к бесконечности, а потом переходит в комплексное решение, в случае, если все положения равновесия комплексные. При этом правую часть (1) считаем регулярной функцией. Она имеет конечное число не кратных положений равновесия.
Доказательство.
Если решать систему (2) в действительной плоскости при не кратных положениях равновесия, то получим
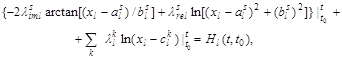 , (6)
, (6)
где: ![]() выделенное комплексное положение равновесия,
выделенное комплексное положение равновесия,
![]() остальные положения равновесия. Коэффициенты
остальные положения равновесия. Коэффициенты ![]() удовлетворяют
удовлетворяют ![]() . При этом в сумме
. При этом в сумме ![]() величина действительной части
величина действительной части ![]() в случае комплексного значения
в случае комплексного значения ![]() участвует дважды и в силу того, что все числа
участвует дважды и в силу того, что все числа ![]() удовлетворяют условию
удовлетворяют условию ![]() , имеем формулу
, имеем формулу ![]() .
.
Обоснуем формулу (6). Для этого два комплексно сопряженных члена решения преобразуем (для упрощения записи индекс ![]() опускаем)
опускаем)
![]() , (7)
, (7)
где ![]() . После интегрирования (7) по аргументу
. После интегрирования (7) по аргументу ![]() , получим формулу (6)
, получим формулу (6)
![]() .
.
Решение равняется
![]() ,
,
где
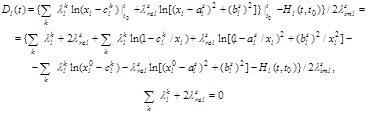 .
.
При этом величина ![]() действительная в силу существования комплексно-сопряженных положений равновесия. Т. е. имеем равенство при условии
действительная в силу существования комплексно-сопряженных положений равновесия. Т. е. имеем равенство при условии ![]()
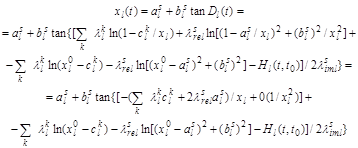 . 8)
. 8)
Это уравнение имеет решение, стремящееся к бесконечности при условии
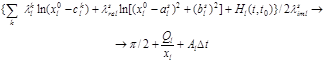 (9)
(9)
Подставляя формулу (13) в формулу (12), получим
![]() .
.
При этом, это уравнение имеет решение ![]() , так как сводится к тождеству
, так как сводится к тождеству
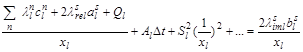 .
.
Это уравнение определяет бесконечное решение, которое меняет знак бесконечности справа от координаты бесконечности.
При этом решение дифференциального уравнения при росте ![]() может иметь комплексные корни
может иметь комплексные корни
![]() .
.
При этом, так как справедливо ![]() имеются числа с отрицательной действительной частью
имеются числа с отрицательной действительной частью ![]() , значит неизвестная функция будет стремиться к одному из положений равновесия, чтобы обеспечить бесконечность правой части. Значит, если все положения равновесия комплексные получается конечное комплексное решение при условии бесконечности
, значит неизвестная функция будет стремиться к одному из положений равновесия, чтобы обеспечить бесконечность правой части. Значит, если все положения равновесия комплексные получается конечное комплексное решение при условии бесконечности ![]() . Т. е. в промежуточной точке начнется комплексное решение. При этом действительное решение устремится к бесконечности, будут нарушены условия существования и единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений и возникнет комплексное решение.
. Т. е. в промежуточной точке начнется комплексное решение. При этом действительное решение устремится к бесконечности, будут нарушены условия существования и единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений и возникнет комплексное решение.
Конец доказательства.
Приведем пример, описывающий это свойство дифференциального уравнения, переход к комплексному решению. Так для дифференциального уравнения может возникнуть комплексное решение, вместо бесконечного действительного решения
![]() .
.
Причем положения равновесия чисто мнимые ![]() , и значит, решение может не стремиться к положению равновесия.
, и значит, решение может не стремиться к положению равновесия.
Используя неявную схему решения, получим следующее уравнение
![]() .
.
Разрешая относительно неизвестной функции ![]() , получим неявную схему
, получим неявную схему
![]() .
.
Которое при условии ![]() определит конечное комплексное решение.
определит конечное комплексное решение.
Теорема 4. Для обязательного существования конечного точного решения нелинейных уравнений в частных производных типа (14) необходимо использовать комплексное решение.
Доказательство.
Рассмотрим уравнение в частных производных
![]() (10)
(10)
решение ищем в виде
![]() . (11)
. (11)
Сходимость ряда (11) при условии ![]() доказывается в каждом отдельном случае с помощью численного эксперимента.
доказывается в каждом отдельном случае с помощью численного эксперимента.
Подставим в уравнение (10) функцию (11), умножим уравнение (10) на величину ![]() , где величина произведений этих функций является интегрируемой по пространству и все эти функции независимы, и проинтегрируем по всему пространству, уравнение (6) может быть сведено к системе уравнений
, где величина произведений этих функций является интегрируемой по пространству и все эти функции независимы, и проинтегрируем по всему пространству, уравнение (6) может быть сведено к системе уравнений
![]() (12)
(12)
Рассмотрим случай, когда правая часть (12) является сходящейся функцией, возможно с конечным числом членов. Конечное число членов получается, если коэффициента квазилинейной системы уравнений в частных производных являются полиномом от неизвестной функции ![]() . Где при комплексных положениях равновесия системы уравнений (12), действительное решение
. Где при комплексных положениях равновесия системы уравнений (12), действительное решение ![]() стремится к бесконечности, а комплексное решение конечно, аналогично решению системы (1).
стремится к бесконечности, а комплексное решение конечно, аналогично решению системы (1).
При этом необходимо сказать, что имеет конечное значение точное комплексное решение и может оказаться, что в случае разных на порядки решений дифференциального нелинейного уравнения приближенное решение, считаемое с помощью ЭВМ, может стремиться к бесконечности, как решение жесткого обыкновенного дифференциального уравнения.
Покажем, что и величина ![]() стремится к бесконечности, в случае бесконечных коэффициентов
стремится к бесконечности, в случае бесконечных коэффициентов ![]() . Для этого умножим величину (11) на
. Для этого умножим величину (11) на ![]() , и проинтегрируем по пространству, получим
, и проинтегрируем по пространству, получим
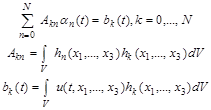 .
.
Допустим, величина ![]() конечна. Тогда и величина коэффициентов
конечна. Тогда и величина коэффициентов ![]() конечна. В силу независимости функции
конечна. В силу независимости функции ![]() и конечности интегралов, равных
и конечности интегралов, равных ![]() , определитель матрицы Грамма
, определитель матрицы Грамма ![]() не вырожден (см. [1]), причем величины
не вырожден (см. [1]), причем величины ![]() являются векторами со скалярным произведением в виде интеграла по пространству. Но тогда в силу предположения конечность коэффициентов
являются векторами со скалярным произведением в виде интеграла по пространству. Но тогда в силу предположения конечность коэффициентов ![]() , конечны и коэффициенты
, конечны и коэффициенты ![]() . В случае бесконечных коэффициентов
. В случае бесконечных коэффициентов ![]() , бесконечны и коэффициенты
, бесконечны и коэффициенты ![]() .
.
Итак, показано, что для комплексных значений положения равновесия системы дифференциальных уравнений (12), точное решение уравнения в частных производных бесконечно в действительной плоскости и конечно в комплексной плоскости.
Отсюда вывод, решение нелинейного уравнения в частных производных при любом способе решение могут стремиться к бесконечности, а при комплексном решении имеют конечное решение.
Конец доказательства.
Отметим, что необходимость комплексного решения следует из решения нелинейных дифференциальных уравнений.
Физическим смыслом комплексного свободного решения, без наложения связей, в декартовом ![]() мерном пространстве, является возникновение вращения траектории. Возникающее вращательное движение при свободном движении частицы является свойством нелинейных систем, когда скорость движения входит в уравнение нелинейно. Этим возникающим вращательным движением в потоке является турбулентность. Причем как показано в разделе 4. комплексное решение определяет средние величины в потоке, действительная часть решения среднюю скорость, а мнимая часть решения определяет среднеквадратичное отклонение скорости при действительных начальных условиях. При этом мнимая часть решения имеет другой физический смысл, она описывает среднее вращение жидкости. Т. е. комплексное решение описывает среднюю скорость в потоке при комплексных начальных условиях.
мерном пространстве, является возникновение вращения траектории. Возникающее вращательное движение при свободном движении частицы является свойством нелинейных систем, когда скорость движения входит в уравнение нелинейно. Этим возникающим вращательным движением в потоке является турбулентность. Причем как показано в разделе 4. комплексное решение определяет средние величины в потоке, действительная часть решения среднюю скорость, а мнимая часть решения определяет среднеквадратичное отклонение скорости при действительных начальных условиях. При этом мнимая часть решения имеет другой физический смысл, она описывает среднее вращение жидкости. Т. е. комплексное решение описывает среднюю скорость в потоке при комплексных начальных условиях.
Теорема 5. В ![]() мерном случае, восстановить комплексный вектор
мерном случае, восстановить комплексный вектор ![]() , у которого действительная и мнимая часть ортогональны, по комплексному вектору
, у которого действительная и мнимая часть ортогональны, по комплексному вектору ![]() , у которого действительная и мнимая часть не ортогональна, надо с помощью формулы
, у которого действительная и мнимая часть не ортогональна, надо с помощью формулы
![]() .
.
Причем эта формула удовлетворяет ![]() . Причем надо отметить, что функции
. Причем надо отметить, что функции ![]() расположены в разных
расположены в разных ![]() мерных пространствах, а функция
мерных пространствах, а функция ![]() построена для одного пространства, в котором действительная и мнимая часть ортогональны.
построена для одного пространства, в котором действительная и мнимая часть ортогональны.
Доказательство.
Вектора действительной и мнимой части должны быть ортогональны, как на двумерной плоскости, так и в ![]() мерном пространстве. Преобразовать их, это значит построить из действительного и мнимого не ортогонального вектора, два ортогональных вектора.
мерном пространстве. Преобразовать их, это значит построить из действительного и мнимого не ортогонального вектора, два ортогональных вектора.
Причем считаем, что функции ![]() заданы в одинаковых пространствах
заданы в одинаковых пространствах
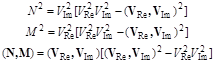 .
.
Покажем, что векторы ![]() ортогональны. Для этого составим скалярное произведение этих векторов
ортогональны. Для этого составим скалярное произведение этих векторов
![]() .
.
При этом действительный вектор в действительном пространстве, соответствующий комплексному вектору ![]() , равен
, равен ![]() .
.
При этом комплексные вектора ![]() получаются в результате решения нелинейных уравнений в частных производных, сводящихся к обыкновенным нелинейным дифференциальным уравнениям, а комплексный вектор
получаются в результате решения нелинейных уравнений в частных производных, сводящихся к обыкновенным нелинейным дифференциальным уравнениям, а комплексный вектор ![]() построен, и удовлетворяет основному свойству комплексных векторов, его действительная и мнимая часть ортогональны.
построен, и удовлетворяет основному свойству комплексных векторов, его действительная и мнимая часть ортогональны.
Список литературы:
1. Гантмахер Ф.Р. Теория матриц М.: «Наука», 1988. — 552 с.
дипломов


Комментарии (1)
Оставить комментарий