ИССЛЕДОВАНИЕ ВЛИЯНИЯ УГЛА РАСПЫЛА НА ПРОЦЕСС ГОРЕНИЯ ДВУХ ВИДОВ ТОПЛИВ ПРИ ВЫСОКИХ ДАВЛЕНИЯХ

Аскарова Алия Сандыбаевна

д-р физ.-мат. наук, профессор

Казахский национальный университет имени аль-Фараби, г. Алматы

Болегенова Салтанат Алихановна

д-р физ.-мат. наук, профессор

Казахский национальный университет имени аль-Фараби, г. Алматы

Березовская Ирина Эдуардовна

PhD, старший преподаватель

Казахский национальный университет имени аль-Фараби, г. Алматы

Максимов Валерий Юрьевич

PhD докторант, преподаватель

Казахский национальный университет имени аль-Фараби, г. Алматы

Оспанова Шынар Сабитовна

PhD докторант, преподаватель

Казахский национальный университет имени аль-Фараби, г. Алматы

E-mail: shinar_ospanova87@mail.ru

Данная статья посвящена актуальной проблеме теплофизики — определение оптимальных параметров сжигания жидкого топлива в камере сгорания. В настоящее время, основным источником вырабатываемой энергии остается энергия различных типов топлив, несмотря на то, что применение ядерной энергии в промышленно развитых странах расширяется, а методы использования энергии солнца, ветра и приливов интенсивно разрабатываются. Ограниченность ресурсов топлива приводит к необходимости организации более экономичных способов его сжигания [5, с. 344].

Горение жидких топлив отличается рядом специфических особенностей, обусловленных протеканием химических реакций в условиях динамического и теплового взаимодействия реагентов, интенсивного массопереноса при фазовых превращениях, а также зависимостью параметров процесса, как от термодинамического состояния системы, так и от ее структурных характеристик.

Так как исследование горения невозможно без его детального изучения, то на первый план выходит проблема фундаментального исследования закономерностей процессов тепломассопереноса при сжигании различных топлив.

Численное исследование горения жидких топлив является сложной задачей теплофизики, так как требует учета большого количества взаимосвязанных процессов и явлений. Поэтому вычислительный эксперимент становится все более важным элементом исследования процессов горения и проектирования различных устройств, использующих процесс горения. Можно с уверенностью говорить, что его роль будет возрастать и в дальнейшем. Поэтому все большее распространение в теплофизике получают методы вычислительной гидродинамики, поскольку появляется возможность оптимизировать эксперимент на основе его виртуального прототипа.

К настоящему времени становится все более ясным, что все проблемы, возникающие в аэро- и гидродинамике при численном решении уравнений Навье-Стокса, вряд ли будут решены. Поэтому в связи со всевозрастающим применением численных исследований при решении научно-технических задач важно обеспечить как можно большую научную и практическую «жатву». Это возможно лишь при условии глубокого проникновения методов математического моделирования в ту или иную предметную область.

Решение задачи о распылении и горении жидкого топлива осуществляется методами численного моделирования с использованием дифференциальных уравнений, описывающих турбулентное течение при наличии химических реакций, и представлены основными уравнениями: неразрывности, движения, внутренней энергии, k-ε модель турбулентности, а так же начальными и граничными условиями.

Уравнение неразрывности для компоненты реакции m имеет вид:

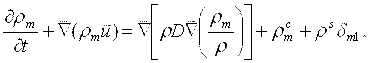                               (1)

где D — коэффициент диффузии, r_m — массовая плотность жидкой фазы, r — полная массовая плотность,  — химический источниковый член;  — источниковый член вследствие впрыска; u— скорость жидкости.

Уравнение неразрывности для жидкости, имеет следующий вид:

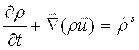_.                                                (2)

Уравнение движения для смеси жидкостей:

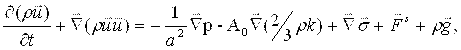                       (3)

где р — давление жидкости, a - безразмерная величина,  A₀ равно 0 при ламинарном течении и 1 — при турбулентности. Тензор вязких напряжений имеет вид:

                                (4)

Здесь µ — динамическая вязкость жидкости,  — коэффициент вязкости, g — ускорение свободного падения и I — удельная внутренняя энергия.

Уравнение внутренней энергии представлено ниже:

,     (5)

где — источниковый член, обусловленный тепловыделением в результате химической реакции и  — тепло, которое приносит впрыскиваемое топливо. Вектор теплового потока J складывается из электропроводности и переноса энтальпии.

При использовании модели турбулентности (А₀=1) решаются уравнения для кинетической энергии турбулентности k и скорости ее диссипации ε :

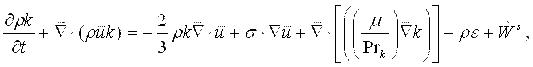  (6)

              (7)

Величина  возникает вследствие взаимодействия с распылителем. Константы  определяются из эксперимента [3, с. 7—9].

На основном участке развития струи процессы испарения и смесеобразования распыленного топлива протекают более интенсивно. При мало изменяющемся угле раскрытия струи возрастает ее боковая поверхность по мере удаления от распылителя форсунки. При впрыскивании в цилиндр двигателя топливной струи с небольшим углом рассеивания ее боковая поверхность уменьшается, что приведет к уменьшению количества испарившегося топлива за период задержки воспламенения. Изменение величины угла рассеивания топливной струи позволяет интенсифицировать “закрутку” воздушного заряда что, в итоге, положительно отразится на топливной экономичности двигателя [2, с. 758—761].

При высоких давлениях рабочей смеси, топлива с окислителем, используется дизельное топливо. Топливо воспламеняется за счет температуры рабочей смеси при высоком давлении. Вследствие этого, характерной особенностью дизельных двигателей является отсутствие системы воспламенения топлива. Основной характеристикой дизельного топлива является цитановое число. Оно характеризует процентное содержание цитана в смеси эталонного топлива. В качестве компонента дизельного топлива используется додекан C₁₂H₂₆.

Основным химическим свойством предельных углеводородов, определяющих их использование в качестве топлива, является реакция горения. В общем случае уравнение реакции горения для любого углеводорода C_xH_y, можно записать в следующем виде: C_xH_y+(x+0,25y)O₂→xCO₂+0,5yH₂O.

В настоящей работе использовали два вида жидкого топлива: октан (C₈H₁₈) и додекан (C₁₂H₂₆). Химические реакции для этих двух видов топлив представлены ниже:

2С₈Н₁₈+50О₂=16СО₂+18Н₂О,                                                      

2С₁₂Н₂₆+37О₂=24СО₂+26Н₂О                                                       (8)

В данной работе с использованием стохастической математической модели (описанной в работе [4, с. 254—261]), проводилось исследование угла распыла α от 2⁰ до 14⁰ при оптимальных значениях давления (Р) и массы (m), которые определены в работе [1, с. 219], для октана Р=100 бар и m=6 мг и для додекана Р=80 бар и m=7 мг. Жидкое топливо при температуре 298 К распыляется через сопло, расположенное в центре основания цилиндрической камеры высотой 15 см и радиусом 2 см. Топливо, впрыскиваемое в камеру сгорания, которая заполнена воздухом при температуре 800 К, проходит процесс быстрого испарения и сгорает в газовой фазе. Процесс горения жидкого топлива в среднем занимает 4 мс. Время распыления жидкого топлива равно 1.4^.10^-3 с. Количество контрольных ячеек — 600. Температура стенок камеры сгорания равна 353 К. Площадь сопла инжектора составляет 2·10^-4 см².

На рисунках 1—3 представлены результаты вычислительного эксперимента по влиянию угла распыла жидкого топлива на распределение температуры в камере сгорания, образования концентрации углекислого газа и топлива.

Анализ рис. 1 показывает, что при увеличении угла распыла от 2⁰ до 10⁰ температура в камере сгорания монотонно повышается для обоих топлив. Максимальная температура в камере сгорания 1964 К для октана и 1991 К для додекана достигается при α равном 10⁰ . При дальнейшем увеличении α, для октана изменение температуры не наблюдается, а для додекана имеет место незначительное понижение температуры.

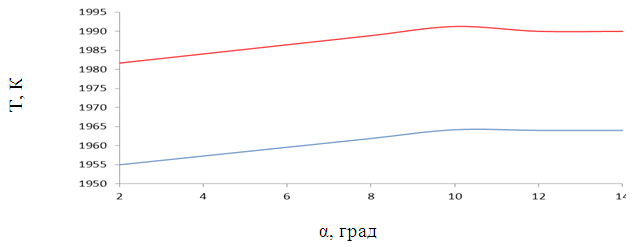
Рисунок 1. Распределение температуры в камере сгорания в зависимости от значения угла распыла α (синяя линия — октан (С₈Н₁₈) при Р=100 бар,

красная линия — додекан (С₁₂Н₂₆) при Р=80 бар)

На рис. 2 изображена зависимость концентрации СО₂ от значения угла распыла. Из рисунка 2 видно, что с увеличением угла распыления октана от 20⁰ до 100⁰ выделяется небольшое количество углекислого газа, которое соответствует значениям концентрации от 0,1007 г/г до 0,1008 г/г, а для додекана от 0,1019 г/г до 0,1022 г/г. Дальнейшее увеличении α практически не меняет величины СО₂ в камере сгорания для обоих топлив.

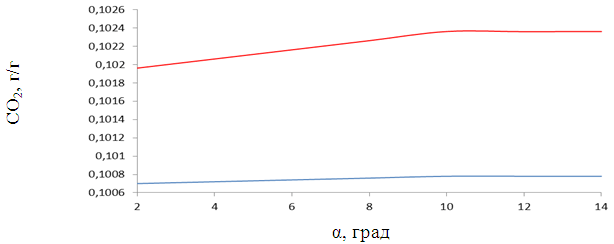
Рисунок 2. Распределение концентрации СО₂ в камере сгорания в зависимости от значения угла распыла α (синяя линия — октан (С₈Н₁₈) при Р=100 бар, красная линия — додекан (С₁₂Н₂₆) при Р=80 бар)

Для обоих топлив небольшое количество углекислого газа (рис. 2) выделяется при максимальной температуре в камере сгорания (рис. 1), что можно использовать для более выгодной организации процесса горения жидкого топлива.

Как показывают кривые на рис. 3 с увеличением угла распыления от 20⁰ до 100⁰ концентрация обоих видов топлив уменьшается. При значении более 100⁰ — концентрация топлива практически не меняется, что согласуется с предыдущим результатом, изображенном на рис. 2. Для октана наблюдается практически линейная зависимость концентрации топлива в камере сгорания и концентрации образующегося в результате горения топлива углекислого газа от угла распыления.  

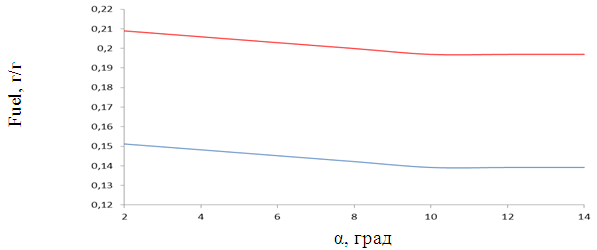
Рисунок 3. Распределение концентрации топлива в зависимости от значения угла распыла α (синяя линия — октан (С₈Н₁₈) при Р=100 бар,

красная линия — додекан (С₁₂Н₂₆) при Р=80 бар)

В условиях данной задачи, при оптимальных значениях давления в камере сгорания и массы топлива, для лучшей организации процесса горения октана и додекана применительно к углу распыления установлено, что наиболее эффективно процесс горения двух топлив протекает при значении угла распыла 100⁰, когда температура в камере сгорания прогревается до максимальных значений 1964 К для октана и 1991 К для додекана, топливо сгорает без остатка, а концентрация углекислого газа незначительна и не превышает значения предельно допустимой концентрации вредных веществ.

Список литературы:

1.Аскарова А.С., Болегенова С.А., Березовская И.Э., Рыспаева М.Ж., Максимов В.Ю. Численное моделирование влияния массы впрыска октана и додекана при высоких давлениях на процесс горения в камере сгорания при высоких давлениях // Матер. VII Между. науч.-практ. конф. «Образование, наука, инновации — вклад молодых исследователей». — Кемерово, 2012. — с. 758—761.

2.Витман Л.А., Кацнельсон Б.Д., Палеев И.И. под ред. Кутателадзе С.С. Распыливание жидкости форсунками. М.: Государственное энергетическое издательство, 1962. 265 с.

3.Amsden A.A., O'Rourke P.J., Butler T.D. KIVA-II: A computer program for chemically reactive flows with sprays. — Los Alamos, 1989. — 160 р.

4.Gorokhovski M., Chtab-Desporter A., Voloshina I., Askarova A. Stochastic simulation of the spray formation assisted by a high pressure // Proceed. of 6th Internat. Symposium on Multiphase Flow, Heat mass transfer and energy conversion. — Xi’an, 2009. — P. 254—261.

5.Vinkovic I, Simoens S., Gorokhovski M. Large eddy simulation of droplet dispersion for inhomogeneous turbulent wall flow // Int. J. of Multiphase Flow. — Vol. 32, № 3, 2005. P. 344—364.