Статья опубликована в рамках: VIII Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 26 ноября 2012 г.)
Наука: Математика
Секция: Теория вероятностей и математическая статистика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
УПРОЩЕНИЕ КРИТЕРИЯ АКАИКЕ ДЛЯ ГИСТОГРАММЫ
Бардасов Сергей Александрович
канд. физ.-мат. наук, доцент ТюмГУ, г. Тюмень
E-mail: sbard@mail.ru
Одной из основных идей в статистике является понятие функции плотности распределения (плотности вероятности) ![]() . В связи с этим важной является проблема ее оценки. Для этого широко используется гистограмма. При ее построении необходимо определить число интервалов (групп), на которые будет разбита выборочная совокупность.
. В связи с этим важной является проблема ее оценки. Для этого широко используется гистограмма. При ее построении необходимо определить число интервалов (групп), на которые будет разбита выборочная совокупность.
Согласно информационному критерию Акаике число групп ![]() должно быть таким, чтобы минимизировать выражение
должно быть таким, чтобы минимизировать выражение
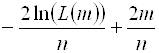 , (1)
, (1)
где ![]() — объем выборки,
— объем выборки, ![]() — функция правдоподобия. Использование коэффициента 2 в формуле (1) является общепринятым (так сложилось исторически).
— функция правдоподобия. Использование коэффициента 2 в формуле (1) является общепринятым (так сложилось исторически).
Функция правдоподобия для гистограммы имеет вид
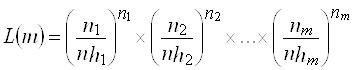 ,
,
где ![]() количество выборочных значений переменной в
количество выборочных значений переменной в ![]() ой группе;
ой группе;
![]() длина
длина ![]() го интервала гистограммы. При определении функции правдоподобия полагаем, что не должно быть пустых групп и групповых интервалов, равных нулю.
го интервала гистограммы. При определении функции правдоподобия полагаем, что не должно быть пустых групп и групповых интервалов, равных нулю.
В случае равных интервалов, имеем:

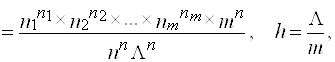
где ![]() — размах вариации.
— размах вариации.
Натуральный логарифм функции правдоподобия равен:
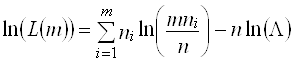 (2)
(2)
Не принимая в расчет величины, независящие от числа групп ![]() , подставим (2) в (1), поменяем знак и разделим на 2. Получим, что в случае равных интервалов, оптимальное число групп
, подставим (2) в (1), поменяем знак и разделим на 2. Получим, что в случае равных интервалов, оптимальное число групп ![]() равно:
равно:
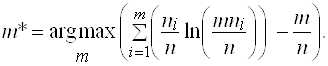 (3)
(3)
Приступим к упрощению критерия (3). Рассмотрим слагаемые
 .
.
Очевидно, что при большом объеме выборки ![]() , значения
, значения  мало отличаются от 1. Оставляя первое слагаемое в разложении логарифма в ряд Тейлора, получим:
мало отличаются от 1. Оставляя первое слагаемое в разложении логарифма в ряд Тейлора, получим:
 .
.
Известны следующие неравенства [1, с. 24]
 (4)
(4)
справедливые при ![]() . Равенства имеет место только при
. Равенства имеет место только при ![]() . В предельных случаях
. В предельных случаях ![]() и
и ![]() при всех
при всех ![]() :
:
![]() .
.
С ростом объема выборки и числа интервалов гистограммы отношение ![]() стремится к нулю. Проведем следующую замену:
стремится к нулю. Проведем следующую замену:
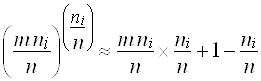 .
.
Тогда
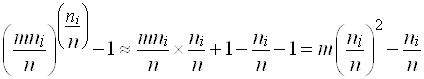 ,
,
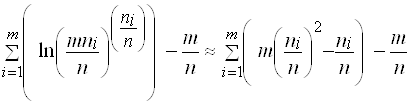 .
.
Отбрасывая независящее от числа групп слагаемое 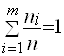 , получим следующий критерий:
, получим следующий критерий:
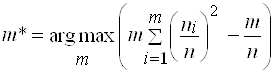 . (5)
. (5)
Пусть истинная функция плотности распределения имеет вид (линейное распределение):
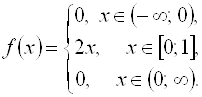 (6)
(6)
Применим критерий (5) к функции плотности вероятностей (6). Разделим отрезок ![]() на
на ![]() частей, тогда
частей, тогда
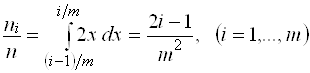 .
.
В этом случае сумма квадратов относительных частот может быть легко вычислена:
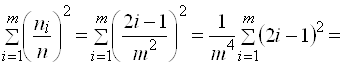
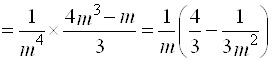 .
.
Тогда
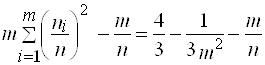
Найдем производную последнего выражения по ![]() и приравняем ее к нулю
и приравняем ее к нулю
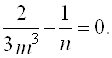
Следовательно, согласно критерию (5) оптимальное число интервалов равно
 . (7)
. (7)
В работе [3, с. 605] Д. Скотт для оценки длины интервала гистограммы минимизировал интегральную среднеквадратическую ошибку
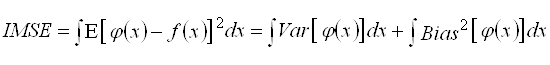 ,
,
где ![]() — точечная дисперсия,
— точечная дисперсия, ![]() — точечное смещение,
— точечное смещение, ![]() — символ математического ожидания.
— символ математического ожидания.
В работе [2, с. 605] Д. Скотт для оценки длины интервала гистограммы минимизировал интегральную среднеквадратическую ошибку
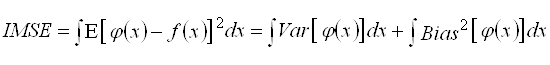 ,
,
где ![]() — символ математического ожидания,
— символ математического ожидания, ![]() — оценка истинной функции плотности вероятности
— оценка истинной функции плотности вероятности ![]() ,
, ![]() — точечная дисперсия,
— точечная дисперсия, ![]() — точечное смещение. Согласно формуле Скотта [2, с. 607] для плотности (6) получим тот же результат:
— точечное смещение. Согласно формуле Скотта [2, с. 607] для плотности (6) получим тот же результат:
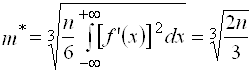 .
.
Таким образом, непараметрический критерий (5), полученный упрощением критерия Акаике, по крайней мере, для функции плотности распределения (6) рекомендует число групповых интервалов, совпадающее с формулой Скотта.
Стоун [3] минимизировал выражение
![]()
и получил, что для определения оптимальной длины интервала гистограммы необходимо минимизировать величину
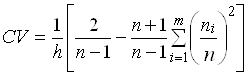 . (8)
. (8)
Похожее правило получил Рудемо [4], который использовал метод кросс-валидации (перекрестной оценки) и риск-функцию Кульбака-Лейблера. Формула (8) дает число групп в ![]() раз меньшее по сравнению с (5).
раз меньшее по сравнению с (5).
Список литературы:
1.Беккенбах Э., Беллман Р. Неравенства. М.: Мир, 1964. — 276 с.
2.Scott D.W. On optimal and data-based histograms // Biometrika. — 1979. — Vol. 66. — P. 605—610.
3.Stone C.J. An asymptotically histogram selection rule. Proc. Second Berkeley Symp (ed. J. Neyman). — 1984. — P. 513—520. Berkeley: Univ. California Press.
4.Rudemo M. Empirical choice of histograms and kernel density estimators // Scand. J. Statist. — 1982. —Vol. 9, P. 65—78.
дипломов

Оставить комментарий