ОПТИМАЛЬНОЕ ЧИСЛО ИНТЕРВАЛОВ ГИСТОГРАММЫ

Бардасов Сергей Александрович

канд. физ.-мат. наук, доцент ТюмГУ, г. Тюмень

E-mail: sbard@mail.ru

Одной из основных идей в статистике является понятие функции плотности распределения (плотности вероятности) . В связи с этим важной является проблема ее оценки. Для этого широко используется гистограмма. При ее построении необходимо определить число интервалов (групп) , на которые будет разбита выборочная совокупность. Для этого часто применяют формулу Стерджесса:

 ,                                             (1)

где  — объем выборки. Результат округляют до ближайшего целого числа.

При получении этого результата полагается, что число элементов выборки в -й группе равно биномиальному коэффициенту

.

Сумма коэффициентов (групповых частот) равна

,

она должна совпадать с объемом выборки , следовательно,

.

Логарифмируя последнее выражение, получим формулу Стерджесса, которая статистически необоснованна, но широко распространена в учебной литературе.

Ниже рассмотрим статистические критерии, применяемые для оценки числа интервалов гистограммы или их длины. Используемые формулы являются асимптотическими, т.е. их следует применять при больших объемах выборочных совокупностей.

Минимизации интегральной среднеквадратической ошибки

Обозначим через  оценку истинной функции ,

Еще в работе [1, с. 189] Н.В. Смирнов показал, что уклонение гистограммы от неизвестного графика плотности убывает, как . В работе [3, с. 605] Д. Скотт для оценки длины интервала гистограммы минимизировал интегральную среднеквадратическую ошибку

 ,

где  — точечная дисперсия,  — точечное смещение,  — символ математического ожидания.

Была получена следующая оценка [3, с. 607]

,

где  — длина группового интервала.

Таким образом,

 при .

Минимизируя два первых слагаемых, Скотт получил асимптотическую оценку оптимальной длины интервала [3, с. 607]

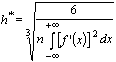.                                                      (2)

Таким образом, в отличие от формулы Стерджесса число интервалов будет пропорционально , а не .

Например, для нормального распределения получим

,                                           (3)

где стандартное отклонение. Формулу (3) часто применяют для первоначальной оценки длины интервалов независимо от вида распределения.

Пусть истинная функция плотности распределения имеет вид (линейное распределение):

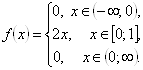                                              (4)

В данном случае

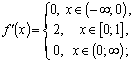
Тогда оптимальная длина интервала будет равна

.

Для числа интервалов получим

.                                                  (5)

Применение информационного критерия Акаике (AIC)

Для оценки оптимального числа интервалов критерий Акаике [2] применяется редко. При этом обычно упоминается работа Тейлора [4]. AIC для оценки оптимального числа интервалов гистограммы  примет вид

.                               (6)

Здесь  — функция правдоподобия. Использование коэффициента 2 в формуле (6) является общепринятым (так сложилось исторически). Функция правдоподобия для гистограммы имеет вид

,

где  — количество выборочных значений переменной в й группе;

 — длина  го интервала гистограммы. При определении функции правдоподобия полагаем, что не должно быть пустых групп и групповых интервалов, равных нулю.

В случае равных интервалов, имеем:

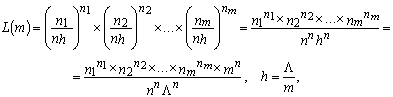
где  — размах вариации.

Натуральный логарифм функции правдоподобия равен:

                                   (7)

где  — слагаемые независящие от числа групп.

Не принимая в расчет величины, независящие от числа групп , подставим (7) в (6), поменяем знак и разделим на 2. Получим, что в случае равных интервалов, оптимальное число групп  равно:

                                              (8)

Рассмотрим равновероятные (равночастотные) интервалы. В этом случае

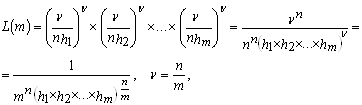
где — длины

Логарифмируя, получим

Тогда, согласно критерию Акаике, оптимальное число интервалов  равно:

                             (9)

Соотношения (8), (9) не содержат предположений о виде функции распределения вероятностей, поэтому являются непараметрическими.

Представляет интерес изучить характер зависимости числа групп  от объема выборки  для различных методов. Поэтому целесообразно получить явные формулы , соответствующие критериям (8), (9).

Пусть функция плотности распределения имеет вид (4). Рассмотрим случай равных интервалов. Разделим отрезок  на  частей и вычислим вероятность того, что значение признака окажется в ом интервале:

.

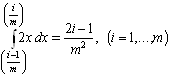Следовательно, число наблюдений в  ом интервале оценим как . В этом случае

Тогда при заданном количестве данных  оптимальное число групп находится из условия

            (10)

Проанализируем выражение (10):

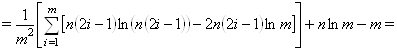
При упрощениях учли, что . Отбросим слагаемое , которое не зависит от числа групп. Введем обозначение

Тогда оптимальное число групп при заданном объеме выборки  соответствует максимуму выражения

                                                   (11)

Дифференцируя (11) по  получим, что при заданном объеме выборки  оптимальное число групп находится из уравнения

                                              (12)

Оценим сумму

.

Согласно формуле Эйлера-Маклорена

где коэффициент Бернулли .

Следовательно

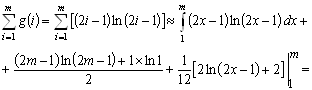
Тогда

Дифференцируя и упрощая, получим

.                    (13)

Согласно (12, 13) оптимальное число интервалов  гистограммы находится из уравнения

                                 (14)

В таблице 1 приведены результаты оценки  для функции плотности вероятности (4) по формулам Стерджесса, Скотта и (14).

Таблица 1.

Число интервалов гистограммы для линейной функции плотности вероятности

Таким образом, при больших  формула Скотта и информационный критерий рекомендуют значительно большее число интервалов по сравнению с формулой Стерджесса.

Список литературы:

1.Смирнов Н.В. О построении доверительной области для плотности распределения случайной величины // Доклады АН СССР. — 1950. — Т. 74. — № 2. — С. 189—192.

2.Akaike H. Information theory as an extension of the maximum likelihood principle. In B. N. Petrov & F. Csaki (Eds.). Second International Symposium on Information Theory. — Budapest: Akademiai Kiado, 1973. — P. 267—281.

3.Scott D.W. On optimal and data-based histograms // Biometrika. — 1979. — Vol. 66. — P. 605—610.

4.Taylor C. Akaike's information criterion and the histogram // Biometrika. — 1987. — Vol. 74. — P. 636—639.