Статья опубликована в рамках: VI Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 25 сентября 2012 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
НЕКООПЕРАТИВНАЯ ДИФФЕРЕНЦИАЛЬНАЯ ИГРА НЭША ДЛЯ ЛИНЕЙНОЙ СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Копец Мирослав Михайлович
канд. физ.-мат. наук, доцент НТУУ «КПИ», г. Киев
Е-mail: miroslav1941@windowslive.com
1. Введение
Некооперативной дифференциальной игрой называют математическую модель, в которой действующие стороны (игроки) до начала процесса игры не могут договариваться об используемых ими стратегиях. Другими словами, это означает, что игроки не имеют права создавать коалиции или координировать свои действия. Такие игры называют играми с ненулевой суммой. Обычно в формулировке некооперативной дифференциальной игры двух участников с ненулевой суммой присутствуют уравнение, описывающее динамику процесса, и соответствующие игрокам два функционала, определяющие выигрыши обеих игроков. Для систем со сосредоточенными параметрами такие задачи можно найти в [1, с. 421—423], [4 5]. Игровые задачи для систем с распределенными параметрами рассмотрены, например в [3].
2. Постановка задачи
Пусть объект управления описывается следующей системой линейных уравнений с частными производными
![]() , (1)
, (1)
где ![]() ,
, ![]() — заданные матрицы размера
— заданные матрицы размера ![]() ;
; ![]() ,
, ![]() — заданные матрицы размеров
— заданные матрицы размеров ![]() и
и ![]() соответственно, причем все эти четыре матрицы — постоянные (их элементами являются действительные числа) . Переменная
соответственно, причем все эти четыре матрицы — постоянные (их элементами являются действительные числа) . Переменная ![]() ,
, ![]() ассоциируется со временем, переменная
ассоциируется со временем, переменная ![]() ,
, ![]() , является пространственной переменной,
, является пространственной переменной, ![]() ,
, ![]() и
и ![]() - заданные действительные числа,
- заданные действительные числа, ![]() — действительный
— действительный ![]() -мерный вектор-столбец, в дальнейшем называемый состоянием системы (3), действительные
-мерный вектор-столбец, в дальнейшем называемый состоянием системы (3), действительные ![]() — мерный вектор — столбец
— мерный вектор — столбец ![]() и
и ![]() -мерный вектор-столбец
-мерный вектор-столбец ![]() называются управлениями(стратегиями). Предполагается, что управления принадлежат классу кусочно-непрерывных вектор-функций. Для системы (1) задано начальное условие
называются управлениями(стратегиями). Предполагается, что управления принадлежат классу кусочно-непрерывных вектор-функций. Для системы (1) задано начальное условие
![]() (2)
(2)
и граничное условие
![]() , (3)
, (3)
где ![]() -мерные вектор-столбцы
-мерные вектор-столбцы ![]() и
и ![]() заданы. Рассмотрим следующие критерии оптимальности
заданы. Рассмотрим следующие критерии оптимальности
 , (4)
, (4)
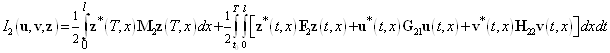 , (5)
, (5)
где выражение ![]() означает скалярное произведение векторов
означает скалярное произведение векторов ![]() и
и ![]() , то-есть
, то-есть ![]() ,
, ![]() и
и ![]() - заданные симметричные положительно определенные матрицы размеров
- заданные симметричные положительно определенные матрицы размеров ![]() и
и ![]() соответственно (следовательно, существуют матрицы
соответственно (следовательно, существуют матрицы ![]() и
и ![]() ),
), ![]() ,
, ![]() ,
, ![]() ,
, ![]() — заданные симметричные неотрицательно определенные матрицы размера
— заданные симметричные неотрицательно определенные матрицы размера ![]() ,
, ![]() и
и ![]() — заданные симметричные неотрицательно определенные матрицы размеров
— заданные симметричные неотрицательно определенные матрицы размеров ![]() и
и ![]() соответственно. Некооперативное равновесие по Нэшу — это пара таких стратегий
соответственно. Некооперативное равновесие по Нэшу — это пара таких стратегий ![]() и
и ![]() , что ни один из игроков не меняет свою стратегию при заданной стратегии другого игрока. В результате имеют место следующие неравенства
, что ни один из игроков не меняет свою стратегию при заданной стратегии другого игрока. В результате имеют место следующие неравенства
![]() для всех возможных управлений
для всех возможных управлений ![]() ;
;
![]() для всех возможных управлений
для всех возможных управлений ![]() .
.
Последние соотношения позволяют применить метод множителей Лагранжа для нахождения оптимальных стратегий [2, с. 31].
3. Преобразование уравнения состояния и функционалов
Оптимальные управления ![]() и
и ![]() будем искать в следующем виде
будем искать в следующем виде
![]() ,
, ![]() , (6)
, (6)
где ![]() и
и ![]() - матричнозначные симметрические функции, подлежащие определению. Подставляя выражения (6) в уравнение (1), имеем
- матричнозначные симметрические функции, подлежащие определению. Подставляя выражения (6) в уравнение (1), имеем
![]() . (7)
. (7)
Дальше из соотношений (6) находим
![]() ,
, ![]() . (8)
. (8)
Используя равенства (6) и (8), получим
![]()
![]() , (9)
, (9)
![]()
![]() . (10)
. (10)
С помощью соотношений (9) и (10) функционалы (4) и (5) преобразуем так
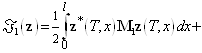
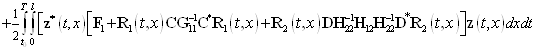 , (11)
, (11)

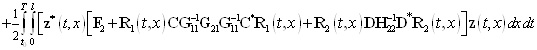 . (12)
. (12)
Таким способом управления ![]() и
и ![]() исключены из уравнения (1), а также из функционалов (4) и (5).
исключены из уравнения (1), а также из функционалов (4) и (5).
4. Уравнения Эйлера-Лагранжа для функционала (4)
Вместо функционала (11) рассмотрим следующий функционал
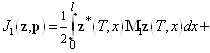
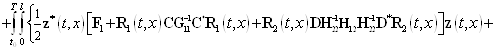
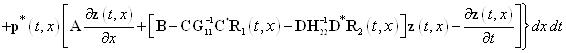 , (13)
, (13)
где ![]() —- неизвестная вектор-функция. Она именуется множителем Лагранжа. Если выполняется равенство (7), то значения функционалов (11) и (13) равны. Дальше найдем приращение
—- неизвестная вектор-функция. Она именуется множителем Лагранжа. Если выполняется равенство (7), то значения функционалов (11) и (13) равны. Дальше найдем приращение ![]() функционала (13). Имеем
функционала (13). Имеем
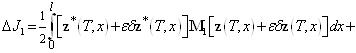
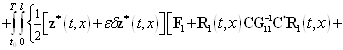
![]()
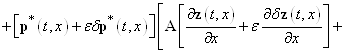
![]()

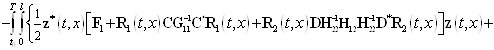

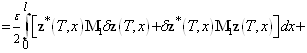
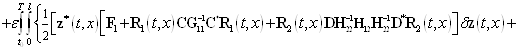
![]()
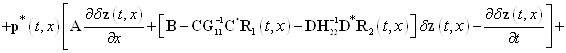
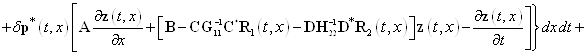
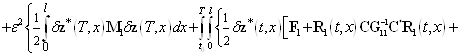

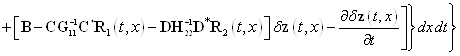 . (14)
. (14)
Имеем ![]() ,
,![]() . Полагаем также, что
. Полагаем также, что ![]() и
и ![]() . Очевидно, справедливы следующие соотношения
. Очевидно, справедливы следующие соотношения
![]() , (15)
, (15)
![]()
![]()
![]() , (16)
, (16)
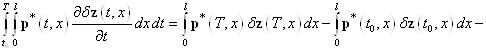
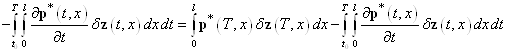 , (17)
, (17)
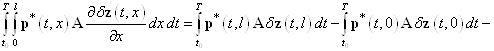
 , (18)
, (18)
![]() . (19)
. (19)
С учетом соотношений (15) — (19) равенство (14) примет вид
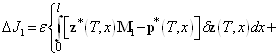
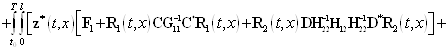
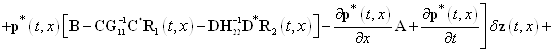
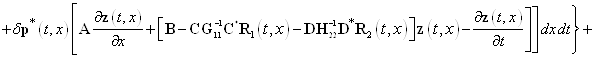
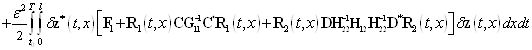 . (20)
. (20)
Равенство нулю первой вариации функционала (13) — это необходимое условие его экстремума. Оно будет выполнено, если коэффициенты при ![]() ,
, ![]() и
и ![]() одновременно равны нулю. Поэтому из соотношения (20) имеем следующие равенства
одновременно равны нулю. Поэтому из соотношения (20) имеем следующие равенства
![]() , (21)
, (21)
![]()
![]() , (22)
, (22)
![]() . (23)
. (23)
Поскольку раньше было сделано предположение, что ![]() и
и ![]() , то окончательно система уравнений Эйлера-Лагранжа для функционала (11) выглядит так
, то окончательно система уравнений Эйлера-Лагранжа для функционала (11) выглядит так
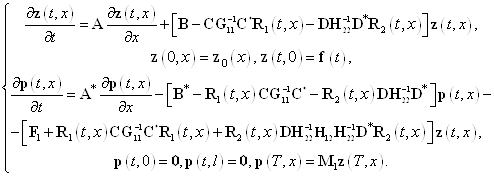 . (24)
. (24)
5. Уравнения Эйлера-Лагранжа для функционала (5)
Аналогично вместо функционала (12) рассмотрим следующий функционал
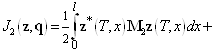
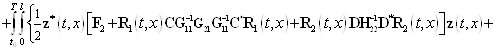
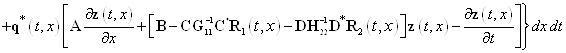 , (25)
, (25)
где ![]() — также множитель Лагранжа. Если выполняется равенство (7), то значения функционалов (12) и (25) равны. Для нахождения приращения
— также множитель Лагранжа. Если выполняется равенство (7), то значения функционалов (12) и (25) равны. Для нахождения приращения ![]() функционала (25) имеем такое выражение
функционала (25) имеем такое выражение
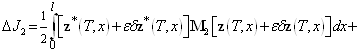
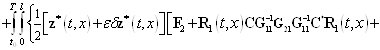
![]()
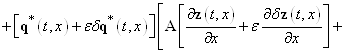
![]()
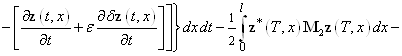
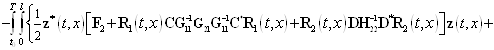

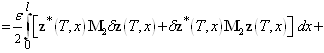

![]()
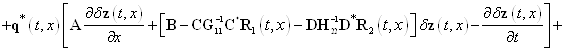
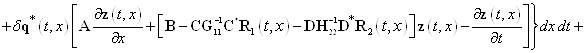
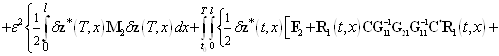
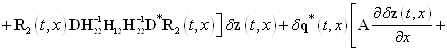
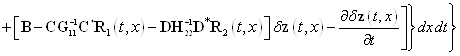 . (26)
. (26)
Снова вспоминаем, что ![]() ,
,![]() , и полагаем также, что
, и полагаем также, что ![]() и
и ![]() . Тогда справедливы следующие соотношения
. Тогда справедливы следующие соотношения
![]() , (27)
, (27)
![]()
![]()
![]() , (28)
, (28)
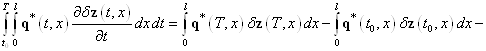
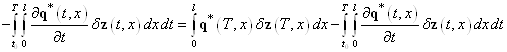 , (29)
, (29)
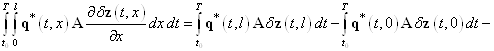
 , (30)
, (30)
![]() . (31)
. (31)
С учетом соотношений (27) — (31) выражение (26) примет вид
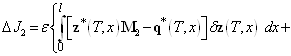

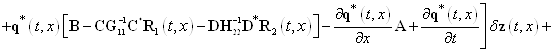
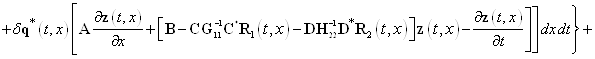
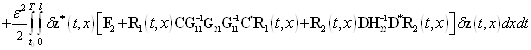 . (32)
. (32)
Равенство нулю первой вариации функционала (25) - необходимое условие его экстремума. Оно будет выполнено, если коэффициенты при ![]() ,
, ![]() и
и ![]() одновременно равны нулю. Поэтому из соотношения (32) имеем такие равенства
одновременно равны нулю. Поэтому из соотношения (32) имеем такие равенства
![]() , (33)
, (33)
![]()
![]() , (34)
, (34)
![]() . (35)
. (35)
Поскольку раньше было сделано предположение, что ![]() и
и ![]() , то окончательно система уравнений Эйлера-Лагранжа для функционала (12) выглядит так
, то окончательно система уравнений Эйлера-Лагранжа для функционала (12) выглядит так
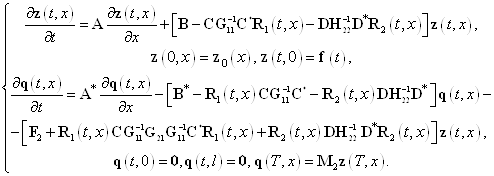 . (36)
. (36)
6. Вывод системы матричных уравнений Риккати с частными производными
На основании равенства ![]() считаем, что существует такая зависимость
считаем, что существует такая зависимость
![]() . (37)
. (37)
Из (37) непосредственно находим
![]() . (38)
. (38)
Если теперь принять во внимание первое уравнение системы (24), то из (38) имеем
![]()
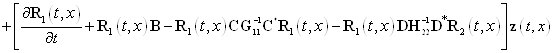 . (39)
. (39)
Дальше используя уравнение для ![]() из системы (24) и очевидное равенство
из системы (24) и очевидное равенство ![]() , получим
, получим
![]()
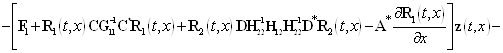
![]() . (40)
. (40)
Сопоставляя равенства (39) и (40), приходим к следующим соотношениям
![]()
![]() , (41)
, (41)
![]() . (42)
. (42)
При этом необходимо также учесть следующие дополнительные условия
![]() ,
, ![]() ,
, ![]() , (43)
, (43)
которые соответственно являются следствиями равенств ![]() ,
, ![]() и
и ![]() . Аналогично, исходя из соотношения
. Аналогично, исходя из соотношения![]() , для функции
, для функции ![]() получим такие уравнения
получим такие уравнения
![]()
![]() . (44)
. (44)
![]() . (45)
. (45)
Функция ![]() удовлетворяет также следующим дополнительным условиям
удовлетворяет также следующим дополнительным условиям
![]() ,
, ![]() ,
, ![]() . (46)
. (46)
Для удобства представим соотношения (41) — (46) в форме одной системы равенств
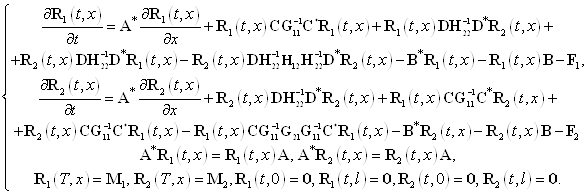 . (47)
. (47)
Подытоживая все вышеизложенное при условии существования оптимальных стратегий ![]() и
и ![]() , можно сформулировать следующие утверждения.
, можно сформулировать следующие утверждения.
Теорема 1. Матричнозначные функции ![]() и
и ![]() удовлетворяют системе соотношений (47).
удовлетворяют системе соотношений (47).
Теорема 2. Оптимальная стратегия ![]() имеет вид
имеет вид ![]() , где функция
, где функция ![]() является решением уравнения (7), удовлетворяет условиям (2) и (3), а матричнозначные функции
является решением уравнения (7), удовлетворяет условиям (2) и (3), а матричнозначные функции ![]() и
и ![]() определяются из системы (47).
определяются из системы (47).
Теорема 3. Оптимальная стратегия ![]() имеет вид
имеет вид ![]() , где функция
, где функция![]() , матричнозначные функции
, матричнозначные функции ![]() и
и ![]() такие же, как и в теореме 2.
такие же, как и в теореме 2.
7. Вычисление минимальных значений функционалов (4) и (5)
Функционал (4) можно преобразовать следующим образом. Имеет место такое равенство
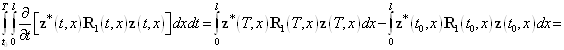
![]() .
.
Отсюда непосредственно находим
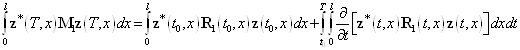 .
.
Это означает, что функционал (4) будет иметь следующий вид
![]()
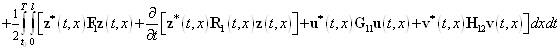 . (48)
. (48)
Поскольку имеет место равенство
![]() ,
,
то функционал (48) можно переписать так
![]()
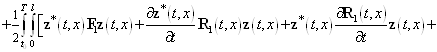
![]() . (49)
. (49)
Из равенства ![]() имеем
имеем ![]() . Дальше получим
. Дальше получим
![]()
![]() ,
,
![]()
![]() .
.
Принимая во внимание эти соотношения и равенство (9), функционал (49) будет иметь следующий вид
![]()
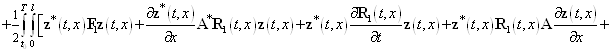
![]()
![]()
![]() . (50)
. (50)
Дальше используем формулу для нахождения производной произведения трех сомножителей
![]()
![]() .
.
Поскольку выполняется соотношение ![]() и согласно формуле Ньютона-Лейбница справедливо равенство
и согласно формуле Ньютона-Лейбница справедливо равенство
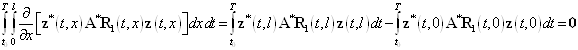 ,
,
то имеет место следующее равенство
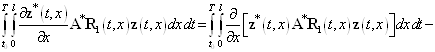
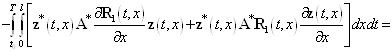
 .
.
Тогда выражение (50) можно преобразовать так
![]()
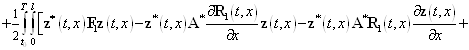
![]()
![]()
![]()
![]() . (51)
. (51)
После группирования в (51) получим
![]()
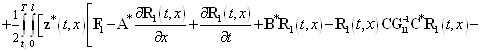
![]()
![]()
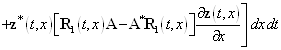 .
.
Если теперь принять во внимание систему уравнений (47), то окончательно получим
![]() . (52)
. (52)
Таким образом, справедливо следующее утверждение.
Теорема 4. Минимальное значение функционала (4) можно вычислить по формуле (52), где матричнозначная функция ![]() является решением системы уравнений (47), а функция
является решением системы уравнений (47), а функция ![]() удовлетворяет уравнению (7) и дополнительным условиям (2) — (3).
удовлетворяет уравнению (7) и дополнительным условиям (2) — (3).
Аналогично можно получить следующее соотношение
![]() . (53)
. (53)
Теорема 5. Минимальное значение функционала (5) можно вычислить по формуле (53), где матричнозначная функция ![]() удовлетворяет системе уравнений (47), а функция
удовлетворяет системе уравнений (47), а функция ![]() такая же, как и в теореме 4.
такая же, как и в теореме 4.
Список литературы:
1.Интрилигатор М. Математические методы оптимизации и экономическая теория. — М.: Айрис-пресс, 2002. — 576 с.
2.Сиразетдинов Т.К. Оптимизация систем с распределенными параметрами. — М.: Наука, 1977. — 480 с.
3.Aihara S.I., Bagchi A. Linear-quadratic stochastic differential games for distributed parameter systems. // Comput. Math. Appl., Vol. 13, No 1—3, pp. 247—259, 1987.
4.Basar T., Olsder G.J. Dynamic Noncooperative Game Theory. Academic Press, London — New York, 1982. — 430 p.
5.Starr A.W., Ho Y.C. Nonzero-sum differential games. // J. Opt. Theory and Appl., Vol. 3, No 3, pp. 184—206, 1969.
дипломов

Оставить комментарий