О классе дискретных функций, принимающих на каждой последовательности значение, равное одному из ее членов

Поляков Николай Львович

Cт. преподаватель кафедры «Математика»,

Финансовый Университет при правительстве РФ, г. Москва

E-mail:

Введение. В данной работе для каждого конечного множества  изучается множество всех функций  на множестве  от любого конечного количества переменных , удовлетворяющих условию

Такие множества естественным образом возникают в теории принятия решений (decision theory) при применении предложенного С. Шелахом в [11] клонового подхода к кругу вопросов, связанных с известной теоремой («парадоксом») К. Эрроу (о теореме Эрроу см. [6], [7], [10], [12]). Математический контекст этих вопросов состоит в следующем. Пусть даны непустые конечные множества «участников голосования»  и «альтернатив» . «Индивидуальной системой предпочтений» каждого участника называется некоторая -функция выбора на множестве А, где  есть некоторое положительное натуральное число, не превосходящее , а под -функцией выбора понимается произвольная функция  из множества  всех -элементных подмножеств множества  в множество , которая удовлетворяет условию  для каждого множества  из своей области определения. Профилем (или -профилем) участников называется произвольная функция  из множества  в множество  всех -функций выбора на множестве . Правилом голосования (или -правило голосования) называется функция, которая каждому -профилю  ставит в соответствие некоторую -функцию выбора  на множестве . Последняя называется «коллективной системой предпочтений». Правило голосования называется простым, существует такая функция , что для каждого профиля  и множества  имеет место равенство

Будем в этом случае говорить, что функция  определяет -правило голосования (2). Легко заметить, что функции с условием (1) и только они определяют -правила голосования (2) для каждого натурального числа . Функции, удовлетворяющие условию (1), будем называть функциями голосования, а множество всех функций голосования (от любого числа переменных) на произвольном множестве , будем обозначать символом  или просто , если контекст не допускает двусмысленности.

Основные определения и обозначения. Элементы декартовой степени , , произвольного множества  будем отождествлять с последовательностями , , , т.е. с функциями ; поэтому для любой последовательности  мы употребляем стандартные обозначения  и  соответственно для ее области определения и области значений. Будем использовать обозначение  для множества .

Для каждого натурального числа  множество всех -местных функций на множестве , т.е. всех функций , будем обозначать символом , и положим . Если контекст не допускает разночтений вместо  и  будем писать просто  и . Для краткости для любого множества  вместо  будем писать .

Функция от  переменных, которая ставит в соответствие каждой последовательности  элемент  для некоторого фиксированного номера , называется -местной -ой проекцией или селекторной функцией. Мы будем обозначать такие функции символами  или просто , если арность проекции восстанавливается из контекста.

Клоном на множестве  называется любое (функционально) замкнутое подмножество множества , которое содержит все проекции (о клонах и функционально замкнутых множествах см., например, [2], [4], [5] или [9]). Подчеркнем, что каждое функционально замкнутое множество вместе с каждой функцией  содержит все функции, которые отличаются от нее только несущественными переменными.

В литературе можно найти другие определения понятия клон. В [1] клоном  называется любое подмножество множества , которое содержит все проекции, и для всех натуральных  вместе с каждой функцией  и функциями ,,..., содержит функцию

Легко проверить, что если дополнительно потребовать, чтобы множество  вместе с каждой функцией  содержало бы все функции, которые отличаются от функции  только несущественными переменными, то получим определение, эквивалентное данному выше. В настоящей работе мы будем использовать эквивалентность этих определений; функцию  мы будем просто обозначать посредством знакосочетания .

Подклоном клона  называется любое подмножество множества , которое является клоном. Ограничением  клона  на множестве  на множество , назовем множество . Множество  называется носителем клона . Множество , для которого ограничение  является клоном (т.е. содержит только функции из ) назовем подносителем клона  и множество всех подносителей клона  обозначим символом . Минимальный по включению клон  на множестве , содержащий все функции из некоторого множества  называется порожденным множеством  (или функциями из ). Изоморфизмом  клонов  и  на множествах  и  соответственно будем называть такую биекцию , что алгебраические структуры  и  являются моделями некоторой сигнатуры , и  есть изоморфизм этих структур. Клоны на двухэлементных множествах (каждый из которых изоморфен некоторому постовскому классу) мы будем называть бинарными. Постовскую классификацию и элементарные свойства бинарных функций (см. [3], [8]) мы будем использовать без специальных ссылок.

Клон функций голосования на конечном множестве. Легко проверить, что множество  всех функций голосования на любом множестве  замкнуто относительно постовских операций и содержит все селекторные функции, т.е. является клоном. Каждый поклон множества  будем называть клоном голосования. Если множество  есть , то клон  в точности является постовским классом  булевых функций, сохраняющих  и . Этот класс порождается множеством функций  и содержит счетное число неизоморфных подклассов. Таким образом, каждый бинарный клон голосования изоморфен некоторому подклассу класса . Множество всех таких подклассов, описанное Постом, среди прочего, в [8], обозначим символом .

Для любого множества  ограничение  клона голосования  на множестве  на множество  является клоном голосования на множестве (т. е. ). Для каждого клона голосования  на множестве  его бинарным следом  будем называть такую функцию из множества  всех двухэлементных подмножеств множества  в множество , что клоны  и  изоморфны. Для определенности будем считать, что в множестве  зафиксировано некоторое максимальное по включению подмножество  попарно неизоморфных классов, и значение функции  принадлежит  для всех клонов голосования  и двухэлементных множеств . Легко проверить, что в этом случае постовский класс  однозначно определяет клон . Для каждого двухэлементного множества  и постовского класса  обозначим изоморфный ему клон с носителем  символом .

 Пусть  – некоторое подмножество множества  всех подмножеств множества , и для каждого  определен клон голосования  на множестве , причем для всех множеств

Тогда множество всех функций , таких, что для любого множества  ограничение  принадлежит клону , является клоном голосования на множестве . Такой клон мы будем называть свободной склейкой семейства клонов . Заметим, что если семейство  состоит из не более чем двухэлементных множеств, условие  выполняется автоматически, что доказывает следующее

Предложение. Для любого множества , , и функции  определена свободная склейка  семейства клонов . Для любого клона голосования  имеет место включение .

Оказывается, для любого множества , , множество всех свободных склеек семейств  допускает несложное описание. Следующее условие для клона  на множестве  будем обозначать 

: для любых последовательностей  с различными областями значений и элементов  и  существует такая функция , что , .

Теорема 1. Пусть дано конечное множество  мощности . Тогда любой клон голосования  на множестве  удовлетворяет условию  тогда и только тогда, когда он является свободной склейкой некоторого семейства бинарных клонов .

Доказательство. В сторону «только тогда» теорема очевидна. Будем доказывать теорему в другую сторону. Для каждого натурального числа  функцию  будем называть допустимой на множестве , если для каждого множества  существует такая функция , что ограничения функций  и  на множество  совпадают.

Индукцией по мощности множества  докажем, что для любой допустимой на множестве  функции  клон  содержит такую функцию , что  (из чего теорема немедленно следует в другую сторону).

Если , в качестве функции  можно взять некоторую селекторную функцию. Пусть , и утверждение доказано для всех множеств  меньшей мощности. Выберем произвольную допустимую на множестве  функцию . Очевидно, она допустима и на любом подмножестве множества . Для любой последовательности  и любого элемента  обозначим символом  некоторую фиксированную функцию из множества  в множество , которая принимает значение  на последовательности  и совпадает с функцией  на множестве . Предположим, что существует функция , которая не допустима на множестве . Тогда  и существует такое множество , что  и любая функция , которая совпадает с функцией  (а, следовательно, с функцией ) на множестве , принимает на последовательности  значение, отличное от , т. е. . По предположению индукции клон  содержит функцию, которая совпадает с функцией  (и функцией ) на множестве . Следовательно, эта функция совпадает с функцией  и на множестве , что доказывает шаг индукции в этом случае.

Пусть теперь любая функция  допустима на множестве  и, следовательно, для каждой последовательности  по предположению индукции клон  содержит функцию , которая совпадает с функцией  на множестве . Зафиксируем некоторое семейство  и построим функцию  с требуемыми свойствами.

Если для некоторой пары  различных последовательностей из  существует такая функция  из зафиксированного семейства, что , то можно положить . Предположим, что таких функций не существует. Заметим, что для всякой функции  функция  совпадает с функцией  на множестве  (это следует из того, что каждая функция , очевидно, удовлетворяет условию ).

Случай 1: существуют такие последовательности , что для некоторых элементов  имеют место равенства и неравенство

Тогда можно положить , где функция  такова, что:

                                      .

Случай 2: существуют такие последовательности , что для некоторых элементов  имеют место равенства и включение

Тогда можно положить , где функции  таковы, что

Случай 3: случаи 1-2 не выполнены. Из невыполненности случая 2 следует, что  для любых последовательностей . Обозначим множество , , символом .

Подслучай 3.1: . Противоречит допустимости функции .

Подслучай 3.2:  и существуют такие элементы , что  для некоторого элемента . Из невыполненности случая 1 следует, что  для некоторого элемента . Выберем элемент , и пусть .

Тогда можно положить , где функции  таковы, что                                                                

Подслучай 3.3: , и  для всех элементов . Если множество  состоит ровно из двух различных последовательностей  и , существует такая селекторная функция , что . Пусть , , , . Из невыполненности случая 1 следует, что для любых функций  и  имеют место равенства  и . Тогда можно положить , где функции  таковы, что

Пусть теперь . Выберем различные последовательности  и элементы , для которых

Как было отмечено в начале доказательства, функции  и  допустимы на множестве . Согласно подслучаю 3.2 существуют функции , которые на множестве  соответственно совпадают с функциями  и . Тогда можно положить , где функция  такова, что

Теорема доказана.

Следствие 1. Для любого конечного множества  клон  порождается функциями от не более чем трех переменных, причем функцию от трех переменных достаточно взять одну.

Доказательство. Легко проверить, что клон  есть свободная склейка такого семейства бинарных клонов , что  для всех множеств  Для каждого двухэлементного множества  зафиксируем некоторую биекцию . Рассмотрим клон , порожденный всеми функциями голосования от двух переменных и любой трехместной функцией , которая на любой последовательности  принимает значение , где  и . Заметим, что среди функций голосования от двух переменных содержится некоторая функция , которая на любой последовательности  равна , где , а символом  обозначена бинарная конъюнкция. Поскольку множество  порождает класс , для каждого двухэлементного множества  клон  содержит все функции голосования на . Кроме того, клон , очевидно, удовлетворяет условию . Поэтому по теореме 1 он совпадает с множеством . Следствие доказано.

Заметим, что, очевидно, функций только от двух переменных недостаточно для порождения всего множества  уже при .

Для каждого действительного числа  символом  обозначается наименьшее натуральное число, большее или равное .

Следствие 2. Для любого конечного множества  множество  порождается одной функцией от не более чем  переменных.

Доказательство. Зафиксируем опять некоторую биекцию  для каждого двухэлементного множества . Легко проверить, что существует множество функций  мощности не более , которое содержит определенную в доказательстве следствия  функцию 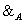 и для любых двух последовательностей  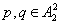с несовпадающими областями значения содержит функцию 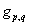, для которой либо , либо . Положим  и поставим в инъективное соответствие каждой функции  некоторую последовательность , не равную тождественно нулю или единице. Рассмотрим такую функцию , что  для всех функций , а  совпадает с определенной в доказательстве следствия 1 функцией . Пусть  – клон, порожденный функцией . Очевидно, любое его ограничение , , изоморфно постовскому классу . Кроме того, можно заметить, что клон  содержит трехместную функцию , которая на любой последовательности  принимает значение , где , а символ  означает сложение по модулю два. Покажем, что клон  удовлетворяет условию . Достаточно показать, что для каждого натурального числа  клон  содержит функцию f, для которой . Но для одного из номеров  такой функцией  является функция , а для другого функция . Теперь по теореме  получаем равенство . Следствие доказано.

Список литературы:

1.Кон П. Универсальная алгебра. – М.: МИР, 1968. – 352 с.

2.Мальцев А.И. Итеративные алгебры и многообразия Поста // Алгебра и логика. Семинар 5-1966. – Т. 5, вып. 2. – С. 5—24.

3.Марченков С.С. Замкнутые классы булевых функций. – М.: Физматлит, 2000. – 128 с.

4.Марченков С.С. Функциональные системы с операцией суперпозиции. – М.: Физматлит, 2004. – 104 c.

5.Яблонский С.В. Функциональные построения в k-значной логике. Сборник статей по математической логике и ее приложениям к некоторым вопросам кибернетики // Тр. МИАН СССР, вып. 51. – 1958. – C. 5–142.

6.Arrow, K. A Difficulty in the Concept of Social Welfare // Journal of Political Economy. № 58. 1950. P. 328—346

7.Fishburn P. The Theory of Social Choice. Princeton University Press, 1973.

8.Post, E.L., The Two-Valued Iterative Systems of Mathematical Logic. – Princeton University Press, 1941.

9.Rosenberg I.G. La structure des fonctions de plusieurs variables sur un ensemble fini // C.R. Acad. Sci. Paris. Ser. A.B. 1965. V. 260. P. 3817—3819.

10. Rubinstein A., Fishburn P. Algebraic aggregation theory/ // J. Econom. Theory. 1986. № 38. P. 63—77.

11.Shelah S. On the Arrow property // Advances in Applied Mathematics. 2005. № 34. P. 217—251.

12.Shelah S. What majority decisions are possible // Discrete Mathematics. 2009. № 309. P. 2349—2364.