Статья опубликована в рамках: III Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 11 июня 2012 г.)
Наука: Математика
Секция: Вычислительная математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Операции над сетями Петри
Маслаков Максим Петрович
соискатель, ассистент СКГМИ (ГТУ), г. Владикавказ
E-mail: kalbash1@mail.ru
Маслаков Денис Петрович
Аспирант, ассистент СКГМИ (ГТУ), г. Владикавказ
E-mail: d-maslakov@mail.ru
Как известно сеть Петри состоит из 4-х элементов: множество позиций Р, множество переходов Т, входная функция I и выходная функция О. Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция О отображает переход tj в множество позиций О(tj), называемых выходными позициями перехода.
Структура сети Петри определяется ее позициями, переходами входной и выходной функции.
Определение:
Сеть Петри С является четверкой С=(Р, Т, I, О), где
Р={р1, p2, ..., pn} – конечное множество позиций, n≥0;
Т={t1, t2, ..., tm} – конечное множество переходов, m≥0. Множество позиций и множество переходов не пересекаются, Р∩Т=Ø;
I: T→P∞ есть входная функция – отображение из переходов в комплекты позиций;
О: T→P∞ есть выходная функция – отображение из переходов в комплекты позиций.
Мощность множества Р есть число n, а мощность множества Т есть число m. Произвольный элемент Р обозначается символом рi, i=1, ..., n, а произвольный элемент Т – символом tj, j=1, ..., m.
Позиция pi является входной позицией перехода tj в том случае, если pi ÎI(tj); pi является выходной позицией, если pi ÎО(tj) [1, с. 101]
Операции над сетями Петри описанные в [3, с. 71]:
1. Конкатенация – последовательная комбинация сетей;
2. Объединение – композиция аналогична объединению множеств;
3. Параллельная композиция – параллельное функционирование сетей;
4. Пересечение – аналогична теоретико-множественному определению пересечения;
В настоящей работе вводится операция, взятия декартова произведения сетей Петри по аналогии с декартовым произведением графов и автоматов, описанная в [2, с. 162].
Для данных сетей Петри С1=(Р1, Т1, I1, О1) и С2=(Р2, Т2, I2, О2) декартовым произведением называется сеть Петри С=(Р, Т, I, О), где позиции и переходы C(P)=P1 x P2 и C(T)=T1 x T2 – декартово произведение множеств позиций и переходов исходных сетей, соответственно. А входная и выходная функции – I и O, далее называемая отношение смежности вершин F=(I,O), равная F=PxTÈTxP – задает множество дуг, соединяющих позиции и переходы, причем множествa {PxT}∩{TxP}=Ø. Дуга f (PxT), соединяющая позицию P(p1p2) с переходом T(t1t2), существует, если существует дуга f1 (p1t1) и дуга f2 (p2t2) в исходных сетях Петри, аналогично, существует дуга f (TxP), соединяющая переход T(t1t2) с позицией P(p1p2), если существует дуга f1 (t1p1) и дуга f2 (t2p2) в исходных сетях Петри.
Пусть заданы две сети Петри C1 (P, T, F1) и C2 (S, Z, F2) (Рис. 1). Необходимо произвести их декартово произведение.
Множество позиции данных сетей Петри Р={P1, P2} и S={S1, S2, S3}
Множество переходов этих сетей Т={t1, t2} и Z={z1, z2}
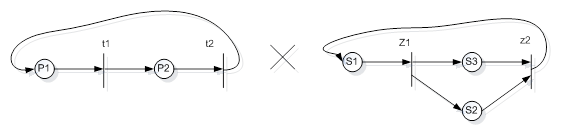
Рисунок 1. Сети Петри C1 (P, T, F1) и C2 (S, Z, F2)
Декартово произведение множеств позиций и переходов:
V=P x S={P1, P2} x {S1, S2, S3}=[V1={P1S1}, V2={P1S2}, V3={P1S3}, V4={P2S1}, V5={P2S2}, V6={P2S3}];
M=T x Z={t1, t2} x {z1, z2}=[m1={t1z1}, m2={t1z2}, m3={t2z1}, m4={t2z2}].
Отображение позиций в переходы, входная функция F(I) равна:
I (m1)=F(t1) x F(z1)={P1} x {S1}={ P1S1}=V1;
I (m2)=F(t1) x F(z2)={P1} x {S2 S3}={ P1S2}, {P1S3}=V2, V3;
I (m3)=F(t2) x F(z1)={P2} x {S1}={ P2S1}=V4;
I (m4)=F(t2) x F(z2)={P2} x {S2 S3}={ P2S2}, {P2S3}=V5, V6;
Отображение переходов в позиции, выходная функция F(O) равна:
O (m1)=F(t1) x F(z1)={P2} x {S2 S3}={ P2S2}, { P2S3}=V5,V6;
O (m2)=F(t1) x F(z2)={P2} x {S1}={ P2S1}=V4;
O (m3)=F(t2) x F(z1)={P1} x {S2 S3}={ P1S2}, { P1S3}=V2,V3;
O (m4)=F(t2) x F(z2)={P1} x {S1}={ P1S1}=V1;
На основании выше проведенных вычислений получаем сеть Петри, являющуюся произведением C1 (P, T, F1)и C2 (S, Z, F2) (Рис. 2).
Также рассмотрено матричное представление декартова произведения сетей Петри.
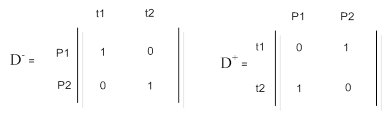
Матрица входной функции сети Петри D- есть матрица строки которой являются позициями сети, а столбцы переходами сети Петри, на пересечении i-ой строки с ј-ым столбцом ставится единица, если i-ая позиция входит в ј-ый переход, ноль в противном случае.
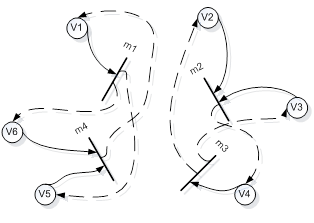
Рисунок 2. Сеть Петри, являющаяся произведением сетей Петри
C1 (P, T, F1) и C2(S, Z, F2)
Матрица выходной функции сети Петри D+ есть матрица строки которой являются переходами сети, а столбцы позициями сети Петри, на пересечении i-ой строки с ј-ым столбцом ставится единица, если i-ый переход входит в ј-ую позицию, ноль в противном случае.
Матрица D- определяет входы в переходы, а D+ - выходы. Матричная форма представления сети Петри С (P, T, D-, D+) эквивалентна стандартной форме представления сетей Петри, но позволяет дать определения сети в терминах векторов и матриц [2, с. 106].
Пусть даны сети Петри C1 (P, T, F1) и C2 (S, Z, F2) (Рис. 3).

Рисунок 3. Сети Петри C1 (P, T, F1) и C2(S, Z, F2)
Произведем декартово произведение представленных сетей.
Множество позиции данных сетей Петри Р={P1, P2} и S={S1, S2, S3}
Множество переходов этих сетей Т={t1, t2} и Z={z1, z2, z3, z4}
Декартово произведение множеств позиций и переходов:
V=P x S={P1, P2} x {S1, S2, S3}=[V1={P1S1}, V2={P1S2}, V3={P1S3}, V4={P2S1}, V5={P2S2}, V6={P2S3}];
M=T x Z={t1, t2} x {z1, z2, z3, z4}=[m1={t1z1}, m2={t1z2}, m3={t1z3}, m4={t1z4}, m5={t2z1}, m6={t2z2}, m7={t2z3}, m8={t2z4}].
Строим матрицы входной и выходной функций, D- и D+ соответственно, для сети Петри C1 (P, T, F1):
Для сети Петри C2 (S, Z, F2):
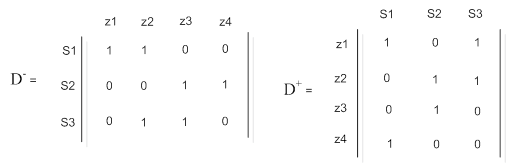
Теперь строим матрицы D- и D+ для C (V, M, F) - произведения двух сетей C1 (P, T, F1)и C2(S, Z, F2). Матрицы входной D- и выходной функций D+ искомой сети Петри C (V, M, F) получились путем перемножения матриц входной и выходной функции D- и D+ сетей Петри C1 (P, T, F1) и C2 (S, Z, F2), соответственно (Рис. 4).
На основании полученных матриц входной D- и выходной D+ функций строим сеть Петри C (V, M, F), являющуюся произведением C1 (P, T, F1) и
C2 (S, Z, F2) (Рис. 5).
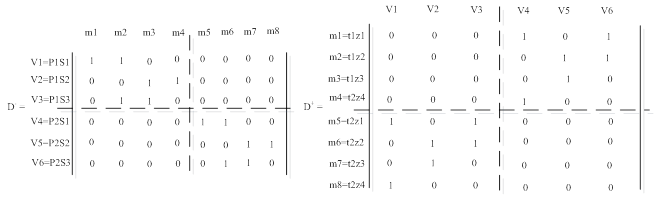 Рисунок 4. Матрицы входной D- и выходной функций D+ искомой сети Петри C (V, M, F)
Рисунок 4. Матрицы входной D- и выходной функций D+ искомой сети Петри C (V, M, F)
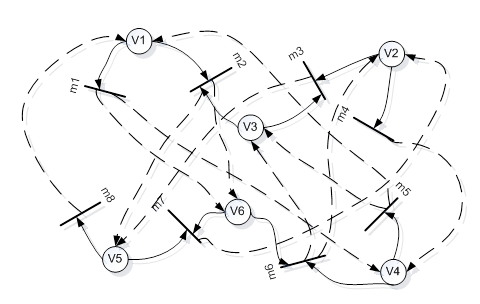
Рисунок 5. Произведение сетей Петри C1 (P, T, F1) и C2(S, Z, F2) (рисунок 3)
Список литературы:
1.Захаров Н.Г., Рогов В.Н. Синтез цифровых автоматов: учеб. пособие. Ульяновск: УлГТУ, 2003. - 135 с.
2.Мелихов А.Н. Ориентированные графы и конечные автоматы: монография. М.: Наука, 1971. – 416 с.
3.Питерсон Дж. Теория сетей Петри и моделирование систем: Пер. с англ. М.: Мир, 1984. - 264 с.
дипломов

Оставить комментарий