О СХОДИМОСТИ РАЗНОСТНОЙ СХЕМЫ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ С НЕЛОКАЛЬНЫМ ИСТОЧНИКОМ

Карданова Муслимат Лиуановна

ассистент кафедры вычислительной математики

КБГУ, г. Нальчик

e-mail: muslimat.kardanova@mail.ru

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (регистрационный номер НИР: 1.6197.2011).

Параболические уравнения с нелинейным нелокальным источником встречаются при описании различных процессов, в которых учитываются эффекты памяти [2].

Цель работы: Получение априорных оценок для решения первой краевой задачи уравнения теплопроводности с нелокальным интегральным источником в дифференциальной и разностной формах.

1.Постановка задачи и априорная оценка. В прямоугольнике

 рассматривается первая краевая задача

 , , (1)

,                                                    (2)

 , ,                                                                (3)

где:  

Умножим уравнение (1) на  и проинтегрируем по переменной  от  до . Тогда получим

Преобразуем с учетом граничных условий слагаемые равенства (4):

где:  .

В силу равенства  имеем

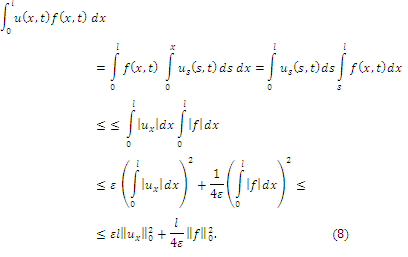
Из равенства (4) с учетом (5)—(8) получаем неравенство:

,

которое при  принимает вид

(9)

Проинтегрируем неравенство (9) по  от  до :

Из априорной оценки (10) следует единственность и непрерывная зависимость решения задачи (1)—(3) от входных данных.

 2.Разностная схема. Введем пространственную сетку  

и сетку по времени  с шагами  и .

Обозначим

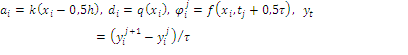
Дифференциальной задаче (1)-(3) поставим в соответствие разностную схему

Разностная схема (11)—(13) имеет порядок аппроксимации , где  при и  при  [3].

Результаты работы.

Теорема. Пусть тогда условия , достаточно для абсолютной устойчивости разностной схемы (11)—(13), и для ее решения справедлива оценка

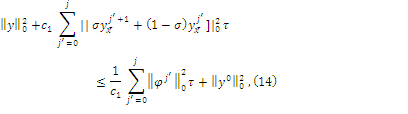
где:   .

Доказательство. Умножим уравнение (11) на  и просуммируем по  от  до . Тогда получим

где .

Преобразуем слагаемые равенства (15):

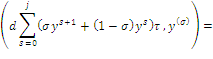
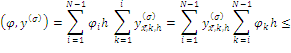
Подставляя (16)—(19) в равенство (15) получим

где: , ,

Из (20) при , следует неравенство

Умножив неравенство (21) на  и просуммировав по  от 0 до , в силу условия  получим априорную оценку (14).

Согласно теореме разностная схема (11)-(13) абсолютно устойчива при  и имеет порядок аппроксимации  при  и порядок при  . Устойчивость и сходимость для случая  требует дальнейшего исследования.

Список литературы:

1. Алиханов А. А., Нелокальные краевые задачи в дифференциальных и разностных трактовках // Дифференциальные уравнения. 2008. Т. 44, № 7. C. 924—931.
2. Кожанов А. И., Параболические уравнения с нелинейным нелокальным источником // Сибирский математический журнал. 1994. Т. 35, № 5. C. 1062—1073.
3. Самарский А. А., Введение в теорию разностных схем. М.: Наука, 1971. 552 с.
4. Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1977. — 735 с.