ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

Бунтова Елена Вячеславовна

доцент, канд.пед. наук, ФГБГУ ВПО СГСХА, г. Самара

Бунтова Оксана Сергеевна

абитуриент, ФГБОУ ВПО СГАУ, г. Самара

E-mail: 

Задачи практики довольно часто приводят к решению основной задачи математической статистики — оценки числовых характеристик на основании экспериментальных данных. При этом возникает вопрос, как посредством соответствующим образом поставленных испытаний, определить, имеют ли место в действительности те условия, на основании которых сделаны априорные оценки.

Во многих учебниках и учебных пособиях по математической статистике [2, 3, 4, 8] представлен материал, который позволяет полу­чить формализованное представление о применении математической статистики к реальному эксперименту.

Для бакалавров, магистров, аспирантов представляет интерес эксперимент — от появления идеи и проблем постановки экспери­мента до получения результатов и обработки данных.

Таким образом, возникла необходимость выделить те вопросы математической статистики, которые позволят обосновать методику оценки погрешностей экспериментальных результатов, выявить особенности обработки ограниченного числа опытов.

Эксперимент — метод изучения явления, объекта, когда исследо­ватель активно и целенаправленно воздействует на него путем создания искусственных условий или использует естественные условия, необходимые для выявления некоторых свойств данного явления или объекта [6].

В эксперименте свойства явлений и объектов изучаются с по­мощью измерений соответствующих величин, например физических. По способу получения результата выделяют прямые (непосредст­венные) и косвенные измерения. При прямых измерениях искомое значение величины определяют соответствующим прибором, то есть происходит непосредственное сравнение с эталоном. Если искомое значение величины находят на основании известной зависимости меж­ду этой величиной и величинами, найденными прямыми измерениями, то этот вид измерений называют косвенным.

Неотъемлемой составляющей любого экспериментального иссле­дования является оценка измерений. Вследствие неточности измери­тельных приборов, несовершенства органов чувств человека, неполноты знаний, трудности учета побочных явлений при повторении одного и того же измерения получаются разные числовые значения измеряемой величины. Кроме того, в основу любого экспериментального исследо­вания, сопряженного с измерениями, заложена модель. Модель содер­жит физическое описание исследуемого объекта или процесса, которое позволяет составить его математическое описание. Неверно построенная модель, в которой не нашли отражения какие-то важные процессы или факторы, влияющие на результат измерений, также приводит к несоответствиям.

При практическом использовании результатов тех или иных измерений возникает вопрос о точности измерений, то есть степени приближения результатов измерения к некоторому действительному значению. Для количественной оценки используется понятие «погрешность измерений» или «ошибка».

Измеряемые в эксперименте величины, вычисляемые по получен­ным из модели рабочим формулам, содержат погрешности, которые носят название модельных погрешностей.

Случайные погрешности при повторных измерениях погреш­ности этого типа показывают свою случайную природу. Возникают они вследствие множества причин, совместное воздействие которых на каждое отдельное измерение невозможно учесть или заранее уста­новить. Единственно возможный способ объективного учета случай­ных погрешностей состоит в определении их статистических законо­мерностей. Рассчитанные статистические оценки вносят в оконча­тельный результат эксперимента.

Исключить случайные ошибки при измерении нельзя, однако применение метода теории ошибок позволяет более точно установить возможную ошибку окончательного результата измерений.

В зависимости от формы представления различают абсолютную, относительную и приведенную погрешности измерений. В зависи­мости от характера проявления, причин возникновения и возможнос­тей устранения различают систематическую и случайную составляющую погрешности измерения, а также грубые погрешности (промахи) [5].

Обычно систематические ошибки и промахи считают устранен­ными и учитывают только случайные ошибки.

Рассмотрим погрешности прямых равноточных измерений на примере измерений в физике, метрологии.

При прямых измерениях числовые значения измеряемой вели­чины  сразу получается из показаний прибора, при помощи которого выполняется измерение. Например, длина стержня при отсчете по шкале линейки.

Результат каждого прямого измерения включает случайную ошибку, которая зависит от большого числа случайных факторов. Если отклонения, вызываемые этими факторами, по абсолютной величине меньше чувствительности прибора, то они не обнаруживаются. В этом случае критерием точности измерения является цена наименьшего деления шкалы прибора или ее половины. Если же отклонения, вызванные случайными факторами, сравнимы по абсолютной величине с чувствительностью прибора, то они обнаруживаются приборами. При  измерениях одной и той же величины получаются результаты , которые могут отличаться друг от друга в пределах чувствительности данных измерений.

Среднее арифметическое из этих результатов

есть величина, наиболее близкая к истинному значению, которую называют средним значением. Следовательно, каждое измерение должно быть повторено несколько раз. В теории погрешностей доказывается, что при увеличении числа  среднее арифметическое стремится к истинному значению измеряемой величины.

Разности между средним значением  измеряемой величины и значениями , полученными при отдельных измерениях называются абсолютными ошибками

и могут быть как положительными, так и отрицательными. Для определения средней абсолютной ошибки результата берут среднее арифметическое абсолютных значений отдельных ошибок, то есть

Отношения

называют относительными ошибками отдельных измерений.

Отношение средней абсолютной ошибки результата к его среднему значению дает среднюю относительную ошибку результата измерений:

Принято относительные ошибки выражать в процентах

Истинное значение измеряемой величины находится в интервале

Если точность прибора такова, что при любом числе измерений получается одно и то же число, лежащее между делениями шкалы, то данный метод оценки погрешности неприменим. В этом случае измерение проводится один раз и записывается в виде  где  искомый результат измерения;  средний результат, равный среднему арифметическому из двух значений, соответствующих соседним делениям шкалы, между которыми заключено остающееся неизвестным истинное значение измеряемой величины;  приборная погрешность, равная половине цены деления шкалы прибора.

Рассмотрим погрешность при косвенных измерениях. Измерения называются косвенными, если уравнение измерения имеет вид:

где  результаты прямых измерений;  физические константы и постоянные приборов;  значения измеряемой величины.

При косвенных измерениях средняя абсолютная ошибка  может быть найдена по правилам дифференцирования

Относительная ошибка находится по формуле  Если учесть, что

Тогда

Выполнив все измерения и вычисления окончательный результат записывают в виде

Следует помнить, что доверительный интервал не является исчер­пывающей характеристикой точности результата. Нужна количест­венная характеристика достоверности интервала, которая покажет на сколько можно быть уверенными в том, что истинное значение изме­ряемой величины окажется в пределах доверительного интервала. Такой характеристикой является доверительная вероятность  где  число измерений.

При определении какой либо величины количество измерений может быть большим или малым.

Оценка точности и правильности при большом числе измерений [1].

Важнейшими характеристиками случайных величин, наиболее часто используемыми на практике, являются среднее значение случайной величины, ее дисперсия, коэффициент вариации.

Предположим, что все измерения величины проделаны одним методом и с одинаковой тщательностью. Такие измерения являются равноточными.

В теории ошибок доказывается, что при выполнении нормального закона (закона распределения Гаусса) при измерениях одинаковой точности среднее арифметическое из результатов, полученных при всех измерениях, является наиболее вероятным и наилучшим значением измеряемой величины

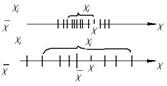
Рис.1 Среднее арифметическое результатов  распределения Гаусса

Распределение результатов измерения относительно среднего значения

Из теории ошибок известно, что плотность распределения случайных ошибок зависит от их величины и выражается формулой:

где:  дисперсия генеральной совокупности, которая характеризует степень разброса вокруг  (Рис.1).

где:  стандартное отклонение, средняя квадратическая ошибка отдельного измерения

Относительная средняя квадратическая ошибка измеряемая в процентах называется коэффициентом вариации:

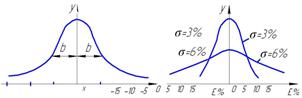
Рис.2 Кривые Гаусса

На рис.2 показаны различные кривые Гаусса. Откуда видно, что максимум плотности распределения случайной ошибки соответствует среднему значению  всех результатов измерений. От этой точки кривая симметрично опускается слева и справа, т.е. положительные и отрицательные ошибки одной величины встречаются одинаково часто. На кривой имеются две точки перегиба, расстояние которых от значения  по оси абсцисс называется стандартным отклонением Стандартное отклонение характеризует воспроизводимость метода измерения. Чем меньше , тем меньше разброс данных и тем более вопроизводим анализ. Рисунок показывает, что каждому значению соответствует своя кривая распределения ошибок. Так для кривой, имеющей ошибки, превышающие 9%, практически не встречаются, а для кривой, соответствующей также ошибки появляются довольно часто. Кривая Гаусса показывает также, что всех результатов имеют величину отклонения от среднего значения

превышающую около 5% результатов больше и около 0,3% результатов больше

Следовательно, при большом числе измерений значение определяет границы достоверности всякого нового определения Можно сказать, что имеется 95% вероятности того, что этот результат окажется в границах

и 99,7% вероятности того, что этот результат окажется в границах:

Это явление получило название «правило 3». Таким образом, средняя квадратичная ошибка определяет доверительный интервал.

Вероятность того, что новое значение измеряемой величины попадает в доверительный интервал, называется доверительной вероятностью, надежностью или коэффициентом надежности.

В лабораторном практикуме обычно задают величину  Это означает, что при большом числе определений результаты каждых 95 определений из 100 будут попадать в доверительный интервал, равный

Для характеристики случайной ошибки необходимо задать два числа: величину самой ошибки (доверительный интервал) и величину доверительной вероятности.

Оценка точности и правильности при малом числе измерений [5].

В лабораторном практикуме имеют дело не с генеральной совокупностью, а с небольшим количеством измерений

Для расчета точности измерений в этом случае пользуются методами математической статистики, разработанной для малого числа измерений. При этом полученные результаты рассматривают как случайную выборку из некоторой генеральной совокупности.

Оценку точности измерений и правильности производят с помощью следующих критериев.

Выборочное среднее — среднее арифметическое.

Единичные отклонения — отклонения отдельных измерений от среднего арифметического (абсолютная ошибка единичного измерения)

Алгебраическая сумма одиночных отклонений равна нулю

Выборочная дисперсия для n найденных значений  случайной величины:

Положительные значения корня квадратичного из дисперсии называется средней квадратической ошибкой отдельного измерения или выборочным отклонением:

Коэффициент вариации:

При оценке точности полученных результатов вычисляют также выборочную дисперсию среднего значения (среднего результата):

Средней квадратической ошибкой среднего арифметического или стандартным отклонением среднего результата:

Доверительный интервал при заданной доверительной вероятности зависит от размера выборки, т.е. от количества проведенных опытов. В общем случае граница доверительного интервала при выбранном коэффициенте надежности выражается уравнением:

где:  коэффициент Стьюдента.

Абсолютная ошибка:

С уменьшением числа измерений n увеличивается доверительный интервал (при той же надежности) или при заданном доверительном интервале уменьшается надежность измерений. По мере увеличения числа измерений величина  стремится к значению  при  и к значению  при

Иными словами, коэффициент Стьюдента  с надежностью  показывает во сколько раз разность между истинным и средним результатами больше стандартного отклонения среднего результата:

Значение  для избранной надежности находят по таблице Стьюдента. Пользуясь формулой для нахождения доверительного интервала и таблицей Стьюдента, можно определить доверительные интервалы по выбранной надежности или, задавшись определенной точностью, рассчитать и по таблице оценить надежность выбранных доверительных интервалов. Кроме того, можно установить число параллельных измерений, необходимых для того, чтобы средний результат имел точность не ниже заданной.

Относительную ошибку среднего результата вычисляют с надежностью  по формуле:

Таким образом, значения полностью определяет точность (воспроизводимость и правильность) измерений.

Рассмотрим применение статистической обработки результатов измерений при изучении законов равноускоренного движения на машине Атвуда [7].

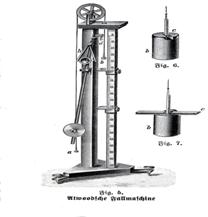
Рис.3 Машина Атвуда

Для равноускоренного движения грузов, проходящих высоту за время  с ускорением в скалярном виде справедливо выражение

Если тело начинает двигаться из состояния покоя, то есть его начальная скорость то вышеприведенное выражение принимает вид:

Выразим из этой формулы ускорение  с которым падает груз:

Эта формула является расчетной формулой и позволяет вычислить ускорение  для известного времени падения грузов с высоты

Результаты измерений и вычислений заносят в таблицу [2].

Таблица 1

Вычисление ускорения при известном времени падения грузов

Окончательный результат представляют в виде

Абсолютная ошибка:

Проведенные вычисления:

Таблица 2

Статистический ряд распределения случайной величины (ускорения)

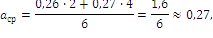
Единичные отклонения

Оценивают точность полученных результатов и вычисляют выборочную дисперсию среднего значения (среднего результата):

Средней квадратической ошибкой среднего арифметического или стандартным отклонением среднего результата:

Граница доверительного интервала при выбранном коэффициенте надежности

где:  коэффициент Стьюдента.

Абсолютная ошибка:

В науке и технике измерения занимают центральное место. Прогресс в этих областях связан с повышением их точности. Из-за неизбежности погрешностей измеренное значение не соответствует в точности истинному значению. Чтобы результат измерения можно было далее использовать, необходимо указывать значения погрешностей измерения.

Список литературы:

1. Бунтова Е. В. Статистическая обработка результатов измерений: учебное пособие. Самара: «Книга», 2011. — 87 с.
2. Бунтова О. С. Статистическая обработка результатов измерений: доклад на 31-й межвузовской студенческой научно-технической конференция ФГБОУ ВПО «Самарский государственный архитектурно-строительный университет», 2012. — 21 с.
3. Вентцель Е. С. Теория случайных процессов и ее инженерные приложения: учебное пособие. М.: Высшая школа, 2007. — 480 с.
4. Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие. М.: Высшая школа, 1977. — 479 с.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник. — М.: ЮНИТИ-ДАНА, 2003. — 543 с.
6. Кравченко Н. С. Методы обработки результатов измерений и оценки погрешности в учебном лабораторном практикуме: учебное пособие. Томск: Из-во Томского политехнического университета, 2011.— 88 с.
7. Князев Б. А. Начало обработки экспериментальных данных: учебное пособие. Новосибирск: НГУ, 1996.– 93 с.
8. Миронова Т. Ф. Физика. Лабораторный практикум: учебное пособие. Кинель: РИЦ СГСХА, 2007.— 130 с.
9. Письменный Д. Конспект лекций по теории вероятностей и математической статистике. — М.: Айрис-пресс, 2004. — 256 с.