ЗАДАЧА СО СМЕЩЕНИЕМ ДЛЯ ОБОБЩЕННОГО УРАВНЕНИЯ ТРИКОМИ В НЕОГРАНИЧЕННОЙ ОБЛАСТИ

Кауфова Амина Амильевна

студентка 2 года обучения в магистратуре

по направлению «Уравнения в частных производных»

КБГУ г. Нальчик.

Е-mail: azamatkaufov96@mail.ru

Кумыкова Светлана Каншубиевна

канд. физ.-мат. наук, доцент кафедры теории функции и функционального анализа,

КБГУ, г. Нальчик.

Цель исследования: доказать единственность и существование решения поставленной задачи.

Результаты исследования:

Рассматривается уравнение

                                        (1)

в области плоскости комплексного переменного где  - полуплоскость , —конечная область полуплоскости , ограниченная характеристиками уравнения (1), выходящими из точек и отрезком прямой ; интервал прямой .

Задача. Найти функцию  со следующими свойствами:

1.причем , ограничены,  при  может обращаться в бесконечность порядка  где

2.  удовлетворяет уравнению (1) в  и краевым условиям

                                                       (2)

                                       (3)

где:

аффиксы точек пересечения характеристик уравнения (1), выходящих из точки  с характеристиками AC и BC соответственно, операторы дробного в смысле Римана — Лиувилля интегро — дифференцирования [4];  - заданные функции, причем

 и могут обращаться в бесконечность порядка не выше  при x=0 и x=1, а при достаточно больших |x| удов­летворяют неравенству  где

Вопросы однозначной разрешимости задачи (1)—(3) в ограниченной и неограниченной областях исследовались в работах Кумыковой С. К. [2] и Денисовой З. Г. [1] при.

Задача (1)—(3) относится к классу задач со смещением А. М. Нахушева [3].

Результатом работы является доказательство теоремы единственности.

Теорема единственности. В области D не может существовать более одного решения задачи (1)— (3), если выполняются условия

где:

Доказательство. Пусть решение задачи, удовлетворяющей однородным граничным условиям

Интегрируя тождество

по области  и учитывая, что , после некоторых преобразований получаем

где:

При выполнении условий теоремы интеграл [2]

Тогда, решение задачи (1) — (3) единственно, так как в как решение задачи Коши с нулевыми данными, а в  как решение однородной задачи .

Вопрос существования решения задачи эквивалентно редуцирован к вопросу разрешимости сингулярного интегрального уравнения

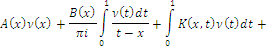
где:  и при  или  может обращаться в бесконечность порядка ниже . Ядро K(x,t) имеет слабую особенность и допускает оценку

Действительно,

Известно, что

для любых и .

Отсюда

Следовательно,

Подвижная особенность ядра  равна , неподвижная . Сумма подвижной и неподвижной особенностей в ядре . Эта особенность меньше 1.

Действительно, при , то есть , что выполняется по условию задачи.

Условие

гарантирует существование регуляризатора, приводящего уравнение (6) к интегральному уравнению Фредгольма второго рода, безусловная разрешимость которого будет следовать из единственности решения задачи. По найденному  можно определить  и решение задачи (1) — (3) в областях и  по формулам

где:

Вывод: в данной работе доказана однозначная разрешимость задачи со смещением для обобщенного уравнения Трикоми в неограниченной области.

Список литературы:

1. Денисова З. Г. Об одной задаче со смещением для уравнения  в неограниченной области. //Дифференциальные уравнения. — 1978. — Т. 14. № 1. — С. 170—173.
2. Кумыкова С. К. Об одной задаче с нелокальными краевыми условиями на характеристиках для уравнения смешанного типа // Дифференциальные уравнения. — 1974. — Т. 10. — № 1, — С. 78—88.
3. Нахушев А. М. О некоторых краевых задачах для гиперболических уравнений и уравнений смешанного типа // Дифференциальные уравнения. — 1969. — Т. 5. — № 1. — С. 44—59.
4. Hardy G., Littlwood J., Somme properties off ractional integrals // Math/ Zs. — 1928. — Bd 27. — № 4. — P. 565—606.