ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ объектом, ОПИСЫВАЕМЫМ СИНГУЛЯРНОЙ сИСТЕМОЙ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Копец Мирослав Михайлович

канд. физ.-мат. наук, доцент, НТУУ «КПИ», г. Киев

Е-mail: miroslav1941@windowslive.com 

1. Введение

Интерес к исследованию систем дифференциальных уравнений, которые не разрешены относительно старших производных, проявился еще в сороковых годах прошлого столетия. Одной из первых работ в этом направлении является статья академика Н. Н. Лузина [10]. Системы подобного типа рассмотрены также в монографии [8, с. 348]. Однако систематическое изучение этих систем фактически началось в начале восьмидесятых годах прошлого столетия. Значительный рост популярности сингулярных систем объясняется их широким применением для решения большого числа практических задач в технике и экономике, а также и тем обстоятельством, что они обладают рядом особенностей по сравнению с обычными системами дифференциальных уравнений. Особо следует отметить, что очень часто к сингулярным системам приводят задачи, которые рассматриваются в теории оптимального управления. Упомянуть все работы, посвященные данной тематике, не представляется возможным. В первую очередь необходимо указать на монографии [3] - [7], [12], [15] - [20]. В них также можно найти обширные библиографические материалы по рассматриваемой тематике. Исторически так сложилось, что основное внимание в процессе исследования сингулярных систем было уделено линейным системам со сосредоточенными параметрами, то есть объектам, поведение которых описывается системами линейных обыкновенных дифференциальных уравнений. Сингулярные системы линейных уравнений с частными производными рассматривались значительно реже. В частности, изучению таких систем посвящена монография [9], а также работы [1], [2]. В них изучаются системы линейных уравнений с частными производными вида

,                                  (1)

где , , -заданные постоянные матрицы размера , -искомая,  вектор-функция, причем , то есть матрица  является вырожденной.

Такие системы называют по-разному: алгебро-дифференциальные системы; вырожденные системы; дифференциально-алгебраические системы; системы не типа Коши-Ковалевской; системы, не разрешенные относительно производных; дескрипторные системы; сингулярные системы; системы с вырождением. Однако независимо от названия всех их объединяет одно общее свойство: матрица  – вырожденная (). Возможны также случаи, когда обе матрицы и – вырожденные. В качестве простого иллюстративного примера, который приводит к сингулярной системе (1), можно рассмотреть телеграфное уравнение [14, с. 215]

.                           (2)

С помощью введения новых переменных

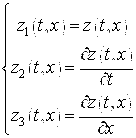
Уравнение (2) можно свести к следующей системе трех уравнений

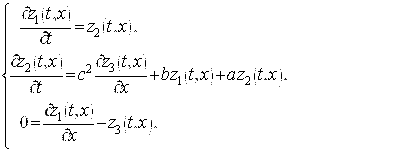
где матрицы , , соответственно равны

, , .

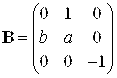К сингулярным системам относят также и такие системы вида (1), когда все три матрицы , ,– прямоугольные матрицы одинакового размера.

2. Постановка задачи оптимального управления

Пусть объект управления описывается следующей системой линейных уравнений с частными производными

,                            (3)

где , ,  – заданные матрицы размера ,  – заданная матрица размера , причем все эти четыре матрицы – постоянные (их элементами являются действительные числа) и . Переменная  ассоциируется со временем, переменная  – пространственная переменная,  – действительный -мерный вектор-столбец, в дальнейшем называемый состоянием системы (3), действительный -мерный вектор-столбец  называется управлением. Предполагается, что управления принадлежат классу кусочно-непрерывных вектор-функций. Для системы (3) задано начальное условие

                                                 (4)

и нулевые граничные условия

, .                                          (5)

Действительное число  и -мерный вектор-столбец  заданы. Считаем, что для каждого заданного управления система уравнений (3) имеет единственное решение, которое удовлетворяет условиям (4) и (5).

Рассмотрим следующий критерий оптимальности

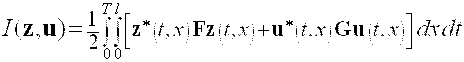
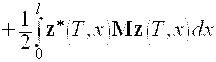,                              (6)

где  означает скалярное произведение векторов  и , то есть 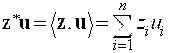,  – заданная симметричная положительно определенная матрица размера  ( следовательно, существует матрица),  также известная симметричная положительно определенная матрица размера ,  – заданное действительное число. Задача оптимального управления объектом, описываемым системой соотношений (3) - (5), состоит в определении  такого управления , при котором функционал (6) принимает наименьшее значение. При этом управление называется оптимальным управлением.

3. Вывод уравнений Эйлера – Лагранжа

Как правило, для нахождения решения задач оптимального управления системами как и со сосредоченными параметрами, так и с распределенными параметрами, используется принцип максимума Л. С. Понтрягина [13, с. 183] или метод динамического программирования Беллмана [11, с. 291]. Оба этих метода предполагают, что система дифференциальных уравнений, которая описывает поведение объекта управления, разрешена относительно производных по времени. В случае сингулярных систем такой возможности нет. Однако можно воспользоваться методом множителей Лагранжа [13, с. 31]. Сущность метода состоит в том, что вместо функционала (6) рассматривается следующий функционал

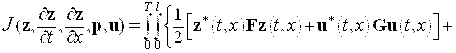
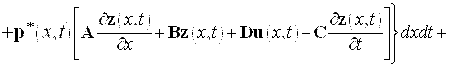
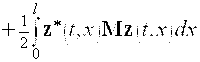,                                      (7)

где  - неизвестная  вектор-функция. Очевидно, что при выполнении соотношения (3) значения функционалов (6) и (7) совпадают. Поэтому задача на условный экстремум для функционала (6) сводится к задаче на безусловный экстремум для функционала (7). Дальше находим выражение для приращения функционала (7).

_{Очевидно, имеем}

.

_.

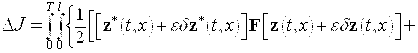
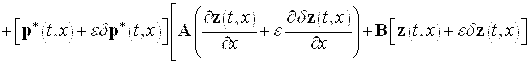
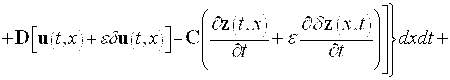
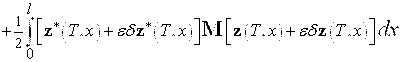
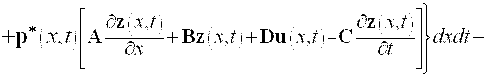
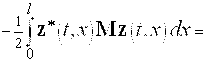
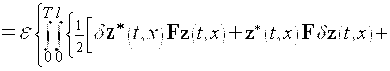
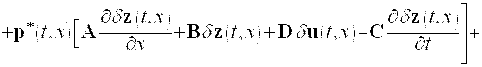
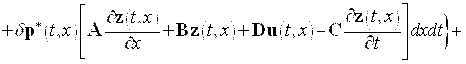
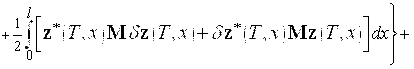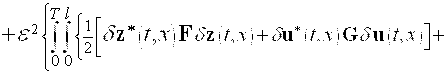
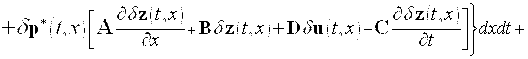
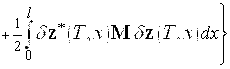Учитывая, что , , , после очевидных преобразований (интегрирования по частям и приведения подобных членов) получим

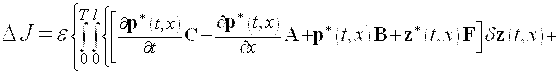
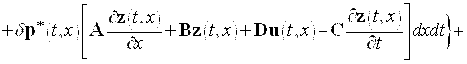
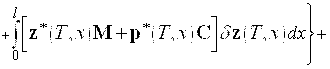
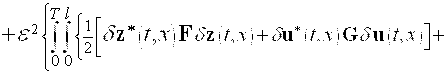
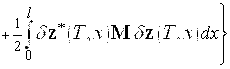_.                                    (8)

Полученное выражение для дает возможность сформулировать следующее утверждение.

Теорема 1. Единственное оптимальное управление , которое реализует минимум функционала (6), определяется из соотношений

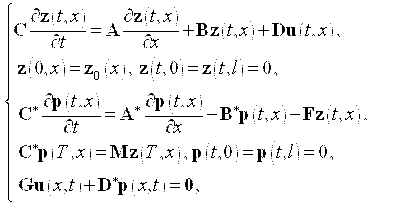                  ₍₉₎

где символ обозначает транспонированную матрицу . Аналогично обозначаются транспонированные матрицы и.

Доказательство. Коэффициент прив соотношении (8) - это первая вариация функционала (7), при  - его вторая вариация, умноженная на . Необходимое условие экстремума функционала (7) - равенство нулю его первой вариации. Это возможно, когда выражения при ,,,равны нулю одновременно. Таким образом получаем систему уравнений (9). Эта система уравнений называется уравнениями Эйлера-Лагранжа. Поскольку справедливо равенство

то, принимая во внимание соотношение (3), приходим к такому равенству

Это означает, что вторая вариация функционала (7) имеет следующий вид

  .

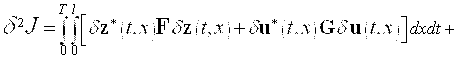
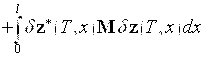С учетом положительной определенности матриц ,,, имеем . Это означает, что управление реализует минимум функционала (7), а значит, и функционала (6). Доказательство единственности оптимального управления следует из таких рассуждений. Предположим, что существует управление , на котором также реализуется минимум функционала (7). Тогда приращение (8) равно нулю. Поскольку в этом случае , то тогда также и . Такое равенство возможно в том случае, когда  и . Отсюда следует, что .

4. Вывод дифференциального уравнения Риккати

Из третьего уравнения этой системы уравнений (9) выражаем  через  () и подставляем в первое уравнение. Получим двухточечную краевую задачу для двух уравнений с частными производными относительно вектор-функций  и :

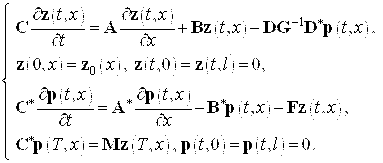                     (10)

Решение последней задачи ищем в следующем виде

,                                                      (11)

где - неизвестная матричнозначная функция. Дифференцируя равенство (11) сначала по переменной , потом  по переменной , получим

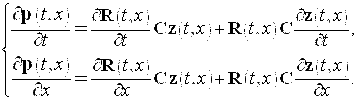                           (12)

Дальше, учитывая первое уравнение из системы (10) и соотношение (11), приходим к такому равенству

После умножения этого соотношения слева на матрицу окончательно имеем

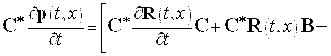
                 (13)

С другой стороны, на основании (10), (11) и (12) подобным образом находим

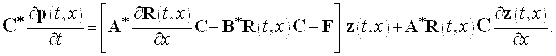      (14)

В соотношениях (13) и (14) левые стороны одинаковы. Следовательно, правые стороны также должны быть равными. В результате имеем следующее равенство

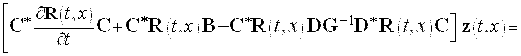
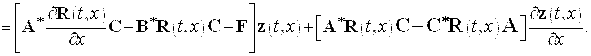
Оно возможно, если выполняются два следующих соотношения

,                                             (15)

.                                               (16)

Обычно для систем со сосредоточенными параметрами уравнение типа (15) известно под названием: матричное дифференциальное уравнение Риккати. В нашем случае имеем  матричное дифференциальное уравнение Риккати с частными производными. Кроме того, появляется еще и уравнение (16). Оно не является тривиальным. Действительно, в случае, когда , где  – единичная матрица, то далеко не всегда справедливо равенство . Дальше, принимая во внимание соотношения

_{получаем следующие дополнительные условия для :}

                           (17)

На основании предыдущих рассуждений приходим к следующему выводу.

Теорема 2. Оптимальное управление  линейно зависит от состояния , то есть справедливо равенство , где матричнозначная функция  является решением уравнений (15) и (16), а также удовлетворяет краевым условиям (17).

Список литературы:

1.            Бормотова О. В., Чистяков В. Ф. В. О методах численного решения и исследования систем не типа Коши-Ковалевской. // Журн. вычисл. матем. и мат. физики. – 2004. – Т. 44, № 8. – С. 1380 – 1387.

2.            Бормотова О. В., Гайдомак С. В., Чистяков В. Ф. В. О разрешимости вырожденных систем дифференциальных уравнений в частных производных. // Изв. вузов. Математика. – 2005. – № 4 (515). – С. 18 – 29.

3.            Бояринцев Ю. Е. Регулярные и сингулярные системы линейных обыкновенных дифференциальных уравнений. – Новосибирск: Наука, 1980. – 222 с.

4.            Бояринцев Ю. Е. Методы решения вырожденных систем обыкновенных дифференциальных уравнений. – Новосибирск: Наука, 1988. – 158 с.

5.            Бояринцев Ю. Е. Линейные и нелинейные алгебро-дифференциальные системы. – Новосибирск: Наука, 2000. – 223 с.

6.            Бояринцев Ю. Е., Орлова И. В. Пучки матриц и алгебро – дифференциальные системы. – Новосибирск: Наука, 2006. – 124 с.

7.            Бояринцев Ю. Е., Чистяков В. Ф. Алгебро-дифференциальные системы. Методы решения и исследования. – Новосибирск: Наука, 1998. – 224 с.

8.            Гантмахер Ф. Р. Теория матриц. – М.: Наука, 1975. – 576 с.

9.            Демиденко Г. В., Успенский С. В. Уравнения и системы, не разрешенные относительно старшей производной. – Новосибирск: Научная книга, – 1998. – 436 с.

10.       Лузин Н. Н. К изучению матричной системы теории дифференциальных уравнений.// Автоматика и телемеханика. – 1940. - № 5. – с. 4 – 66.

11.         Лурье К. А. Оптимальное управление в задачах математической физики. М.: Наука, 1975. – 480 с.

12.         Самойленко А. М., Шкіль М. І., Яковець В. П. Лінійні системи диферен- ціальних рівнянь з виродженнями. – Київ: Вища школа, 2000. – 204 с.

13.         Сиразетдинов Т. К. Оптимизация систем с распределенными параметрами. М.: Наука, 1977. – 480 с.

14.       Фарлоу С. Уравнения с частными производными для научных работников и инженеров: Пер. с англ. – М.: Мир, 1985. – 384 с.

15.       Чистяков В. Ф., Щеглова А. А. Избранные главы теории алгебро-дифференциальных систем. – Новосибирск: Наука, 2003. – 320 с.

16.       Ascher R., Petzold L. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. – USA, Philadelphia, 1998. – 314 p.

17.       Campbell S. L. Singular system of differential equations. Research Notes in Math., No 40. – San Francisco: Pitman, 1980. – 176 p.

18.       Campbell S. L. Singular system of differential equations. II. Research Notes in Math., No 61. – San Francisco: Pitman, 1982. – 234 p.

19.       Dai L. Singular control systems. Lecture Notes in Control and Information Sciences, No 118. – Berlin, Heidelberg, N. Y.: Springer Verlag, 1989. – 332 p.

20.       Kunkel P., Mehrmann V. Differential-Algebraic Equations. Analysis and Numerical Solution. Printed in Germany, 2006. – 377 p.