ПРИМЕНЕНИЕ ТЕОРИИ ОТОБРАЖЕНИЯ ОТРЕЗКА К ИЗУЧЕНИЮ ДИНАМИЧЕСКИХ СВОЙСТВ МАНИПУЛЯТОРА ФАЗЫ С ФАП

Лебедева Лариса Владимировна

канд. физ.-мат. наук, доцент ВГАВТ, г. Н. Новгород

Е-mail:

Существует ряд систем фазовой синхронизации (СФС), содержащих временной такт работы, математическая модель которых может быть представлена в виде разностного уравнения, например,

                                       1)

К таким системам относятся, в частности, одноконтурные системы импульсно-фазовой автоподстройки частоты (ФАП) с элементом типа "выборка-запоминание" [9, с. 63]; [1, с. 161]; [2, с. 771], ФАП с ключом с фиксирующим элементом [11, с. 21], ... . Развитая теория отображений окружности и отрезка [7, с. 215]; [8, с. 32]; [10, с. 61]; [11, с. 289]; [12, с. 21] позволяет установить основные динамические свойства таких СФС. В настоящей работе представлены результаты изучения особенностей поведения, так называемого, манипулятора фазы с ФАП [3, с. 46];[ 4, с. 56]. На основе известных дифференциальных уравнений, описывающих работу этой системы, получена математическая модель в виде разностных уравнений и проведен анализ динамических свойств системы.

Математическая модель.

В качестве манипулятора фазы рассматривается система ФАП, дополненная вторым фазовым детектором (ФД), фазовращателями и коммутатором. Блок-схема такого манипулятора изображена на рис. 1. Сигнал от источника колебаний 1 (эталонного генератора) разветвляется на два идентичных коммутируемых канала 4 и 5. В соответствии с передаваемой информацией коммутатор 6 попеременно подключает вход управителя частоты 7 (и подстраиваемого генератора 8) к выходам фазовых детекторов 4 и 5. При этом замыкается либо кольцо ФАП с фазовращателем 2 (), либо кольцо с фазовращателем 3 (). После окончания переходного процесса в кольце ФАП фаза ПГ изменится либо на угол , либо на угол , т. е. на угол, создаваемый фиксированными фазовращателями на входе системы в цепи эталонного сигнала. Следовательно, любая желаемая глубина манипуляции  достигается выбором соответствующих фазовых сдвигов в фазовращателях 2 и 3. Период коммутации T считается постоянным. При упрощающем предположении об отсутствии фильтра нижних частот работа такого манипулятора фазы описывается [3, с. 46]; [4, с. 56] системой уравнений:

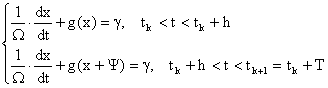                                    ( 2)

Здесь  текущая разность фаз генераторов,  - полоса синхронизма,  - нормированная начальная расстройка. Принято считать, что фазовые детекторы 4 и 5 обладают одинаковыми нормированными характеристиками . На основе решений системы (2) получим разностное уравнение, описывающее работу манипулятора фазы. Во втором уравнении сделаем замену  (так как , то ): . Пусть решение первого уравнения есть функция , тогда решением второго является функция . Пусть в начальный момент времени  значение функции , тогда значения функций в момент  определяются как  и , а в конце периода при  имеют вид . =  Следовательно, работа манипулятора фазы описывается разностным уравнением: , где функция  есть решение уравнения , а величины  являются параметрами.

Рассмотрим наиболее часто встречающийся случай, предположив, что характеристика фазового детектора косинусоидальна, т. е. . Тогда первое уравнение примет вид: . Заменим  на  и запишем первое уравнение в виде . С учетом начального условия  его решение можно записать в виде:

                                        ( 3)

Здесь , , , , , . Найдем явное выражение для функции .

Рассмотрим случай |.  Введем новую переменную , т. е. , первое равенство соотношений (3) запишем в виде: , т. е. 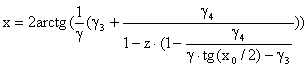. Получили, что для случая  искомое отображение

имеет вид:

                       (4)

где , , , .

Рассмотрим случай . Пусть , т. е. . Сокращая второе уравнение системы (3) на общий множитель, получаем . Возьмем тангенс от обеих частей: . После преобразований получаем 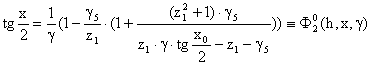, 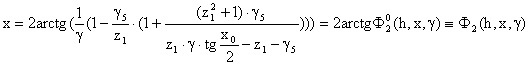. Искомое отображение при

 имеет вид:

                                            (5)

Динамические свойства манипулятора фазы.

Как известно [7, с. 215]; [8, с. 32]; [12, с. 21]; [2, с. 771], динамическое поведение системы, описанной отображением (1), зависит, прежде всего, от того является отображение гомеоморфизмом (т. е. отображение взаимно однозначно) или эндоморфизмом. Под траекторией отображения  понимается [2, с. 771] последовательность точек , , , … Назовем траекторию отображения -циклом, если , но ни для какого  равенство  не выполняется (предполагается, что  – любое натуральное, а – любое целое числа). -циклы при  соответствуют вращательным, а при  - колебательным движениям. Задача исследования сводится к изучению -зон – областей параметров, при которых существуют устойчивые -циклы.

Установим, являются ли отображения (4) и (5) гомеоморфизмами или эндоморфизмами. Учитывая, что величины  и  положительны, получаем  =  для всех  и . Т. е. при всех значениях  имеет место соотношение  = . Доказана

ЛЕММА 1. При  работа системы (1) описывается уравнением (4). Для всех  имеет место равенство , где .

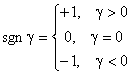Рассмотрим случай . Введем обозначения , ,  и рассмотрим производную . Имеем: . =  = 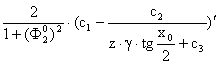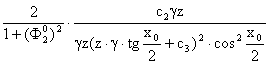, т. е.  для всех значений . Доказана

ЛЕММА 2. При  работа манипулятора фазы описывается разностным уравнением (5). Для всех  справедливо неравенство .

Из лемм 1 и 2 получаем следующие утверждения. Отображения (4) и (5) являются гомеоморфизмами. К ним применима теория Майера [7, с. 215] и теория числа вращения [8, с. 32]. Отображения могут иметь колебательные неподвижные точки периода один () или два  и вращательные неподвижные точки любого периода, причем -зоны с разными числами  не пересекаются. Это означает, что манипулятор фазы может работать в режиме синхронизма (возможен режим с глобальной асимптотической устойчивостью синхронизма), квазисинхронизма, подстройки под комбинационную частоту, режиме ложного захвата и режиме биений. Особенностью такой системы является достаточно простая структура колебательного притягивающего множества, определяющего характеристики стационарного режима квазисинхронизма.

Список литературы:

1.             Белых В. Н. Модели дискретных СФС и их исследование. – В кн. Системы фазовой синхронизации/ Под ред. В. В. Шахгильдяна, Л. Н. Белюстиной. М.: Радио и связь, 1982, с. 161-162

2.            Белых В. Н., Лебедева Л. В. Исследование одного отображения окружности. – ПММ, 1982, т. 46, вып. 5, с. 771-776

3.            Капранов М. В., Рихтер С. Г. Фазовая автоподстройка частоты в  режиме манипуляции фазы. – В сб докладов научно-техн. конф. по итогам научно-исследовательских работ за 1966-1967 гг. в МЭИ, М. 1967, с. 46-52

4.            Капранов М. В., Рихтер С. Г. Высокоскоростной режим манипулятора фазы с системой ФАП – В сб докладов научно-техн. конф. по итогам научно-исследовательских работ за 1966-1967 гг. в МЭИ, М. 1967, с. 56-62

5.            Лебедева Л. В. О динамике дискретных одномерных систем фазовой синхронизации. Респ.сб. «Теоретическая радиотехника», Львов, 1986, с. 46-49

6.            Лебедева Л. В. Определение наличия периодической траектории унимодального отображения отрезка / Межвуз. сб. «Математическое моделирование и оптимизация», Н. Новгород, ННГУ, 1996, с. 31-38

7.            Майер А.Г. Грубое преобразование окружности в окружность. – Ученые записки ГГУ, 1939, вып. 12, с. 215-226

8.            Нитецки Э. Введение в дифференциальную динамику. М.: Мир. 1975, 304 с.

9.            Системы фазовой синхронизации с элементами дискретизации / Под ред. В. В. Шахгильдяна  М.: Радио и связь, 1989

10.        Шарковский А. Н. Сосуществование циклов непрерывного преобразования прямой в себя. УМЖ, 1964, т. 16, №1, с. 61-72

11.       Шахгильдян В. В., Петров В. А. Анализ работы системы синхронизации 1 порядка с ключом. – В кн. Фазовая синхронизация / Под ред. В.В.Шахгильдяна, Л.Н.Белюстиной. М.: Связь, 1975, с. 289-294

12.       Collet P. and Eckmann J.-P. Iterated Maps on the Interval. Dynamical Systems. Basel. Birkhauser. 1980

13.       R. May. Simple mathematical models with very complicated dynamics. Nature. Vol.251, June.10, 1976