ОДНА ОБРАТНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ПУАССОНА

Павлов Геннадий Александрович

канд. физ.-мат. наук, доцент, АГАУ, г. Барнаул

Абакумова Наталья Александровна

канд. социол. наук, АГАУ, г. Барнаул

E-mail: aba78@mail.ru

В плоском случае рассматривается задача определения правой части уравнения Пуассона. Приведены примеры неединственности решения задачи, а также теоремы существования решения. В случае уравнения Гельмгольца подобная задача рассматривалась в работах [1, 2] а также в монографии [3, с. 651, c. 675, c. 676].

Пусть ,  (за исключением быть может отдельных точек).

                              (1)

Поставим задачу определения функции , если выполнены условия

                                                  (2)

где  кривая , причем  есть проекция  на ось , ,  – граница.

Вначале покажем, что задача имеет, вообще говоря, неединственное решение. Легко проверить, что если функция  знакопеременная, то решение задачи определяется неединственным образом.

Пример 1. Пусть , ,

,

 удовлетворяет уравнению (1), условиям (2), ,  – прямая .

Тогда наряду  данному уравнению удовлетворяет  (решение

Итак, условие  является в некотором смысле необходимым условием. Заметим, что если вместо условия будем рассматривать условие: нормальное производное на ней равно нулю, то условие  уже не будет достаточным.

Пример 2. , ,

.

Здесь наряду с , задаче удовлетворяет  (решение ).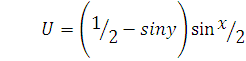

Следующий пример, хотя и не относится к уравнению Пуассона, но по видимому, подстерегает нас, что условие  явно является недостаточным для однозначного определения

Пример 3. Пусть , где

  или 2 произвольное число.

.

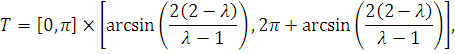
Здесь наряду с  есть решение  (решение

В примере 3 наиболее интересный случай, когда  не является собственным значением оператора Лапласа . Интересно рассмотреть случай Перейдем к изучению задачи. Отметим вначале, что если  (заданная функция) достаточно гладкая, то заменой переменной  уравнение (1) можно свести к эллиптическому уравнению второго порядка с коэффициентами зависящими от , , где в правой части будет стоять уже функция  задача определения правой части  будет неединственная. Заметим, что уравнение в этом случае может быть записано в виде

.

И для того, чтобы для этого уравнения соблюдался принцип максимума, необходимо, в случае , чтобы  была супергармонической функцией.

В связи с этим, возникает гипотеза, если  супергармоническая функция, то задача определения , возможно, не может иметь больше одного решения.

Выпишем эллиптическое уравнение общего вида, с достаточно гладкими коэффициентами, для которого справедлив принцип максимума, где задача определения правой части  с  имеет не более одного решения. В общем в виде:

.                    (3)

Действительно, в этом случае решение можно записать в виде

,                        (4)

где  – решение однородного уравнения, а  удовлетворяет для  уравнению

,

.                                    (5)

Тогда  и кроме того

,

то есть функция  достигает максимума (минимума) и на  и он очевидно, если  больше нуля, откуда получаем противоречие.

Рассмотрим теперь уравнение (1) с ,  и покажем, что решение задачи существует (задача нахождения ). Не теряя общности, можно считать .

Предположим, что .

Лемма. Существует единственное решение задачи правой части , при этом обратное отображение  является ограниченным оператором из

Замечание 1. Решение задачи можно искать в другом виде. Заметим, что так как , , то

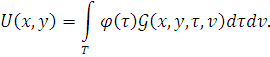
Откуда для нахождения  получаем уравнение, эквивалентное задачи

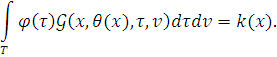
Из леммы вытекает, что существует ограниченный оператор из  такой, что .

Рассмотрим произвольную функцию , ,  и обозначим , .

Теорема. Пусть , , , .

Тогда существует такое число , что для всех  для любой заданной функции , найдется единственная функция , удовлетворяющая условию (1).

Замечание 2. Отметим, что если вместо уравнения (1) рассмотрим уравнение , где  – заданная функция, , , ,  – супергармоническая функция, то задача определения функции  при условиях ,  имеет не более одного решения.

В случае , когда  решение задачи легко получить методом разделения переменных.

Замечание 3. К рассмотренной задаче может быть сведена задача о единственности определения коэффициента  при уравнении

.

Для этой задачи имеют место аналогичные примеры неоднозначного определения .

Список литературы:

1.  Запреев А. С. Теорема единственности решения плоской обратной задачи для уравнения Гельмгольца // Некорректные математические задачи и проблемы геофизики. – Новосибирск, 1976. – С. 46 - 63.

2.  Запреев А. С., Цецохо В. А. Обратная задача для уравнения Гельмгольца. – Новосибирск, 1976. – 18 с. (Препринт / АН СССР. Сиб. Отд-не. ВЦ; № 22).

3.  Лаврентьев М.М., Савельев Л.Я. Теория операторов и некорректные задачи. Новосибирск: изд-во Ин-та математики, 1999. 702 с.