Статья опубликована в рамках: I Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 20 декабря 2011 г.)
Наука: Математика
Секция: Геометрия и топология
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Методика изучения геометрических преобразований в вузе с использованием информационных технологий
Ганеева Айгуль Рифовна
канд. пед. наук, и.о. доцента кафедры математического анализа, алгебры и геометрии филиала КФУ в г. Елабуга
E-mail: aigul_ganeeva@mail.ru
В современном мире с каждым днем информационные потоки все больше проникают в различные сферы деятельности. В связи с этим необходимо пересмотреть систему профессиональной подготовки будущих учителей. Уже сейчас школе нужны квалифицированные специалисты с высоким уровнем образованности, способные переключаться с одного вида педагогической деятельности на другой. От современного учителя требуется не только обширные, но и, прежде всего, систематизированные знания и умения [3].
Подготовка будущих учителей в вузе должна быть основана на творческом развитии личности, способности к постоянному самосовершенствованию и саморазвитию.
Информационная культура будущих учителей должна формироваться все годы обучения и не в рамках одного предмета, а в наборе профилирующих курсов.
Студентов необходимо заинтересовать предметом. Базовая подготовка, которую получили студенты в школе очень низкая. Информационные технологии помогут успеть повторить на занятии школьный материал, а потом изучить соответствующую тему вузовской геометрии.
При традиционном чтении лекций и проведении практических занятий по геометрии требуются многочисленные построения, с использованием чертежных инструментов. Это занимает большое количество времени. Используя информационные технологии можно разнообразить занятия по геометрии красочными, анимированными слайдами.
Информационные технологии позволяют рассмотреть все случаи решения той или иной задачи, доказательство теоремы, рассмотреть частный случай и т. д.
Средства мультимедиа способствуют более глубокому и осознанному усвоению изучаемого материала, так как студент, освоив основные понятия на лекции, сможет без труда вернуться к просмотренному материалу для закрепления или повторения его во внеучебное время.
При традиционном обучении геометрии многие студенты испытывают затруднения, цели обучения часто не достигаются, и одной из причин этого, по мнению многих методистов, является преобладание аналитических методов изучения. Психологически обоснованно, что при изучении систематического курса геометрии, целесообразно опираться на наглядно-действенное мышление и практическую деятельность студентов и отдавать предпочтение конструктивному подходу в качестве возможного пути совершенствования преподавания систематического курса геометрии. Средством реализации конструктивного подхода может являться система конструктивных задач, обеспечивающая возможность изучения геометрических преобразований и их применения [2, c. 6].
На занятиях, посвященных изучению геометрических преобразований и его видов преподавателю, как правило, приходится рисовать на доске множество различных фигур и пытаться изобразить процесс их преобразования. Применение PowerPoint в таких случаях экономит время на занятиях, предоставляя анимационные чертежи, повышает наглядность по сравнению со статичной картинкой на доске.
Геометрические преобразования отражают общие закономерности явлений природы. Такие преобразования как осевая, центральная симметрия, параллельный перенос, поворот – есть обобщение наблюдаемых в природе явлений. Понятие движения взято из реальной действительности и является отражением свойств реальных предметов. Благодаря этому изучение геометрических преобразований предполагает возможность широкого использования задач прикладного характера и практического содержания. Применяя данные геометрические преобразования можно создавать необыкновенной красоты орнаменты, эскизы для паркетов.
Очарование красивыми образами помогает убедить школьников в востребованности знания о геометрических преобразованиях плоскости. Кроме того, следует заметить, что для геометрии эта тема важна и интересна сама по себе, не только в связи с ее применением для построения узоров. Так мотивируется необходимость изучения геометрических преобразований в школьном курсе геометрии. Всю красоту природы и прикладной направленности геометрических преобразований можно продемонстрировать используя информационные технологии [4, c. 220].
В качестве примера рассмотрим поэтапно лекцию по геометрии на тему: «Инверсия». С инверсией студенты впервые встречаются в вузе. Это геометрическое преобразование отличается от других геометрических преобразований. Необходимо наглядно продемонстрировать всю красоту инверсии.
1) После ввода определения инверсии, говорим, что оно является инволютивным преобразованием. Устно на слайдах используя анимацию можно продемонстрировать процесс построения образа точки М при инверсии и прообраза точки ![]() .
.
2) Свойства инверсии (рис. 1).

Рисунок 1.
3) Далее на доске проводим вывод формул преобразования инверсии, если базовая окружность имеет центр с координатами (0;0). Сразу после вывода данных формул на слайде можно продемонстрировать формулы преобразования, если центр базовой окружности имеет произвольные значения.
4) Аналитический вывод двух предложений: 1) прямая не проходящая через центр инверсии переходит в окружность, проколотую в точке О; 2) окружность проколотая в точке О, переходит в инверсии в прямую, не проходящую через точку О. На слайдах можно продемонстрировать различные случаи расположения данных прямых и окружностей относительно данной базовой окружности (рис. 2).
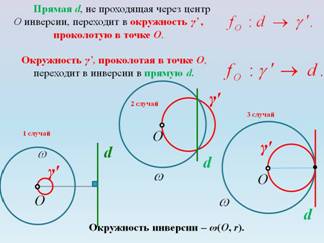
Рисунок 2.
5) Аналитический вывод предложения: окружность не проходящая через центр О инверсии переходит в окружность, также не проходящую через точку О. На слайдах можно продемонстрировать различные случаи расположения данной окружности относительно данной базовой окружности (рис. 3).
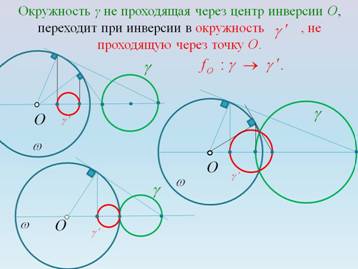
Рисунок 3.
6) Доказательство теоремы: угол между данными линиями конгруэнтен углу между линиями инверсными данным. Очень тяжело представить данную теорему геометрически, поэтому можно перед доказательством данной теоремы рассмотреть на слайде устно частный случай (рис. 4).
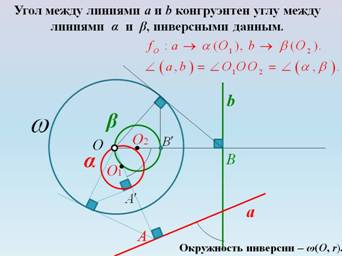
Рисунок 4.
Аналогично можно проводить занятия и по другим темам геометрии с использованием информационных технологий.
Список литературы:
1.Геометрия. Учеб. пособие для студ. I курса физ.-мат. факультетов пед. инсти-в / В. Т. Базылев и др. М., «Просвещение», 1974 – 351 с.
2.Клубничкина О. А. Изучение геометрических преобразований в общеобразовательной школе (В условиях дифференцированного обучения): дис. ... канд. пед. наук. М., 2001 – 199 c.
3.Косино О. А. Формирование профессиональной компетентности учителя в области элементарной математики в условиях интеграции педагогических и информационных технологий // Современные проблемы науки и образования. 2009. № 2. [электронный ресурс] – Режим доступа. – URL: http://www.science-education.ru/29-1070 (дата обращения: 20.12.2011).
4.Методика обучения геометрии: Учеб. пособие для студ. высш. пед. учеб. заведений / В. А. Гусев, В. В. Орлов, В. А. Панчищина и др.; под ред. В. А. Гусева. – М.: Издательский центр «Академия» – 368 с.
дипломов

Оставить комментарий