ПРИМЕНЕНИЕ ТЕОРИИ ИНЖЕНЕРНОГО ДИСКРИМИНАНТА В ПРИКЛАДНЫХ РАСЧЕТАХ

Попова Людмила Сильвестровна

к.т.н., доцент, ФГБОУ ВПО «ВятГУ» г. Киров

Синицына Ольга Владимировна

к.т.н., доцент, ФГБОУ ВПО «ВятГУ» г. Киров

Основной задачей разработки сложносоставных плоских и пространственных обводов является создание их оптимальной математической модели в рамках существующих систем автоматизированного проектирования. Для модернизации систем автоматизированного расчета и управления работой различных объектов и процессов необходимы планомерные исследования в этой области.

Чтобы достигнуть оптимальных результатов на стадии проектирования самих объектов, принята следующая последовательность конструктивных действий:

1.  на основании заданной графической информации и вводных технических условий проектируют математическую модель разрабатываемого объекта;

2.  по полученным в результате апробации объекта эмпирическим данным,  производится  доработка его  требуемых свойств.

При проектировании сложносоставных поверхностей обтекаемых технических конструкций типа судов и летательных аппаратов, прежде всего, необходимо учесть комплекс специальных требований. Особые условия, предъявляемые при конструировании обводов таких поверхностей с заданной степенью гладкости, определяют создание новых графических и аналитических алгоритмов их моделирования.

В предыдущих работах [2, с. 322] предлагается описывать сложные геометрические поверхности в матричной форме записи. Аналитическое описание поверхности в матричной форме обеспечивает достаточно высокую степень формализации решения задач при стыковке кусков поверхностей с заданной степенью гладкости в плоскостях произвольного положения.

Для разработки сложносоставных поверхностей большое практическое применение нашли кривые и поверхности второго порядка, заданные в неявном виде. Если пространственный обвод составлен из поверхностей второго порядка, то линия касания кусков поверхностей также будет второго порядка.

Рассмотрим метод, основанный на использовании сегментов конических сечений, которые удовлетворяют условиям сопряжения и касания в нескольких точках. Как известно, кривые второго порядка можно получить сечением конической поверхности вращения различными  плоскостями. В зависимости от расположения секущей плоскости и исходной конической поверхности получаем:

·     окружность, если секущая плоскость расположена перпендикулярно оси вращения конуса;

·     эллипс, если секущая плоскость пересекает все образующие конуса конуса;

·     парабола, если секущая плоскость параллельна одной образующей конуса;

·     гипербола, если секущая плоскость параллельна двум образующим конуса.

Для получения искомого уравнения используются сегменты конических сечений, которые удовлетворяют условиям сопряжения и касания в нескольких заданных точках.

Конические сечения общего вида описываются уравнением второго порядка в неявной форме [3, с. 18]:

                 (1)

Вид кривой данного сечения определяется коэффициентами A B C D E L. Для того чтобы найти эти коэффициенты необходимо наложить пять независимых условий, и решить соответствующие уравнения для отношений этих коэффициентов к одному из них. Эта операция достаточно трудоемка.

Чтобы избежать решения системы уравнений можно воспользоваться классическим приемом, который показывает преимущества уравнений, заданных в неявном виде [4, с. 81].

Пусть два конических сечения (рис. 1) заданы уравнениями f₁  (x,y)=0 и f₂  (x,y)=0, или кратко f₁ =0, f₂ =0.

Эти кривые пресекаются в четырех точках, через которые можно провести пучок конических сечений, в том числе вырожденные конические сечения, которые получаются в результате пересечения конуса плоскостью, проходящей через его вершину.

Рисунок 1.

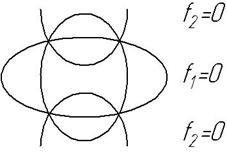
Уравнение этого пучка имеет вид:

(1–λ) f +λ f =0,

где λ – инженерный дискриминант, с помощью которого можно регулировать форму кривых данного пучка.

Уравнение действительно для точек, принадлежащих f₁ =0 и f₂ =0. Это уравнение удовлетворяет еще одно коническое сечение, проходящее через точки пересечения кривых f₁ =0 и f₂ =0 при любых значениях λ.

В инженерном варианте кривая второго порядка может быть определена треугольником АВС и дискриминантом λ. Рассмотрим данное положение на примере (рис. 2). Зададим кривую l второго порядка точками A, С и F, а также касательными l₁ и l₂ (АВ и ВС) в точках A и С.

Рисунок 2.

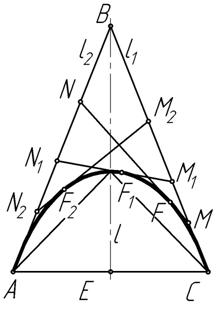
Выберем точку F внутри треугольника AВС, тогда коническое сечение образует непрерывную кривую между точками A и С внутри треугольника. Если точка F делит пополам прямую, соединяющую середины отрезков АВ и ВС, то коническое сечение является параболой. Если F находится между этой параболой и прямой AС, то получается эллипс. Если же эта точка находится за пределами параболы, то получается гипербола.

Задавая исходное положение точки F определяем коэффициент λ, который находится из отношения:

FЕ/FВ=λ,

где λ – инженерный дискриминант дуги AС кривой второго порядка, заданного соприкасающимся треугольником AВС и точкой F.

Выбирая различные положения точки F, можно задавать форму дуги проектируемой кривой второго порядка – эллипса, параболы, гиперболы.

Рассмотрим алгоритм проектирования кривой l, заданной координатами требуемого количества точек.

Известно, что данная кривая l проходит через точки  A, C и F. Прямые АВ и ВС (l₁ и l₂) - это касательные прямые к кривой l, проведенные в точках А и С, а прямые Мi Ni , касательные к кривой l в точках Fi.

Точка F, удовлетворяет системе трех отношений:

                       (2)

Построим в любой точке Fi кривой l касательную прямую Мi Ni. Обозначим на ней отрезки FN и FM так, чтобы NMK=µ. Если через полученные точки M и N провести касательные к кривой l, то получим треугольник АСВ, в котором сохраняются равенства (2).

Представленный алгоритм дает возможность строить точки кривой l, находящиеся как внутри треугольника АСВ, так и вне его.

Одной из задач современной прикладной геометрии является решение вопроса аналитического и графического задания замкнутых контуров сложных форм. При проектировании фюзеляжа самолета, конфигурация каждого сечения составляется из кривых второго порядка, которые имеют в местах соединения общие касательные и одинаковый радиус кривизны. Решение задачи сводится к построению кривых с помощью фигуры постоянных элементов, состоящих из точки F и соприкасающегося треугольника AВС [1, c. 45, 46]. 

Рассмотренный алгоритм позволяет получить уравнения кривых, аппроксимирующих с заданной точностью контуры теоретических поперечных сечений (например, контуры шпангоутов фюзеляжа самолета). 

Разработанный нами математический аппарат геометрического моделирования сложносоставных обводов может быть также успешно применен для контроля вычислений траектории полета геометрических объектов на далекие расстояния.

Рассмотрим, например, варианты полетных траекторий летательного аппарата при перелете с одной планеты на другую. По геометрии Лобачевского, с учетом искривления пространства, траектория полета рассматриваемого объекта представляет собой одну из кривых на поверхности конуса — эллипс, гиперболу или параболу.

Если летательный аппарат должен облететь исследуемую планету и возвратиться, то его полетная траектория будет представлять собой эллиптическую кривую. При запланированной посадке объекта на планету аппарату следует совершать полет по параболе.

На рис. 3 рассмотрена условная полетная траектория летательного аппарата по вариантной кривой второго порядка АВ.

Рисунок 3.

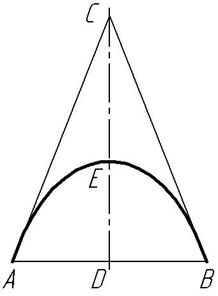
Чтобы рассчитать перелет геометрического объекта из точки А в точку В по параболе, гиперболе или эллипсу используем отношения инженерного дискриминанта λ.

Для определения графического дискриминанта λ сформируем треугольник АВС. Сначала соединим точки А и В прямой линией, а затем в концевых точках дуги проведем касательные прямые и медиану С D. Отметим на медиане точку Е, как точку пересечения медианы с дугой АВ.

Отношение отрезков DE к CD называется графическим или инженерным дискриминантом λ.  

Варианты значений отношений λ=DE/CD инженерного дискриминанта и дают нам решения поставленной задачи.

Рассматриваемая точка Е находится в треугольнике AВС и принадлежит коническому сечению, образующему непрерывную кривую между точками A и В внутри треугольника.

Если точка Е делит пополам прямую, соединяющую середины отрезков АС и СВ, то проходящее через эту точку коническое сечение является параболой.

Если точка Е находится между этой параболой и прямой СD, то полученная кривая будет эллипсом.

Если же эта Е точка находится за пределами параболы, то проходящая через эту точку коническая кривая будет гиперболой.

Таким образом, выбор точки Е напрямую связан со значениями инженерного дискриминанта λ, который находится из отношения DE к CD .

Из аналитической геометрии известно, что по числовым значениям инженерного дискриминанта исходного соприкасающегося треугольника AСВ с точкой Е, определяется характер кривой второго порядка дуги АВ

Например, если значение дискриминанта находится в пределах 0<λ<0,5, то коническая кривая будет эллипсом. Если значение дискриминанта λ=0,5, то расчетная кривая - парабола. А если значения инженерного дискриминанта рассматриваются в пределах от 0,5<λ<1, то кривая второго порядка - гипербола.

Такой вариант моделирования траектории полета позволяет не только рассчитать траекторию пути летательного аппарата, но и сократить количество затратного топлива, уменьшить сопротивление внешних факторов, таких как температура, притяжение и так далее.

Таким образом, оптимальная математическая модель проектируемого обвода полетной кривой позволяет перейти к автоматической системе увязки задающих его параметров.

Опираясь на графические построения, следует разрабатывать всевозможные алгоритмы математического решения поставленных задач. Выбранный подход в процедуре формализации указанной выше задачи позволяет использовать менее энергоемкие программы, благодаря чему проектирование становится более экономичным.

Список литературы:

1.Левицкий В. С. Аналитические методы в инженерной графике [Текст] : учеб. пособие по курсу «Инженерная графика» для слушателей ФПКП / В. С. Левицкий. - М.: Изд-во МАИ, 1978. – С. 43-47.

3.Построение плоского обвода второго порядка с помощью инженерного дискриминанта [Текст] / Л. С. Попова, О. В. Синицына // Наука - производство - технологии - экология : всеросс. ежегод. науч.-техн. конф.. Сб. материалов в 7 т. Т. 4. ФАМ, ФСА / ВятГУ. – Киров, 2008. - С. 321-323.

4.Попова Л. С. Некоторые вопросы проектирования поверхностей технических конструкций [Текст]: дисс. … канд. техн. наук: 05.01.01:защищена  18.06.1981: утв. 30.09.1981/ Л. С. Попова.- М., 1978. - Библиогр.: с. 16-26.

5.Синицына О. В. Матричные методы конструирования обводов и поверхностей [Текст]: дисс. … канд. техн. наук: 05.01.01:защищена  12.01.1996: утв. 19.09.1995/ О. В. Синицына. - М.: Изд-во МАИ, 1995. – С. 79-85.