Одной из главных составляющих процесса анализа инвестиционных проектов является анализ их коммерческой эффективности. На основе построения математической модели пакета предполагаемых инвестиций и применении критериев эффективности, использующих дисконтированные денежные потоки, рассматривается метод оптимизации пакета реальных инвестиций [1]. Исходными данными математической модели являются: денежный поток 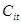, где i – номер инвестиционного проекта (изменяется от 1 до m), t – интервал времени (изменяется от 0 до Т), r – ставка процента. Для построения математической модели обозначим неизвестные. За  примем долю финансового участия компании-инвестора в финансировании i-го проекта (). Среди критериев эффективности пакета реальных инвестиций доминирующую роль играют следующие:

1)                  Сумма дисконтированных чистых поступлений NPV:

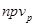, где - предельная сумма дисконтированных чистых поступлений;

2)                  Внутренняя норма доходности IRR:

, где cc – средневзвешенная стоимость капитала;

3)                  Индекс рентабельности PI:

, где - предельное значение индекса рентабельности;

4)                  Дисконтный срок окупаемости DPP:

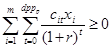, где - предельное значение срока окупаемости.

5)                  Сумма наращенных чистых поступлений NTV:

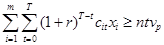, где - предельная сумма наращенных чистых поступлений;

6)                  Модифицированная внутренняя норма доходности MIRR (применяется в тех случаях, когда в пакете из m рассматриваемых инвестиций, присутствуют проекты с неординарными денежными потоками):

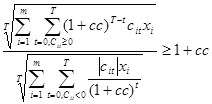 (cc – средневзвешенная стоимость капитала).

Для построения оптимизационной задачи возьмём один из критериев в качестве целевой функции, а остальные в виде ограничений. Так, если NPV – целевая функция, то с учётом ограничений по сумме инвестиций по периодам t (обозначим 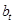- предельные суммы инвестиций по периодам t) получим следующую линейную модель формирования оптимального пакета инвестиций.

Целевая функция:

.

Ограничение по внутренней норме доходности:

.

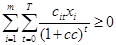Ограничение по индексу рентабельности:

.

Ограничение по дисконтному сроку окупаемости:

.

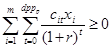Ограничение по сумме наращенных чистых поступлений:

.

Ограничение по модифицированной внутренней норме доходности

.

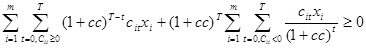Ограничения максимальных сумм инвестиций по периодам:

.

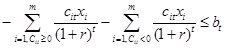Долевые условия:

.

Если в качестве целевой функции выбран индекс рентабельности (нелинейная функция), то задача приводится к линейной путём введения новых переменных:

;

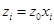
После подстановки переменных 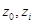 вместо получаем линейную задачу оптимизации пакета реальных инвестиций по критерию максимума индекса рентабельности.

Целевая функция:

.

Ограничение по сумме дисконтированных чистых поступлений:

.

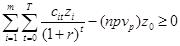Ограничение по внутренней норме доходности:

.

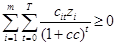Ограничение по дисконтному сроку окупаемости:

.

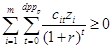Ограничение по сумме наращенных чистых поступлений:

.

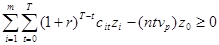Ограничение по модифицированной внутренней норме доходности

.

Ограничения максимальных сумм инвестиций по периодам:

.

Зависимость, связывающая переменные 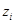между собой:

.

Долевые условия:

.

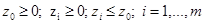После определения оптимальных значени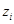й и 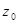 доли участия в инвестиционных проектах  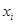вычисляются по формулам , i=1,…,m.

Линейная модель с внутренней нормой доходности в качестве целевой функции имеет вид:

Целевая функция:

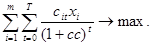
Ограничение по сумме дисконтированных чистых поступлений:

.

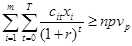Ограничение по индексу рентабельности:

.

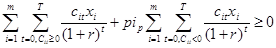Ограничение по дисконтному сроку окупаемости:

.

Ограничение по сумме наращенных чистых поступлений:

.

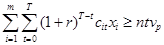Ограничение по модифицированной внутренней норме доходности

.

Ограничения максимальных сумм инвестиций по периодам:

.

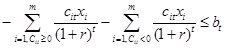Долевые условия:

.

При оптимизации по критерию суммы наращенных чистых поступлений математическая модель имеет следующий вид:

Целевая функция:

Ограничение по сумме дисконтированных чистых поступлений:

.

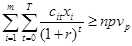Ограничение по внутренней норме доходности:

.

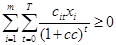Ограничение по индексу рентабельности:

.

Ограничение по дисконтному сроку окупаемости:

.

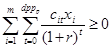Ограничение по модифицированной внутренней норме доходности

.

Ограничения максимальных сумм инвестиций по периодам:

.

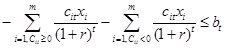Долевые условия:

.

Если в качестве целевой функции взять модифицированную внутреннюю норму доходности, то получим следующую задачу:

Целевая функция:

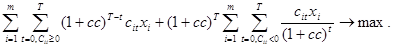
Ограничение по сумме дисконтированных чистых поступлений:

.

Ограничение по внутренней норме доходности:

.

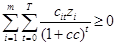Ограничение по индексу рентабельности:

.

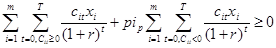Ограничение по дисконтному сроку окупаемости:

.

Ограничение по сумме наращенных чистых поступлений:

.

Ограничения максимальных сумм инвестиций по периодам:

.

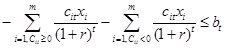Долевые условия:

.

Задачи оптимизации пакета инвестиций решаются с помощью табличного процессора “Excel”, либо с помощью специальной компьютерной программы ”Оптимум”, разработанной в МГИМО.

Повышению обоснованности принимаемых инвестиционных решений способствуют следующие результаты данной работы. Обобщённая математическая постановка позволяет применить одновременно большое количество критериев эффективности для формирования оптимального пакета инвестиций из множества проектов с заданными денежными потоками. Линейная постановка позволяет для получения оптимального решения ограничиться широко распространёнными алгоритмами линейного программирования.

Список литературы:

1.  Российская экономика: пути повышения конкурентоспособности: коллективная монография/Моск. гос. инст-т междунар. отнош. (Университет) МИД России; отв. ред.: А.В.Холопов. -М. : Издательский дом Журналист, 2009. -690 с.