Статья опубликована в рамках: XXXVIII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 29 октября 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ТЕПЛОФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРЕРЫВНОЙ ОТЛИВКИ
Омельченко Светлана Владимировна
канд. пед. наук, Южно-Уральский государственный университет, РФ, г. Челябинск
THERMOPHYSICAL MODELING OF CONTINUING CASTING
Svetlana Omelchenko
candidate of Pedagogic Sciences, South Ural State University, Russia, Chelyabinsk
АННОТАЦИЯ
Предлагается теплофизическая модель отливки металла при непрерывном литье в кристаллизаторе, учитывающая скорость движения заготовки, интенсивность теплообмена, физические свойства и геометрические параметры слитка.
ABSTRACT
A thermophysical model of metal casting in case of direct chill casting is offered considering base motion speed, heat-exchange rate, physical properties and geometrical parameters of a cast slab.
Ключевые слова: модель; отливка; теплофизика
Keywords: modeling; casting; thermal physics.
Создание новых и совершенствование существующих способов непрерывной разливки металла невозможны без теоретического исследования факторов, влияющих на стабильность и производительность процесса непрерывного литья.
В большинстве аналитических моделей [3; 5] рассматривается тепловое состояние отливок при циклическом (движение-остановка) извлечении заготовок из кристаллизаторов. Известные методики [2; 7] расчета затвердевания металла при непрерывном движении заготовки в кристаллизаторе также не отражают влияние скорости перемещения на тепловые процессы в отливке.
В настоящей работе предлагается математическая модель процессов, протекающих в непрерывно-литой заготовке с учетом ее движения с постоянной скоростью в кристаллизаторе, выделения скрытой теплоты плавления, охлаждающего действия кристаллизатора и других факторов.
Предполагается, что охлаждение металла происходит в цилиндрическом кристаллизаторе с металлической вставкой [6], интенсивность охлаждения не изменяется по длине кристаллизатора, основная часть теплоты кристаллизации ![]() выделяется в пределах жидкого ядра заготовки.
выделяется в пределах жидкого ядра заготовки.
При указанных предположениях процесс охлаждения поступающего из металлоприемника расплава описывается дифференциальным уравнением конвективной теплопроводности:3
|
|
(1) |
где: ![]() — температура,
— температура,
![]() ,
, ![]() — цилиндрические координаты,
— цилиндрические координаты,
![]() — коэффициент температуропроводности,
— коэффициент температуропроводности,
![]() — скорость движения заготовки,
— скорость движения заготовки,
![]() — функция объемных источников выделения теплоты
— функция объемных источников выделения теплоты ![]() .
.
В связи с уменьшением доли жидкого металла в отливке по длине кристаллизатора функцию ![]() представим выражением
представим выражением
|
|
(2) |
Здесь ![]() — плотность тепловыделения в начале координат,
— плотность тепловыделения в начале координат, ![]() ,
, ![]() — теплоемкость и плотность металла заготовки,
— теплоемкость и плотность металла заготовки, ![]() — длина жидкого ядра.
— длина жидкого ядра.
С другой стороны, функция ![]() связана со скрытой теплотой кристаллизации
связана со скрытой теплотой кристаллизации ![]() соотношением:
соотношением:
|
|
(3) |
где: ![]() — мощность тепловыделения при кристаллизации расплава,
— мощность тепловыделения при кристаллизации расплава,
![]() — массовая производительность линии литья,
— массовая производительность линии литья,
![]() — объем заготовки.
— объем заготовки.
Решая (3), получим формулу для плотности ![]() , используемую в дальнейших преобразованиях:
, используемую в дальнейших преобразованиях:
|
|
(4) |
Дифференциальное уравнение (1) решается при следующих условиях:
|
|
|
(5) |
Граничные условия отражают теплообмен между заготовкой и внутренней рабочей поверхностью кристаллизатора. Коэффициент теплообмена ![]() связан с теплоотдачей соотношением
связан с теплоотдачей соотношением ![]() , в котором
, в котором ![]() — коэффициент теплоотдачи,
— коэффициент теплоотдачи, ![]() — коэффициент теплопроводности материала отливки.
— коэффициент теплопроводности материала отливки.
Применяя методику решения дифференциальных уравнений в частных производных из [4], получим выражение для расчета температуры в отливке:
|
|
(6)
|
|
|
где ![]() ;
; ![]() ;
; 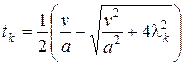 .
.
В этих выражениях ![]() ,
, ![]() — радиус заготовки,
— радиус заготовки, ![]() — корень уравнения, полученного из (5),
— корень уравнения, полученного из (5), ![]() ,
, ![]() — функции Бесселя нулевого и первого порядков.
— функции Бесселя нулевого и первого порядков.
Численные эксперименты по расчету температурных полей с помощью (6) проводились для непрерывно-литого слитка из чугуна. Диаметр заготовки составлял ![]() =2
=2![]() =0,1 м. Основные параметры технологического режима и свойства материала отливки (чугуна) заимствовались из [6]:
=0,1 м. Основные параметры технологического режима и свойства материала отливки (чугуна) заимствовались из [6]: ![]() =0,3 кг/с;
=0,3 кг/с; ![]() =0,2 м;
=0,2 м; ![]() =540 Дж/(м×°С);
=540 Дж/(м×°С); ![]() 7500 кг/м3;
7500 кг/м3; ![]() =2,3×105 Дж/кг;
=2,3×105 Дж/кг; ![]() =30 Вт/(м×°С);
=30 Вт/(м×°С); ![]() =7,4×10-6 м2/с; скорость вытягивания слитка из кристаллизатора в расчетах изменялась от
=7,4×10-6 м2/с; скорость вытягивания слитка из кристаллизатора в расчетах изменялась от ![]() =2×10-3 до 4×10-2 м/с; коэффициент теплоотдачи — от 625 до 10000 Вт/(м2×°С). Длина жидкого ядра
=2×10-3 до 4×10-2 м/с; коэффициент теплоотдачи — от 625 до 10000 Вт/(м2×°С). Длина жидкого ядра ![]() в заготовке уточнялась в каждом расчете и находилась в пределах 0,15 ¸ 3,0 м. Принималось также, что начальная температура расплава в металлоприемнике
в заготовке уточнялась в каждом расчете и находилась в пределах 0,15 ¸ 3,0 м. Принималось также, что начальная температура расплава в металлоприемнике ![]() =1200 °С, температура солидуса
=1200 °С, температура солидуса ![]() =1100 °С.
=1100 °С.
В силу приближенности модели на оси слитка расчеты показали заметное повышение температуры до ![]() »1290 °С (при
»1290 °С (при ![]() =0,005 м/с и
=0,005 м/с и ![]() =2500 Вт/(м2×°С)) вследствие подвода к металлу теплоты плавления. Однако, начиная с
=2500 Вт/(м2×°С)) вследствие подвода к металлу теплоты плавления. Однако, начиная с ![]() »0,03 м, это повышение незначительно, а при
»0,03 м, это повышение незначительно, а при ![]() =
=![]() =0,05 м не обнаруживается вовсе из-за интенсивного отвода тепла в стенку кристаллизатора. Область, где температура металла меньше температуры солидуса (
=0,05 м не обнаруживается вовсе из-за интенсивного отвода тепла в стенку кристаллизатора. Область, где температура металла меньше температуры солидуса (![]() =1100 °С), примем за зону затвердевшего расплава (корку). При данных условиях охлаждения толщина корки
=1100 °С), примем за зону затвердевшего расплава (корку). При данных условиях охлаждения толщина корки ![]() =
=![]() -
-![]() нарастает от нуля в начале кристаллизатора до 0,025 м на выходе из него. Здесь
нарастает от нуля в начале кристаллизатора до 0,025 м на выходе из него. Здесь ![]() — радиус внутренней поверхности корки.
— радиус внутренней поверхности корки.
В отличие от известных работ в настоящей модели исследуется роль скорости извлечения слитка из кристаллизатора в процессе затвердевания расплава. С увеличением скорости литья от 0,002 до 0,04 м/с длина жидкого ядра в отливке возрастает с 0,15 до 3,0 м при ![]() =2500 Вт/(м2×°С), а толщина корки металла на выходе из кристаллизатора уменьшается с 0,05 до 0,004 м.
=2500 Вт/(м2×°С), а толщина корки металла на выходе из кристаллизатора уменьшается с 0,05 до 0,004 м.
Выводы. Разработана теплофизическая модель охлаждения металла при непрерывном литье в кристаллизаторе. Модель связывает важнейшие технологические и теплофизические параметры формирования отливок: скорость извлечения заготовки из кристаллизатора, условия теплообмена между кристаллизирующимся металлом и рабочей поверхностью кристаллизатора, геометрию заготовки и физические свойства металла, включая скрытую теплоту плавления.
Список литературы:
1.Барановский Э.Ф. и др. Тепловые основы конструирования машин непрерывного литья свинцовой аккумуляторной решетки. // Литье и металлургия. — 2001. — № 2. — С. 60—64.
2.Гольдфарб Э.М. Теплотехника металлургических процессов. М.: Металлургия, 1967. — 439 с.
3.Капитонов В.С., Иванов А.А., Константинов В.С. Методика расчета затвердевания непрерывного слитка // Новое в создании металлургических машин. М.: 1985. С. 138 — с. 145.
4.Кошляков Н.С. и др. Уравнения в частных производных математической физики. М.: Высшая школа, 1970. — 712 с.
5.Марукович Е.И., Брановицкий А.М., Харьков В.А. Расчет затвердевания цилиндрической непрерывной отливки. // Литье и металлургия. — 2001. — № 2. — С. 25—29.
6.Специальные способы литья: Справочник / В.А. Ефимов, Г.А. Анисович, В.Н. Бабич и др. Под общей редакцией В.А. Ефимова. М.: Машиностроение, 1991. —736 с.
7.Урбанович Л.И. и др. Методика расчета температурного поля непрерывного слитка в кристаллизаторе. // ИФЖ. — 1976. — Том 31. — № 5 — С. 903.
дипломов


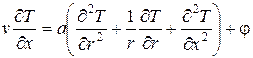 ,
,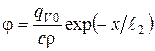 .
.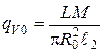 .
.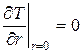 ;
; ;
;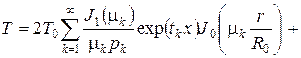
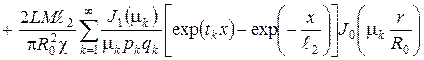 ,
,
Оставить комментарий